Gegeben ist das Rechteck . Punkte auf der Seite und Punkte auf der Seite legen zusammen mit dem Punkt Dreiecke fest. Die Winkel haben das Maß mit
Es gilt: ; .
Die Skizze zeigt das Dreieck für .
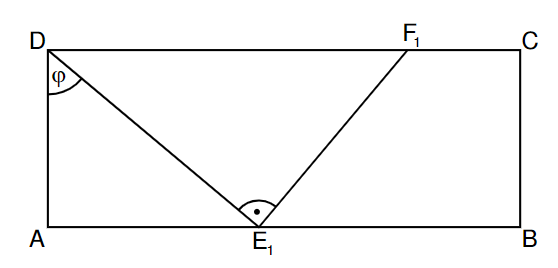
Begründen Sie, weshalb die Winkel stets das Maß haben
Zeigen Sie rechnerisch, dass für die Länge der Strecken in Abhängigkeit von gilt:
Berechnen Sie die Länge der Strecke . Runden Sie auf zwei Nachkommastellen.



