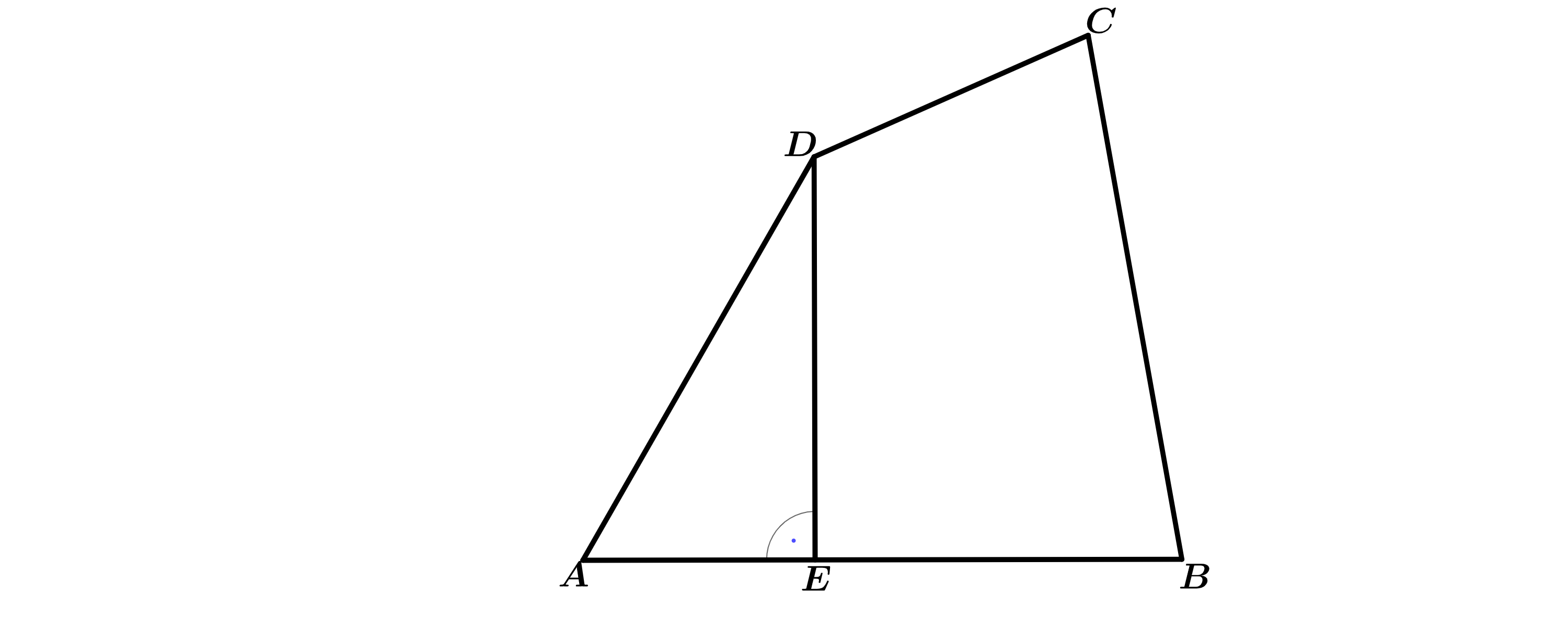
Die untenstehende Skizze zeigt den Plan eines Gartengrundstücks .
Es gilt: ; ;
; ; .
Runden Sie im Folgenden auf eine Stelle nach dem Komma.

Zeichnen Sie das Viereck im Maßstab .
Die dreieckige Gartenfläche die im Plan durch die Strecken und begrenzt ist, soll geschottert werden. Eine Metallschiene, im Plan durch gekennzeichnet, soll verhindern, dass sich der Schotter im ganzen Grundstück verteilt. Zum Nachbargrundstück wird entlang der im Plan durch gekennzeichneten Strecke ein Sichtschutz errichtet. Berechnen Sie die Länge der Strecken und .
[Teilergebnis: ]
Die im Plan durch das Viereck dargestellte Fläche soll aus einem Rasenstück und einem Beet bestehen.
Bestimmen Sie rechnerisch die Länge der Strecke [EC] sowie den Flächeninhalt des Vierecks .
[Ergebnis: ; Teilergebnis: ]
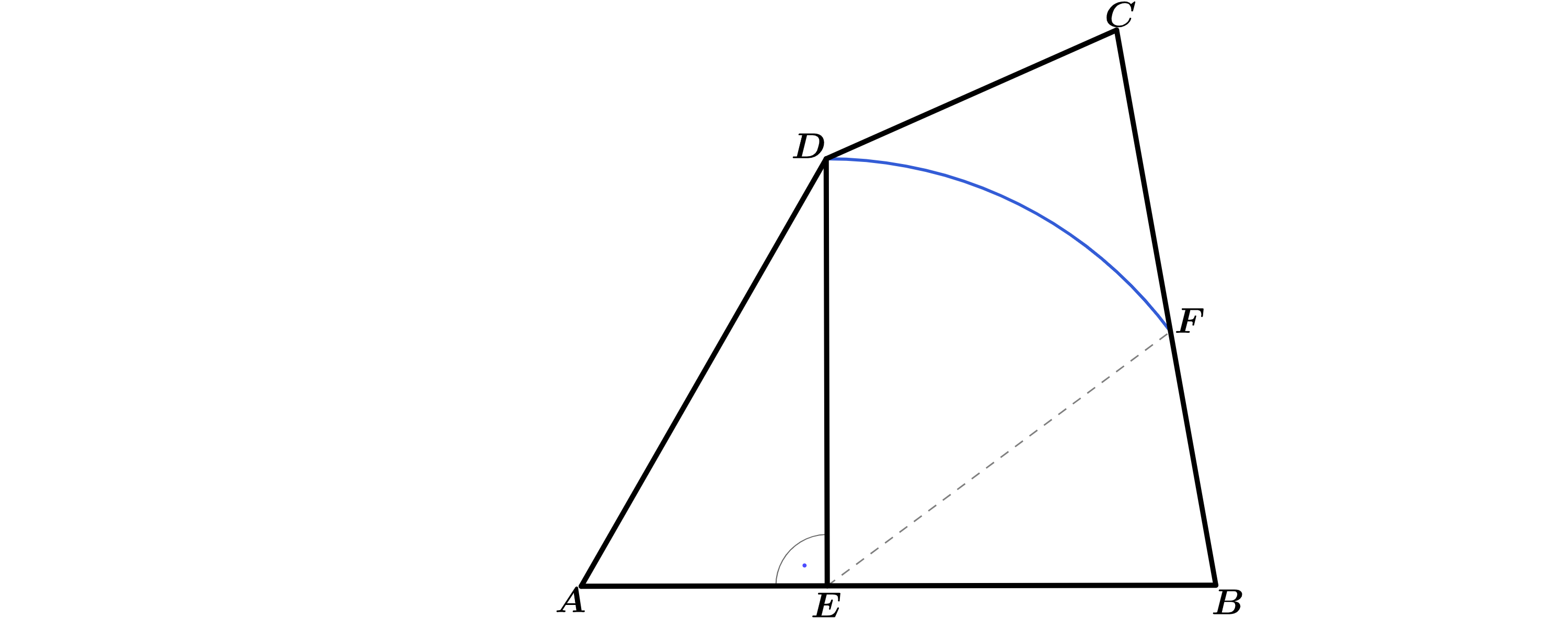
Der Kreis mit dem Mittelpunkt E hat den Radius und schneidet die Strecke [BC] im Punkt F. Das Beet wird durch den Kreisbogen sowie durch die Strecken und begrenzt. Zeichnen Sie den Kreisbogen in die Zeichnung zur Teilaufgabe (a) ein.
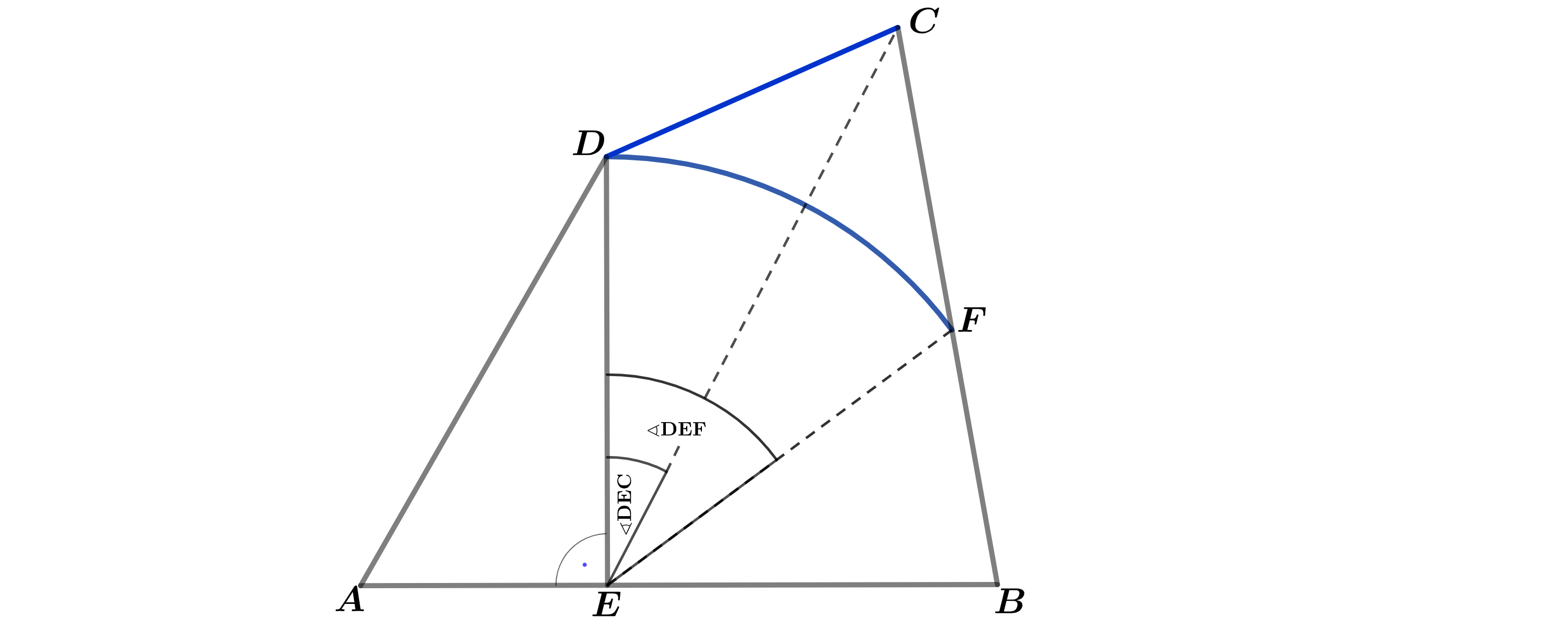
Das Beet aus Teilaufgabe (d) wird entlang des Kreisbogens und der Strecke [DC] mit einem Schneckenschutzzaun geschützt. Berechnen Sie die benötigte Länge des Zauns.
[Teilergebnis: ]
Berechnen Sie den Flächeninhalt des Beetes.