Aufgabe B1
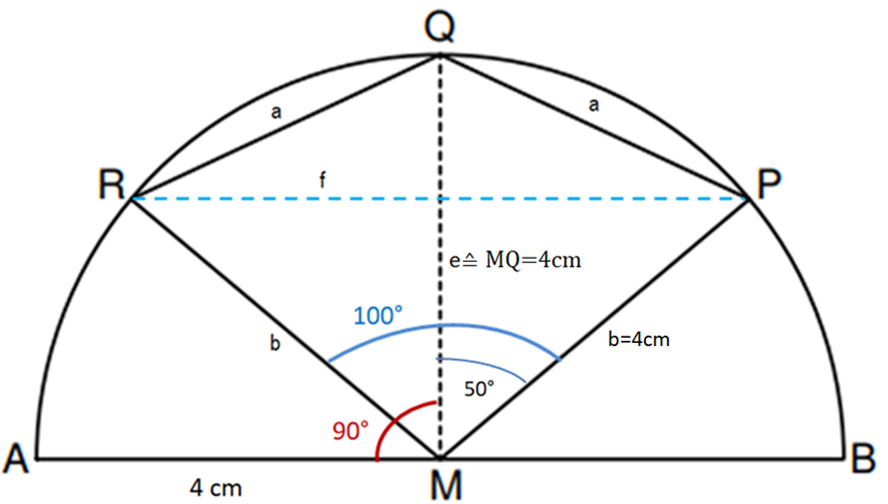
Der Punkt ist der Mittelpunkt der Strecke und des Kreisbogens . Die Punkte und liegen auf dem Kreisbogen und bilden zusammen mit dem Punkt das Drachenviereck mit der Symmetrieachse (siehe Skizze).
Es gilt: ; .
Runden Sie auf zwei Stellen nach dem Komma.
Zeichnen Sie die Strecke , den Kreisbogen sowie das Drachenviereck . (2 P)
Berechnen Sie den Umfang des Drachenvierecks . (2 P)
Ergebnis:
Berechnen Sie den prozentualen Anteil des Umfangs des Drachenvierecks am Umfang der Figur, die sich aus dem Kreisbogen sowie der Strecke zusammensetzt. (2 P)