Springe zum Inhalt oder Footer
SerloDie freie Lernplattform
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.

In der folgenden Abbildung gilt:

AB‾∣∣A′B′‾;BC‾∣∣B′C′‾;CA‾∣∣C′A′‾\mathrm{\overline{AB}||\overline{A'B'};\quad\overline{BC}||\overline{B'C'};\quad\overline{CA}||\overline{C'A'}}

Bild

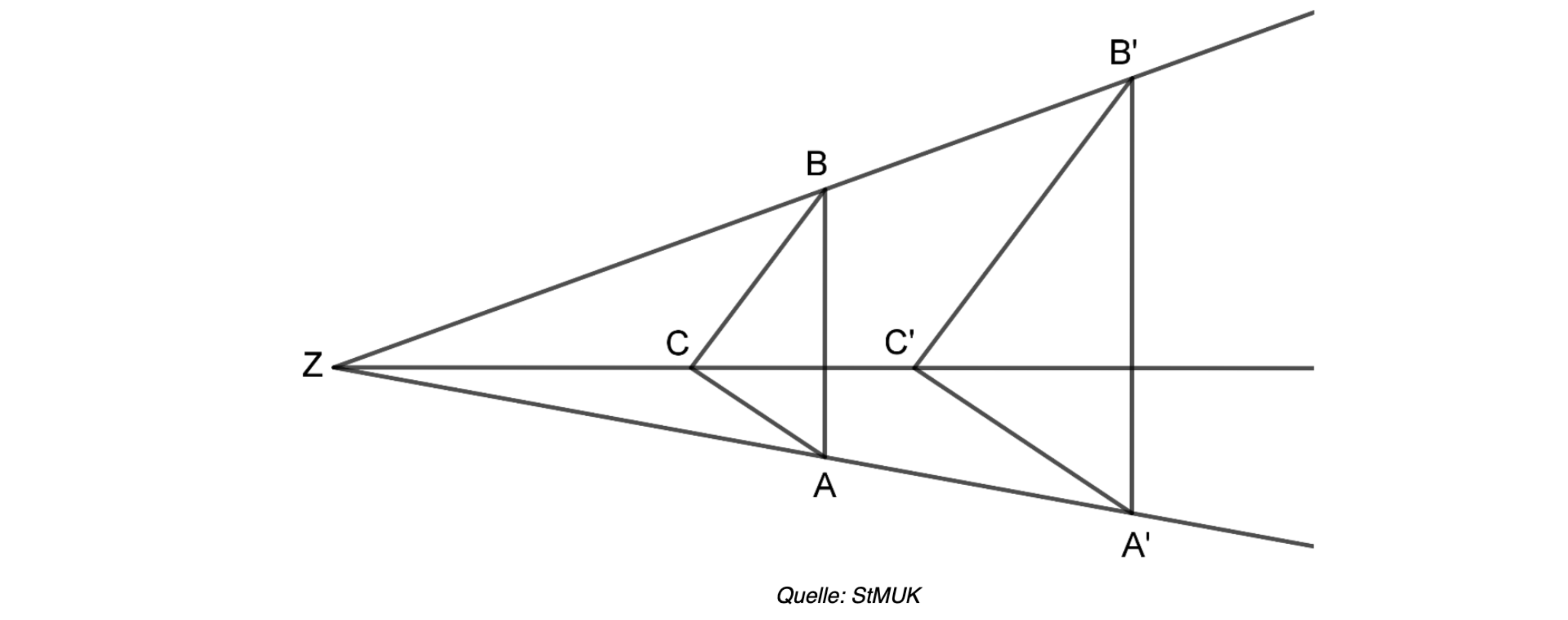
Schreiben Sie die folgenden Aussagen auf Ihr Lösungsblatt und ergänzen Sie

jeweils die Platzhalter □\square{} so, dass die drei Gleichungen richtig sind.

(I)∣ZA‾∣□=□∣A′B′‾∣(II)□∣AA′‾∣=∣ZB‾∣□(III)∣ZC‾∣∣CB‾∣=□□\mathrm{(I)\quad\dfrac{|\overline{ZA}|}{\square{}}=\dfrac{\square}{|\overline{A'B'}|}\qquad\qquad(II)\quad\dfrac{\square}{|\overline{AA'}|}=\dfrac{|\overline{ZB}|}{\square{}}\qquad\qquad(III)\quad\dfrac{|\overline{ZC}|}{|\overline{{CB}}|}=\dfrac{\square{}}{\square{}}}