Teil B- Aufgabengruppe II
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier sind die originalen Prüfungsaufgaben zu finden.
- 1
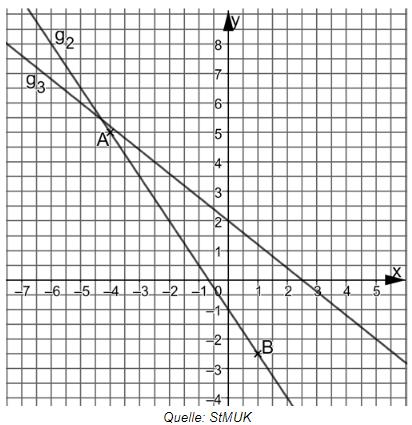
Die folgende Abbildung zeigt denGraphen der Geraden :
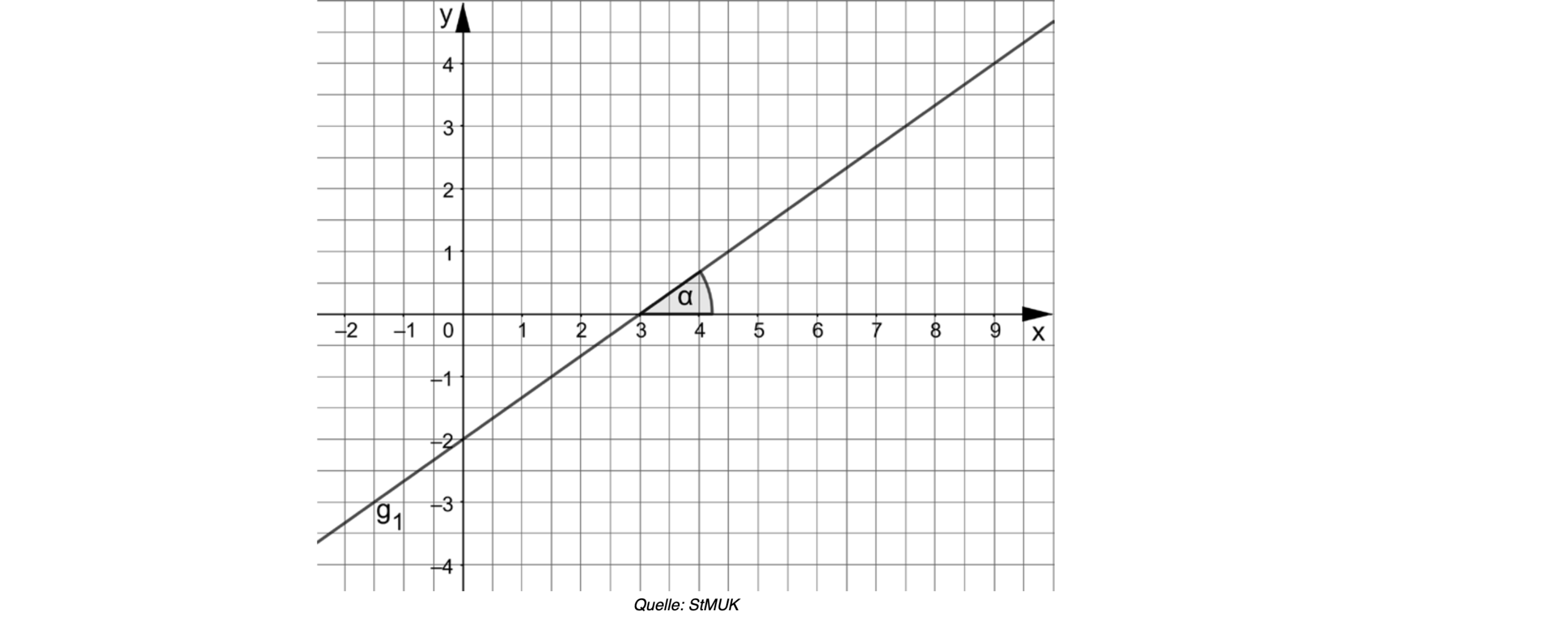
Geben Sie die Funktionsgleichung der Geraden an.
Berechnen Sie den Winkel , den die Gerade mit der -Achse einschließt
(siehe Abbildung).
Die Gerade verläuft durch die Punkte und .
Bestimmen Sie rechnerisch die Funktionsgleichung von .
Die Gerade : steht senkrecht auf der Geraden , die durch den Ursprung verläuft.
Bestimmen Sie die Funktionsgleichung von .
ist der Schnittpunkt der Geraden mit der -Achse.
Ermitteln Sie rechnerisch die -Koordinate des Punktes und geben Sie
diesen Punkt an.
Die Gerade hat die Funktionsgleichung
Zeigen Sie nachvollziehbar, dass der Schnittpunkt der Geraden mit der
Geraden auf der -Achse liegt.
Zeichnen Sie die Geraden und in ein Koordinatensystem mit der
Längeneinheit .
- 2
Lösen Sie die folgende Gleichung rechnerisch.
Geben Sie die Definitionsmenge und die Lösungsmenge an.
- 3
Das Alter von archäologischen Knochenfunden kann über die Masse des
vorhandenen radioaktiven Kohlenstoffisotops bestimmt werden.
Die Halbwertszeit für das Kohlenstoffisotop beträgt Jahre.
Berechnen Sie die Masse an , die bei einer Ausgangsmasse von
Gramm nach Jahren noch vorhanden ist.
In einem gefundenen Knochen befinden sich noch Milligramm des Kohlenstoffisotops . Wissenschaftler bestimmen das Alter des Knochens auf Jahre.
Bestimmen Sie rechnerisch die Masse des ursprünglich vorhandenen Kohlenstoffisotops .
Im Lonetal wurde der Knochen eines Mammuts gefunden. Der Anteil des
radioaktiven Kohlenstoffisotops ist zum Zeitpunkt der Untersuchung
bereits auf gesunken.
Berechnen Sie das Alter des Knochens.
- 4
Ein Pralinenhersteller fertigt Kugeln aus weißer Schokolade an, die mit Nougat
gefüllt sind. Der Außendurchmesser dieser Kugeln beträgt zwei Zentimeter, die
Wandstärke aus weißer Schokolade Millimeter.
Ein Kubikzentimeter des Nougats hat eine Masse von Gramm.
Berechnen Sie die Masse der Nougatfüllung, die für die Herstellung
von Kugeln benötigt wird.
Berechnen Sie das Volumen der weißen Schokolade, das für die Herstellung
von Kugeln benötigt wird.
Damit das Nougat nicht durch die weiße Schokolade dringen kann, wird die
Innenwand der Hohlkugel aus weißer Schokolade mit einer Zuckerlösung bestrichen.
Berechnen Sie den Inhalt der zu bestreichenden Fläche einer Hohlkugel.
- 5
Bei einer Gleichung zur Anwendung einer binomischen Formel ist nur das
gemischte Glied bekannt.
Stellen Sie eine mögliche vollständige Gleichung auf und notieren Sie diese auf
Ihrem Lösungsblatt.
- 6
Berechnen Sie die Höhe der Pyramide mit quadratischer Grundfläche
(siehe Skizze).
Es gilt:
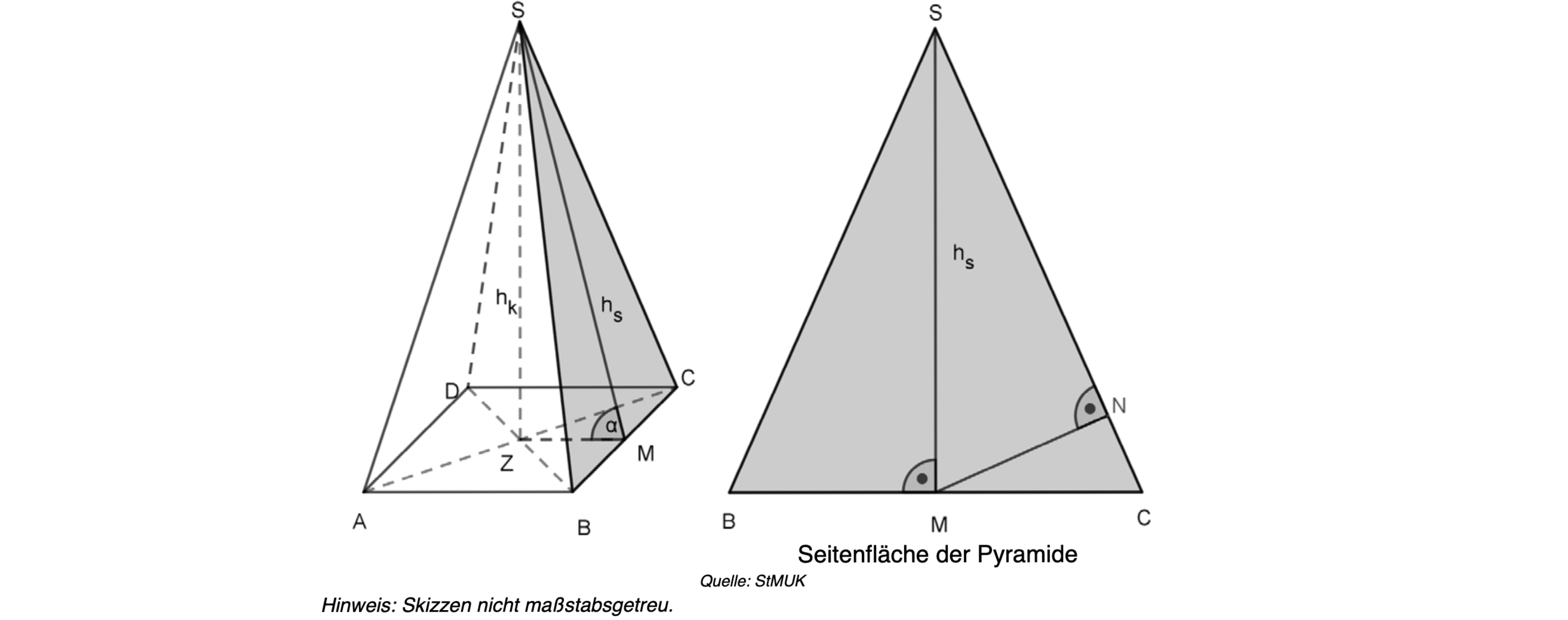
- 7
Lösen Sie die folgenden Aufgaben.
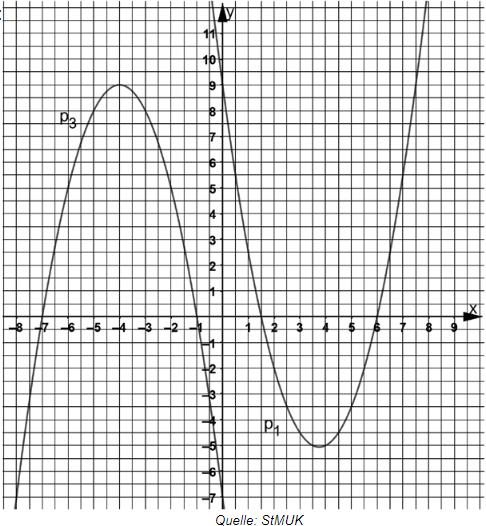
Eine nach oben geöffnete Normalparabel schneidet die -Achse in den
Punkten und .
Ermitteln Sie rechnerisch die Normalform der Parabel .
Eine weitere Parabel hat den Scheitelpunkt .
Bestimmen Sie rechnerisch die Koordinaten von .
Die Parabel wird an der -Achse gespiegelt.
Dadurch entsteht die Parabel .
Ermitteln Sie rechnerisch die Funktionsgleichung von in der Normalform.
Bestimmen Sie rechnerisch die Schnittpunkte und der Parabel mit
der -Achse und geben Sie diese an.
Zeichnen Sie die Parabeln und in ein Koordinatensystem mit der
Längeneinheit
Die Parabel hat die Funktionsgleichung , die Parabel die
Funktionsgleichung .
Begründen Sie nachvollziehbar, dass die Parabeln und keinen Schnittpunkt haben.
- 8
Eine Hardrockband plant Konzerte in Deutschland.
Für jedes Konzert gewinnen zwei Besucher mit ihrer Eintrittskarte ein Treffen mit der Band.
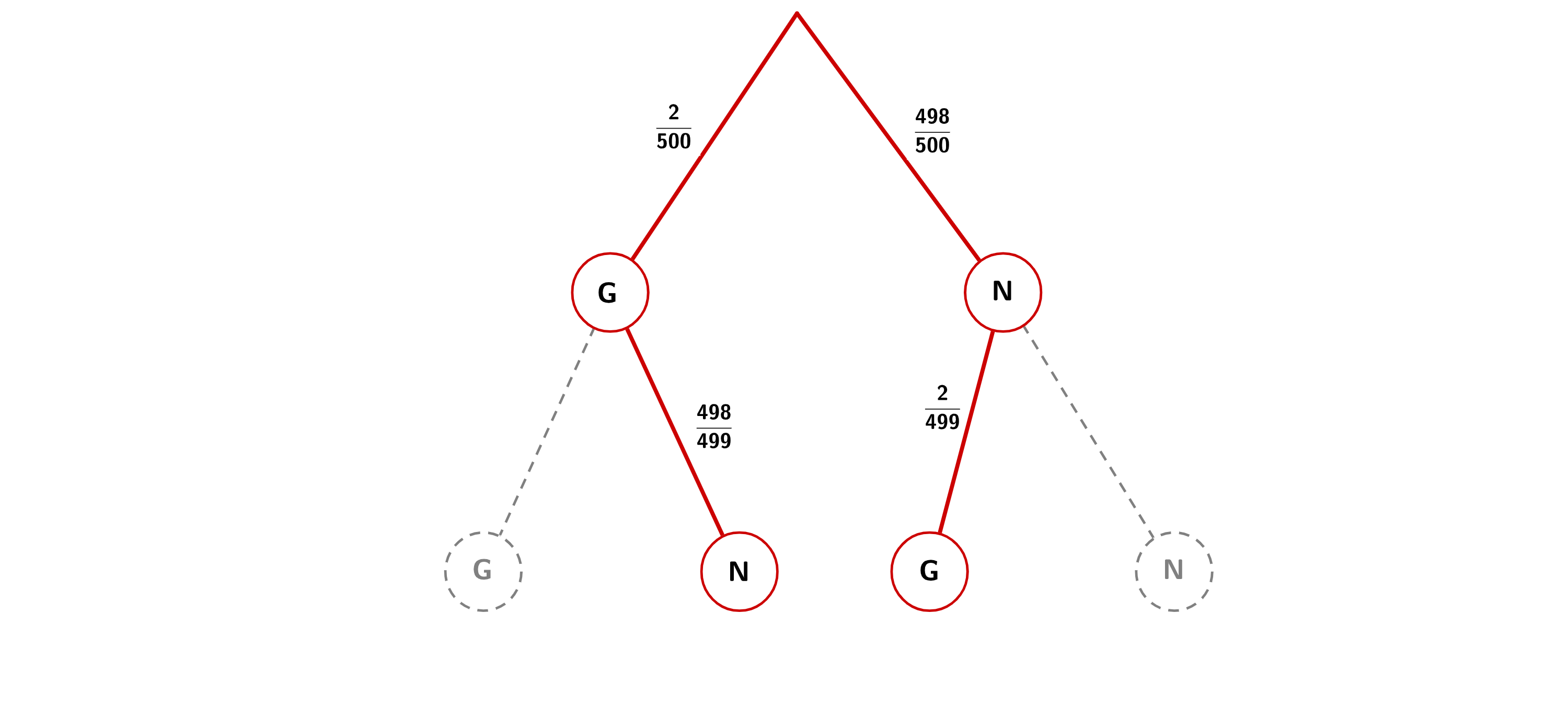
Für das erste Konzert gibt es 500 Eintrittskarten. Berechnen Sie die Wahrscheinlichkeit, dass beim Verkauf der ersten beiden Eintrittskarten genau eine Gewinnerkarte verkauft wird.
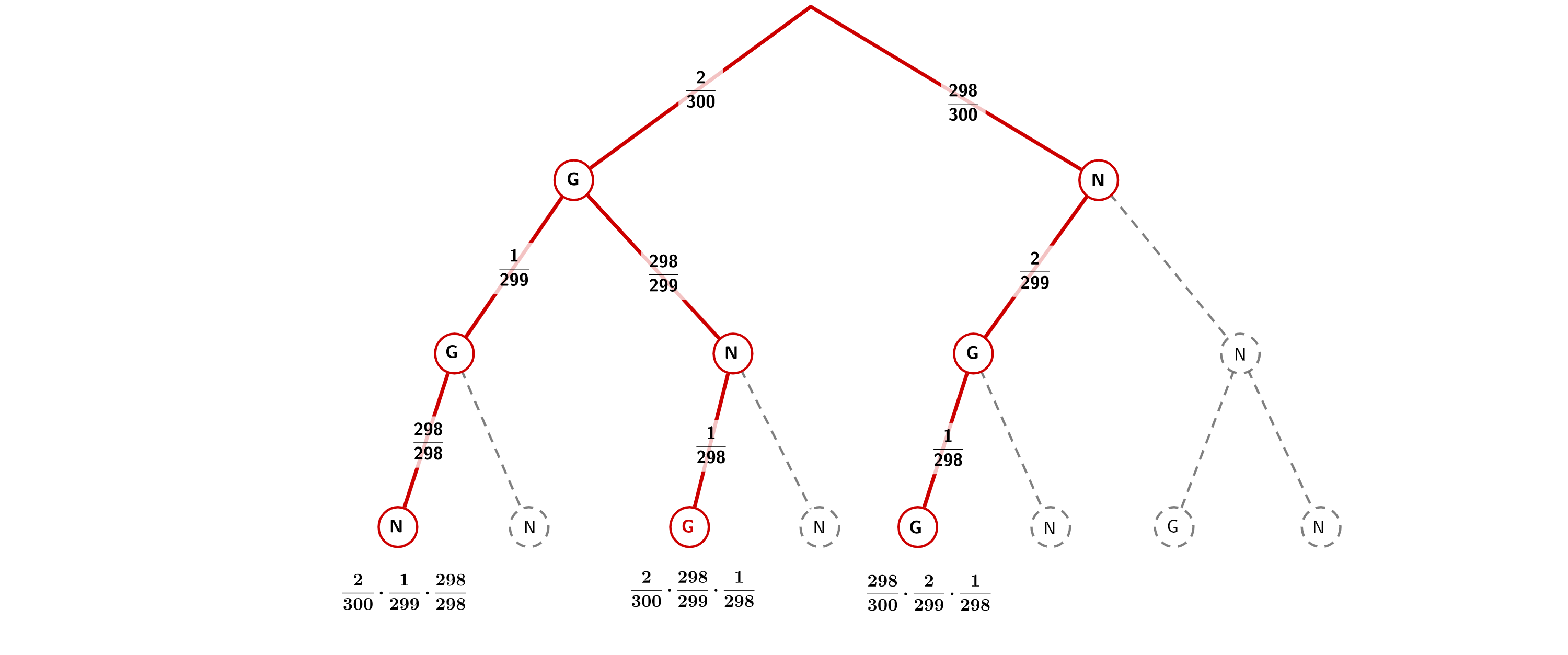
Nach dem Verkauf der ersten von den Eintrittskarten für das erste Konzert sind beide Gewinnerkarten noch nicht verkauft.
Ermitteln Sie rechnerisch die Wahrscheinlichkeit, dass beim Verkauf der nächsten drei Karten beide Gewinnerkarten dabei sind.
In Frankreich plant die Band zehn weitere Konzerte. Diese sollen in zehn verschiedenen Städten stattfinden.
Berechnen Sie die Anzahl der Kombinationsmöglichkeiten für die Auswahl der ersten drei Städte.
- 9
In der folgenden Abbildung gilt:
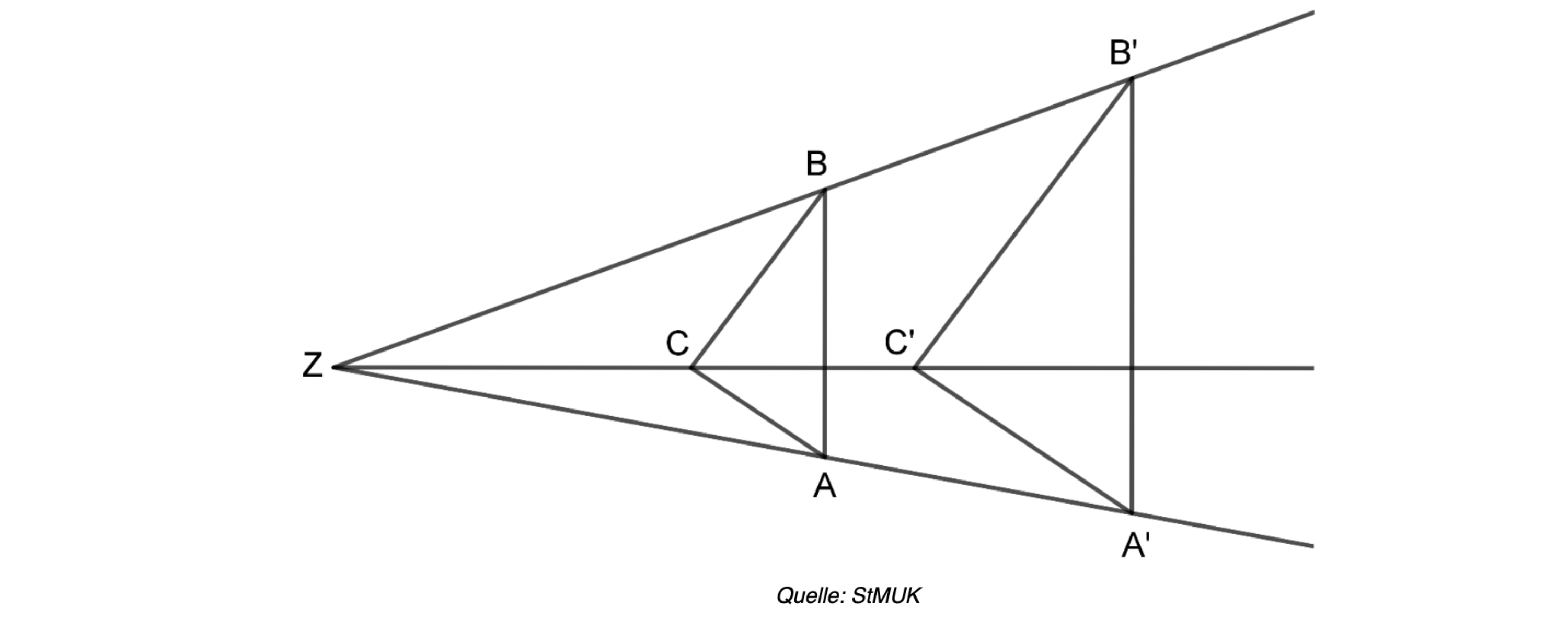
Schreiben Sie die folgenden Aussagen auf Ihr Lösungsblatt und ergänzen Sie
jeweils die Platzhalter so, dass die drei Gleichungen richtig sind.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?