Die folgende Abbildung zeigt denGraphen der Geraden :
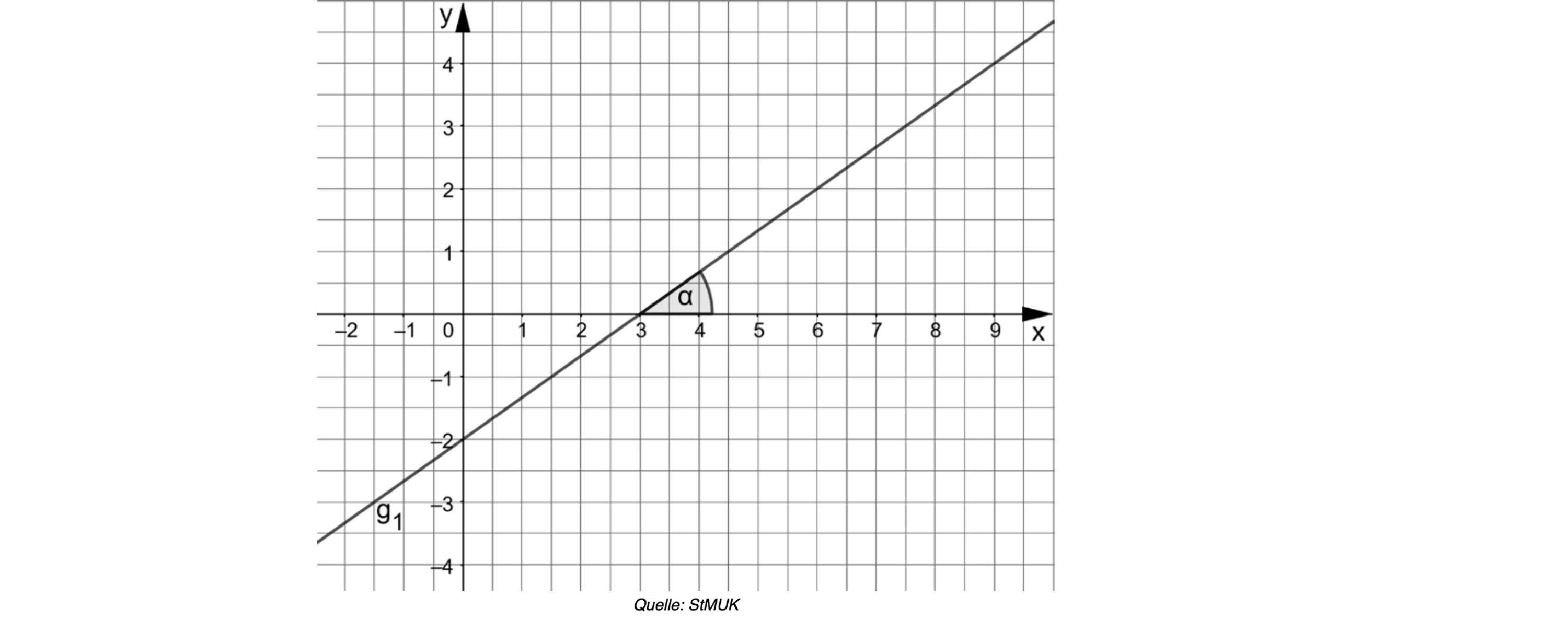
Geben Sie die Funktionsgleichung der Geraden an.
Berechnen Sie den Winkel , den die Gerade mit der -Achse einschließt
(siehe Abbildung).
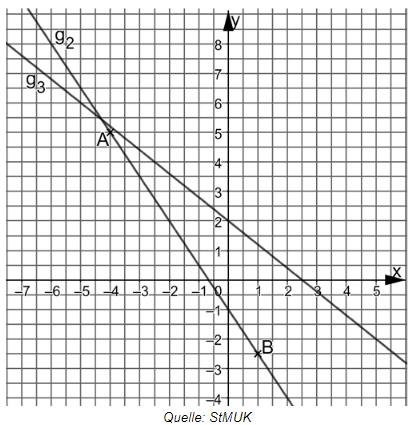
Die Gerade verläuft durch die Punkte und .
Bestimmen Sie rechnerisch die Funktionsgleichung von .
Die Gerade : steht senkrecht auf der Geraden , die durch den Ursprung verläuft.
Bestimmen Sie die Funktionsgleichung von .
ist der Schnittpunkt der Geraden mit der -Achse.
Ermitteln Sie rechnerisch die -Koordinate des Punktes und geben Sie
diesen Punkt an.
Die Gerade hat die Funktionsgleichung
Zeigen Sie nachvollziehbar, dass der Schnittpunkt der Geraden mit der
Geraden auf der -Achse liegt.
Zeichnen Sie die Geraden und in ein Koordinatensystem mit der
Längeneinheit .