Als Teilnehmer eines Auswahlverfahrens zur Einstellung von Werkstudenten bei einer großen
Molkerei wird Ihnen folgende Aufgabe gestellt:
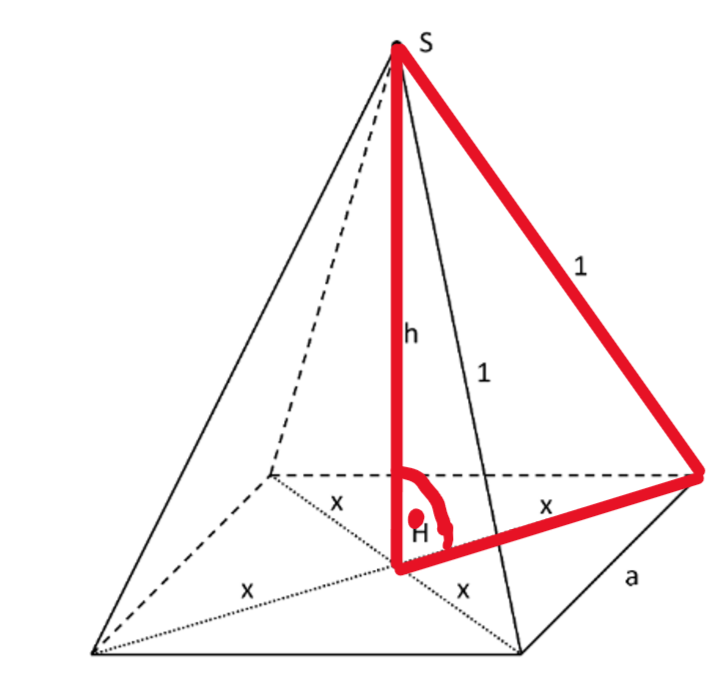
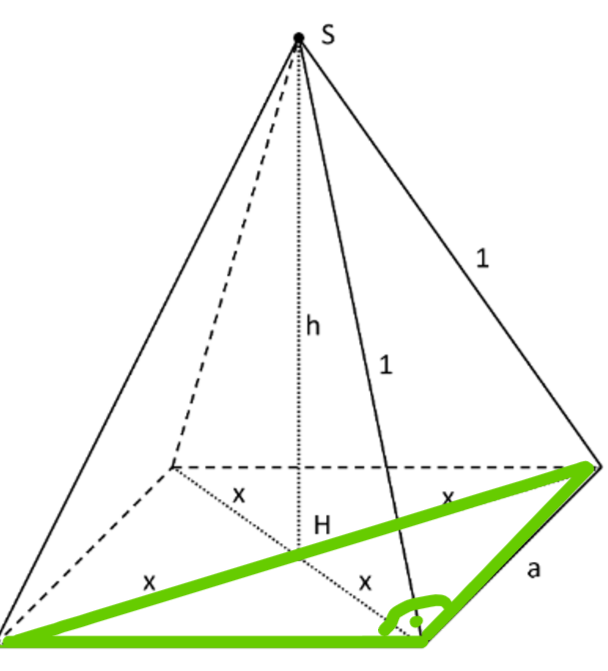
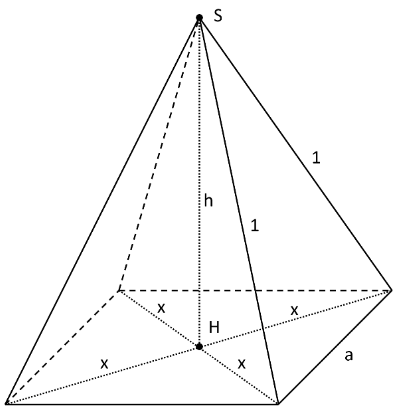
Ein Schokodrink soll in einem Tetra Pak abgefüllt werden, welcher die Form einer geraden Pyramide mit quadratischer Grundfläche hat. Die vier Seitenkanten der Pyramide sollen aus verpackungstechnischen Gründen jeweils eine feste Länge von 1 dm haben.
Die Spitze S der Pyramide liegt senkrecht über dem Punkt H, in dem sich die Diagonalen der Grundfläche im rechten Winkel schneiden.
Aus verkaufstechnischen Gründen soll die Höhe des Tetra Paks mindestens 0,4 dm und höchstens 0,6 dm betragen.
Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.
Stellen Sie eine Gleichung der Funktion auf. Dabei steht h für die Höhe der Pyramide in dm und für das Volumen der Pyramide in .
[Mögliches Teilergebnis: ] (4 BE)
Bestimmen Sie unter den oben genannten Vorgaben, für welche Höhe h der Tetra Pak den maximalen Rauminhalt aufweist. Berechnen Sie dieses maximale Volumen. Runden Sie Ihre Ergebnisse auf zwei Nachkommastellen. (7 BE)