Teil 2, Analysis II

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellungen zum Ausdrucken findest du hier

Gegeben ist die Funktion f durch $f(x)=\frac 1 {12}(x^4-20x^2+64)$ mit der Definitionsmenge $D_f=[-3;4{,}5]$ sowie die lineare Funktion $g:y=\frac {15}4$ mit der Definitionsmenge $D_g=\mathbb R$ .

Die Graphen der Funktion f und g in einem kartesischen Koordinatensystem werden mit $G_f$ bzw. $G_g$ bezeichnet.

Geben Sie an, ob die folgende Aussage wahr oder falsch ist, und begründen Sie Ihre Entscheidung.
"Der Graph der Funktion f ist auf $D_f$ achsensymmetrisch zur y-Achse." (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich
Da nur gerade Exponenten für x vorkommen und somit $f(-x)=f(x)$ gilt, könnte man meinen, dass der Graph achsensymmetrisch ist.
Allerdings ist dies aufgrund der Definitionsmenge nicht der Fall: Der Bereich rechts vom Ursprung ist größer als der links vom Ursprung (bis 4,5 bzw bis -3) und somit ist der Graph nicht symmetrisch, da links ein Teil "weggeschnitten" ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Hier genügt es nicht, den Funktionsterm zu untersuchen und damit Symmetrie festzustellen.
Stattdessen musst du die eingeschränkte Definitionsmenge mit in deine Überlegungen einbeziehen.

Berechnen Sie die Nullstellen der Funktion f. (5 BE)

Bestimmen Sie Art und Koordinaten sämtlicher Extrempunkte von $G_f$ und geben Sie die Wertemenge $W_f$ der Funktion an. (8 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertemenge

Randextrema

Da beide Ränder der Definitionsmenge $D_f=[-3;4{,}5]$ eingeschlossen sind, gibt es zwei Randextrema, deren y-Koordinaten du wie gewohnt durch Einsetzen in den Funktionsterm erhältst:

$R_1(-3|f(-3)) \Rightarrow R_1(-3|-\frac{35}{12})$ und

$R_2(4{,}5|f(4{,}5)) \Rightarrow R_2(4{,}5|\frac{1105}{192})$

Ob es sich dabei um Randhoch- oder Tiefpunkte handelt, kannst du erst entscheiden, nachdem du die anderen Extremstellen bzw. das Monotonieverhalten untersucht hast.

Extremstellen bestimmen

Bestimme die erste Ableitung von $f(x)=\frac 1 {12}(x^4-20x^2+64)$ :

$f'(x)=\frac{1}{12}\left(4x^3-40x\right)$

Bestimme nun die Nullstellen der Ableitungsfunktion, um die Kandidaten für Extremstellen zu finden:

$\displaystyle f'\left(x\right)$	$=$	$\displaystyle 0$
$\displaystyle \frac{1}{12}\left(4x^3-40x\right)$	$=$	$\displaystyle 0$
	↓	Klammere 4x aus
$\displaystyle \frac{1}{3}x\left(x^2-10\right)$	$=$	$\displaystyle 0$

Der Satz vom Nullprodukt besagt, dass ein Produkt immer dann 0 ist, wenn mindestens ein Faktor 0 ist. Der Faktor $\frac{1}{3}$ ist nie 0. Unterscheide deshalb:

$x=0$ und $x^2-10=0$

Der erste Faktor liefert direkt die erste Nullstelle $x_1=0$

Untersuche $x^2-10=0$ weiter:

$\displaystyle x^2-10$	$=$	$\displaystyle 0$	$\displaystyle +10$
$\displaystyle x^2$	$=$	$\displaystyle 10$
	↓	Ziehe die Wurzel. Beachte, dass es zwei Lösungen gibt.
$\displaystyle x_2$	$=$	$\displaystyle \sqrt{10}\approx3{,}16$
$\displaystyle x_3$	$=$	$\displaystyle -\sqrt{10}\approx-3{,}16$

Da $x_3<-3$ ist diese Nullstelle nicht in der Definitionsmenge und deshalb nicht weiter interessant.

Bestimme die Art aller Extremstellen, z.B. über die Monotonietabelle:

x	-3	<x<	0	<x<	$\sqrt{10}$	<x<	4,5
$f'(x)$		+	0	-	0	+
$G_f$	Rand- TIP (da danach $\nearrow)$	$\nearrow$	HOP	$\searrow$	TIP	$\nearrow$	Rand- HOP (da davor $\nearrow)$

Bestimme vom Hochpunkt bei $x=0$ und vom Tiefpunkt bei $x=\sqrt{10}$ die y-Koordinaten durch Einsetzen in f:

$f\left(0\right)=\frac{16}{3}$ , also $HOP\left(0|\frac {16}3\right)$

$f(\sqrt{10})=-3$ , also $TIP(\sqrt{10}|-3)$

und bereits berechnet: $R_1(-3|-\frac{35}{12})$ und $R_2(4{,}5|\frac{1105}{192})$

Wertemenge angeben

Wähle nun den kleinsten und den größten y-Wert aller Extrempunkte für die Wertemenge aus.

Als Hilfestellung: $\frac{16}3\approx 5{,}33$ , $-\frac{35}{12}\approx-2{,}92$ und $\frac{1105}{192}\approx5{,}76$

Der kleinste y-Wert ist also beim Tiefpunkt $TIP\left(\sqrt{10}|-3\right)$ und der größte y-Wert beim Randhochpunkt $R_2\left(4{,}5\ |\frac{1105}{192}\right)$ :

$W_f=[-3;\frac{1105}{192}]$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

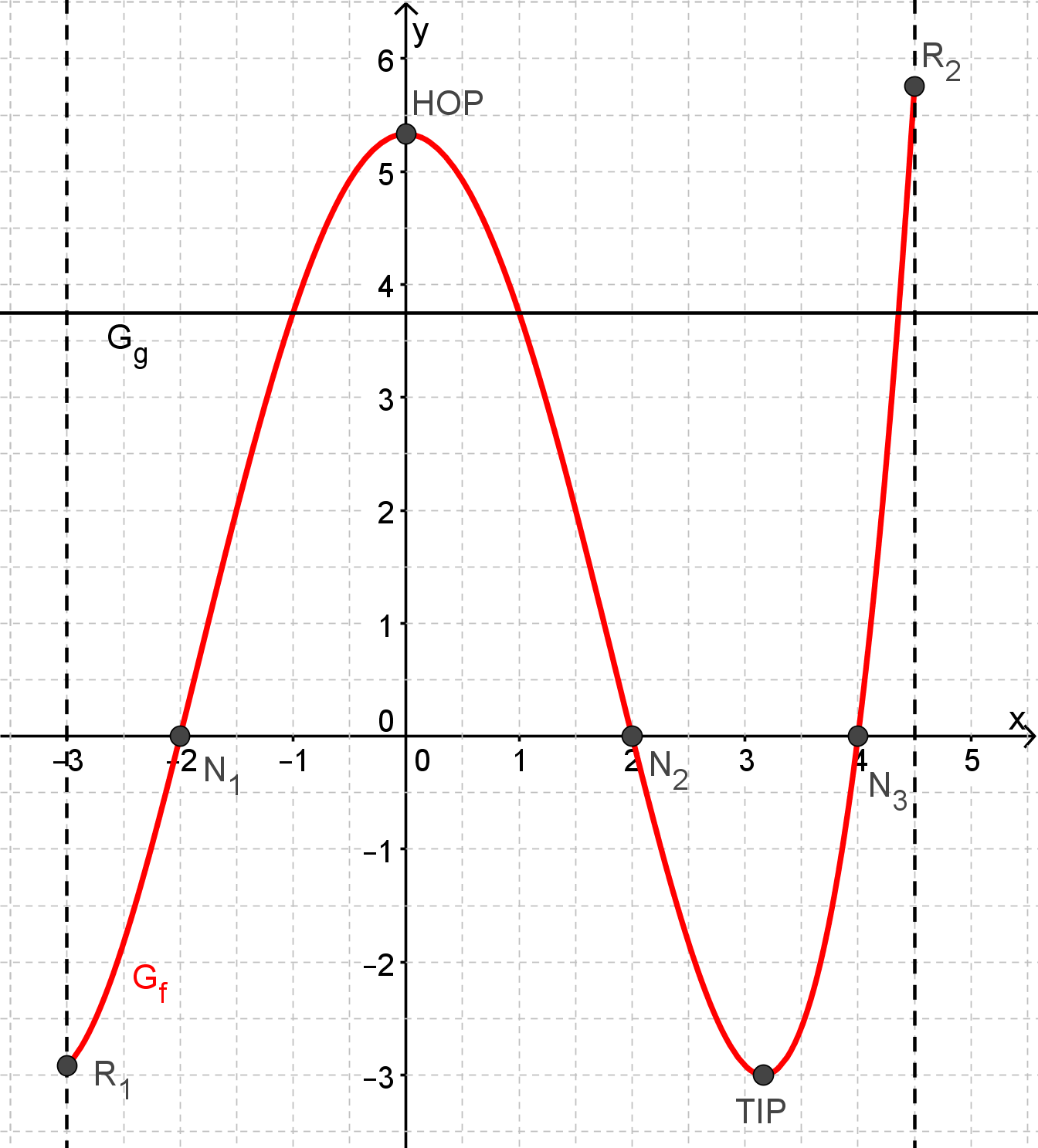
Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse den Graphen $G_f$ und die Gerade $G_g$ in ein kartesisches Koordinatensystem.
Maßstab für beide Achsen: $1\ LE\ =1\ cm$ (5 BE)
Die Zeichnung mit der Wertetabelle ist ein guter Moment, um deine bisher berechneten Ergebnisse zu überprüfen!
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Beachte die gegebene Definitions- und die soeben berechnete Wertemenge beim Zeichnen des Koordinatensystems.
Starte zunächst durch die Markierung der Definitionsmenge durch senkrechte, gestrichelte Linien. Zeichne nicht über diese Linien hinaus!
Da du die Funktion zeichnen sollst, fertige eine Wertetabelle für den gegebenen Definitionsbereich an und markiere dann die Punkte.
Gehe anschließend von oben nach unten durch alle Teilaufgaben und markiere berechnete Punkte.
Im ersten Angabentext war auch von der Gerade g die Rede, zeichne diese ebenfalls ein.

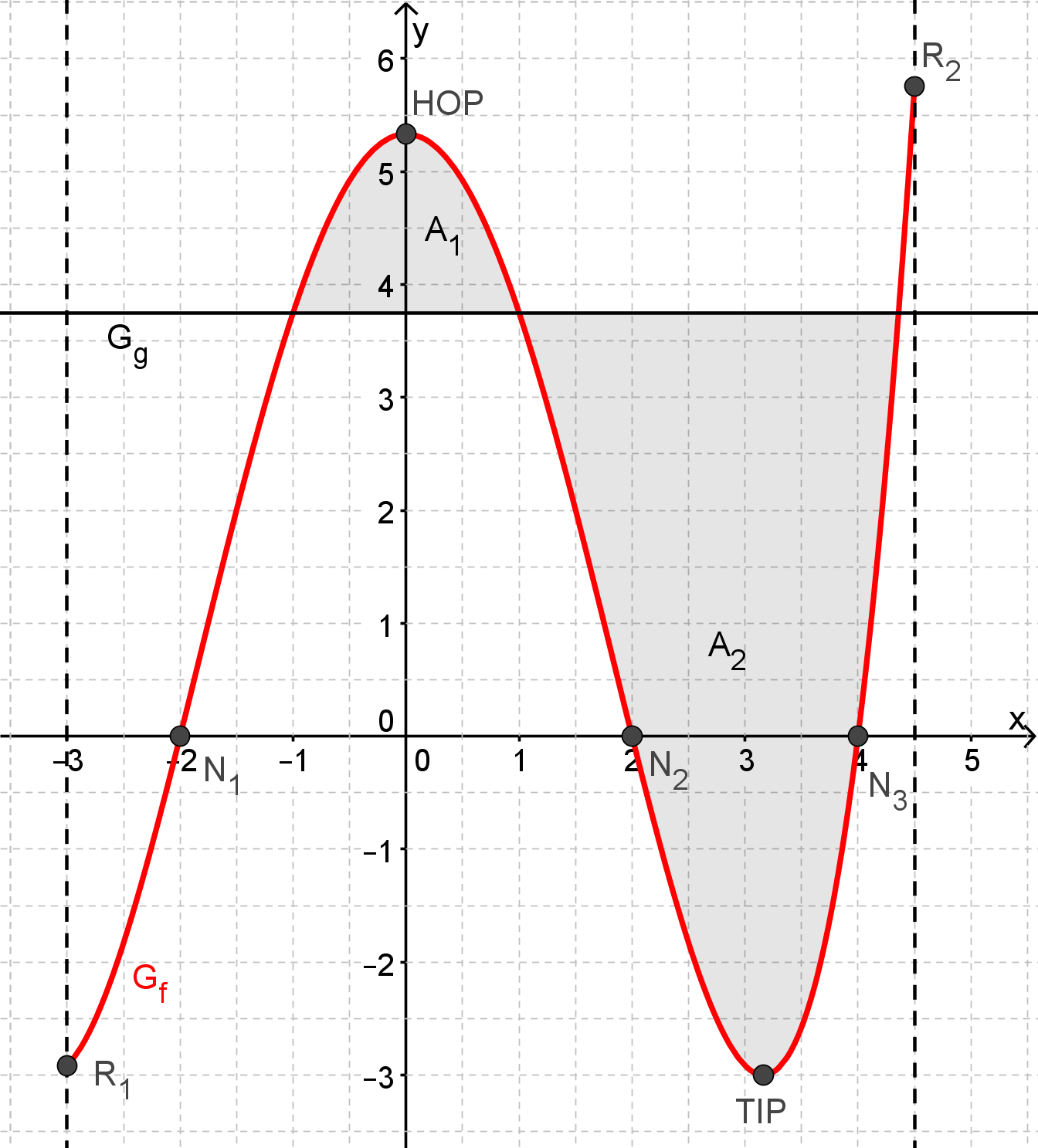
Die Graphen der beiden Funktionen f und g schneiden sich an den Stellen $x_1=-1$ , $x_2=1$ und $x_3=\sqrt{19}$ (Nachweis nicht erforderlich) und schließen somit zwei endliche Flächenstücke ein. Berechnen Sie die Maßzahl des Flächeninhalts des kleineren der beiden Flächenstücke. Runden Sie Ihr Ergebnis auf zwei Nachkommastellen. (4 BE)

Als Teilnehmer eines Auswahlverfahrens zur Einstellung von Werkstudenten bei einer großen

Molkerei wird Ihnen folgende Aufgabe gestellt:

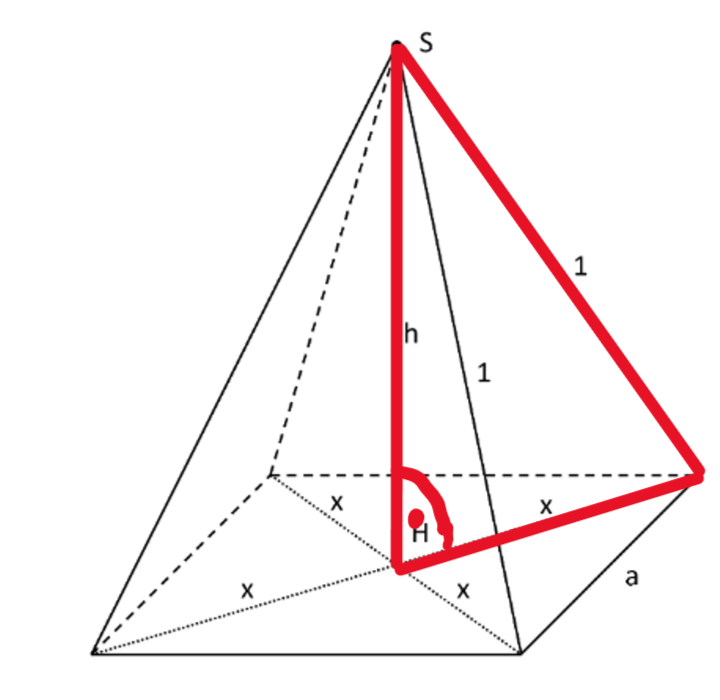
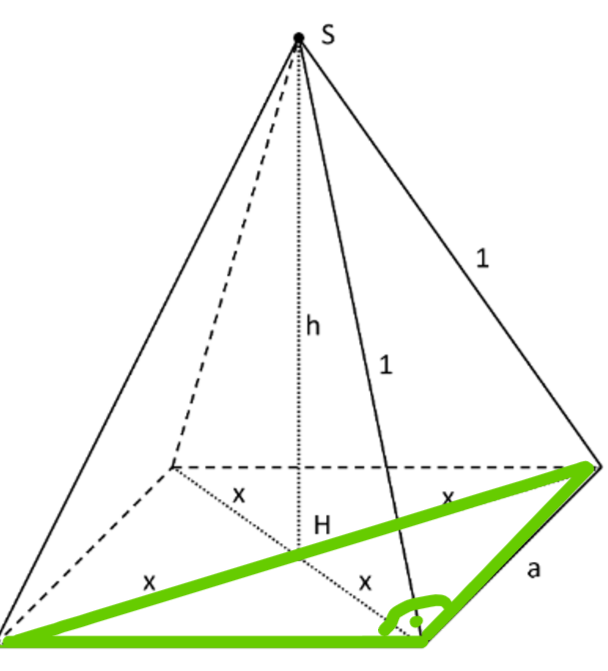
Ein Schokodrink soll in einem Tetra Pak abgefüllt werden, welcher die Form einer geraden Pyramide mit quadratischer Grundfläche hat. Die vier Seitenkanten der Pyramide sollen aus verpackungstechnischen Gründen jeweils eine feste Länge von 1 dm haben.

Die Spitze S der Pyramide liegt senkrecht über dem Punkt H, in dem sich die Diagonalen der Grundfläche im rechten Winkel schneiden.

Aus verkaufstechnischen Gründen soll die Höhe des Tetra Paks mindestens 0,4 dm und höchstens 0,6 dm betragen.

Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.

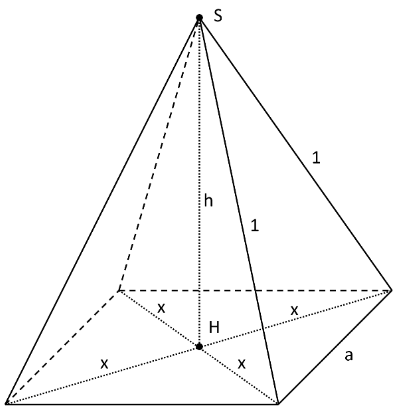
Stellen Sie eine Gleichung der Funktion $V:h\mapsto V(h)$ auf. Dabei steht h für die Höhe der Pyramide in dm und $V(h)$ für das Volumen der Pyramide in $dm^3$ .

[Mögliches Teilergebnis: $V(h)=-\frac 2 3h^3+\frac 2 3 h$ ] (4 BE)

Bestimmen Sie unter den oben genannten Vorgaben, für welche Höhe h der Tetra Pak den maximalen Rauminhalt aufweist. Berechnen Sie dieses maximale Volumen. Runden Sie Ihre Ergebnisse auf zwei Nachkommastellen. (7 BE)

90% einer Rasenfläche sind vermoost. Das Moos soll mit einem umweltverträglichen Mittel zurückgedrängt werden. Die zeitliche Entwicklung der vom Moos bedeckten Rasenfläche wird näherungsweise mittels der Modellfunktion M mit der Funktionsgleichung $M(t)=a\cdot e^{bt}$ mit $t\in \mathbb{R}^+_0$ und $a,b \in \mathbb{R}\backslash\{0\}$ beschrieben. Dabei steht die Variable t für die Zeit in Tagen ab dem Zeitpunkt $t_0=0$ der Ausbringung des Mittels. Der jeweilige Funktionswert von M gibt die

gesamte mit Moos bedeckte Fläche in $m^2$ zum Zeitpunkt t an. Bekannt ist, dass zwei Tage nach Ausbringung des Mittels noch $400m^2$ und nach neun Tagen nur noch $140m^2$ vermoost sind.

Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.

Bestimmen Sie die Werte der Parameter a und b. Runden Sie a ganzzahlig und b auf zwei Nachkommastellen. Berechnen Sie die Maßzahl des Flächeninhalts der Rasenfläche. (5 BE)

Für die folgende Teilaufgabe gilt: $a=540; b=-0{,}15$
Der Hersteller des umweltverträglichen Mittels wirbt damit, dass die mit Moos bedeckte Fläche nach der Ausbringung innerhalb einer Woche um ca. 65% zurückgehen wird. Überprüfen Sie diese Werbeaussage, indem Sie berechnen, nach wie vielen Tagen diese Reduzierung laut dem Modell aus 3.0 erreicht wird. Runden Sie auf ganze Tage.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialgleichung
Wenn die Bemoosung um ca $65\%$ zurückgeht, sind nach einer Woche noch $100\%-65\%=35\%$ vorhanden.
Da die prozentuale Zu- oder Abnahme beim exponentiellen Wachstum unabhängig vom Startwert ist, musst du, wenn du mit Prozenten rechnest, die 540 in der folgenden Rechnung weglassen:
$0{,}35=e^{-0{,}15t}$
Wende den ln an:
$\ln(0{,}35)=-0{,}15t$
und somit $t=\dfrac{\ln(0{,}35)}{-0{,}15}\approx 7$
Die Werbeaussage trifft also annähernd zu
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme zunächst, wie viel Prozent des Rasens nach einer Woche noch bemoost sein sollen. Ignoriere dann den Startwert und bestimme durch Umformen mithilfe des Logaritmus die benötigte Zeit.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

	$\displaystyle s\left(x\right)$
$=$	$\displaystyle f\left(x\right)-g\left(x\right)$
$=$	$\displaystyle \frac{1}{12}\left(x^4-20x^2+64\right)-\frac{15}{4}$
$=$	$\displaystyle \frac{1}{12}x^4-\frac{5}{3}x^2+\frac{19}{12}$

$\displaystyle \int_{-1}^1s\left(x\right)dx$	$=$	$\displaystyle \int_{-1}^1\left(\frac{1}{12}x^4-\frac{5}{3}x^2+\frac{19}{12}\right)dx$
	↓	Bilde eine Stammfunktion S(x) von s(x)
	$=$	$\displaystyle \left[\frac{1}{60}x^5-\frac{5}{9}x^3+\frac{19}{12}x\right]_{-1}^1$
	↓	Setze 1 und -1 in diese Stammfunktion ein, subtrahiere die Ergebnisse
	$=$	$\displaystyle S\left(1\right)-S\left(-1\right)$
	$=$	$\displaystyle \frac{94}{45}$

$\displaystyle 2a^2$	$=$	$\displaystyle 4x^2$	$\displaystyle :4$
$\displaystyle \frac{1}{2}a^2$	$=$	$\displaystyle x^2$
	↓	Ersetze in der Nebenbedingung $h^2+x^2=1$ von oben das $x^2$ :
$\displaystyle h^2+\frac{1}{2}a^2$	$=$	$\displaystyle 1$	$\displaystyle -h^2$
$\displaystyle 0{,}5a^2$	$=$	$\displaystyle 1-h^2$	$\displaystyle \cdot2$
$\displaystyle a^2$	$=$	$\displaystyle 2-2h^2$

$\displaystyle V'\left(x\right)$	$=$	$\displaystyle 0_{ }$
$\displaystyle -2x^2+\frac{2}{3}$	$=$	$\displaystyle 0$	$\displaystyle +2x^2$
$\displaystyle \frac{2}{3}$	$=$	$\displaystyle 2x^2$	$\displaystyle :2$
$\displaystyle \frac{1}{3}$	$=$	$\displaystyle x^2$
	↓	Ziehe die Wurzel. Beachte, dass es zwei Lösungen gibt.
$\displaystyle x_1$	$≈$	$\displaystyle 0{,}58$
$\displaystyle x_2$	$≈$	$\displaystyle -0{,}58$

Forme die linke Seite um
	↓
$\displaystyle \frac{e^{9b}}{e^{2b}}\cdot400$	$=$	$\displaystyle 140$	$\displaystyle :400$
	↓	Verwende links die Potenzgesetze.
$\displaystyle e^{9b-2b}$	$=$	$\displaystyle \frac{7}{20}$
$\displaystyle e^{7b}$	$=$	$\displaystyle \frac{7}{20}$
	↓	Verwende den natürlichen Logarithmus
$\displaystyle \ln\left(\frac{7}{20}\right)$	$=$	$\displaystyle 7b$	$\displaystyle :7$
$\displaystyle b$	$≈$	$\displaystyle -0{,}15$

Teil 2, Analysis II

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Randextrema

Extremstellen bestimmen

Wertemenge angeben

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Flächenstück markieren

Differenzfunktion bilden

Wert des bestimmten Integrals berechnen

Hast du eine Frage oder Feedback?

Pyramidenvolumen

Nebenbedingung über feste Kantenlänge

Nebenbedingung in Hauptbedingung einsetzen

Hast du eine Frage oder Feedback?

Definitionsmenge

Kandidaten für Extremstellen

Funktionswerte an Extremstellen und Rändern

Hast du eine Frage oder Feedback?

Parameter a und b bestimmen

Größe des Rasens

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

$\displaystyle f\left(x\right)$	$=$	$\displaystyle 0$
$\displaystyle \frac{1}{12}\left(x^4-20x^2+64\right)$	$=$	$\displaystyle 0$	$\displaystyle :\frac{1}{12}$
	↓	Die $\frac 1 {12}$ haben keinen Einfluss auf die Nullstellen (Satz vom Nullprodukt)
$\displaystyle x^4-20x^2+64$	$=$	$\displaystyle 0$

$\displaystyle u_1$	$=$	$\displaystyle 4$
	↓	verwende $u=x^2$
$\displaystyle x^2$	$=$	$\displaystyle 4$
	↓	Ziehe die Wurzel. Vergiss nicht, dass es zwei Lösungen gibt!
$\displaystyle x_1$	$=$	$\displaystyle 2$
$\displaystyle x_2$	$=$	$\displaystyle -2$

$\displaystyle u_2$	$=$	$\displaystyle 16$
	↓	verwende $u=x_{ }^2$
$\displaystyle x^2$	$=$	$\displaystyle 16$
	↓	Ziehe die Wurzel.
$\displaystyle x_3$	$=$	$\displaystyle 4$
$\displaystyle x_4$	$=$	$\displaystyle -4$