Wahlteil - GTR - lernen mit Serlo!

Aufgabe 3B

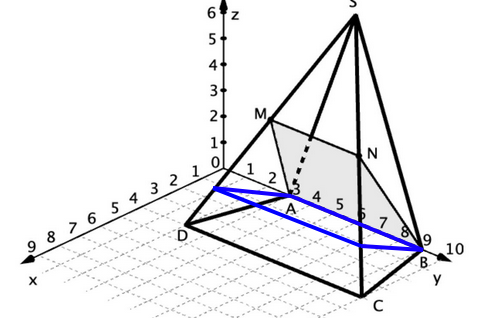
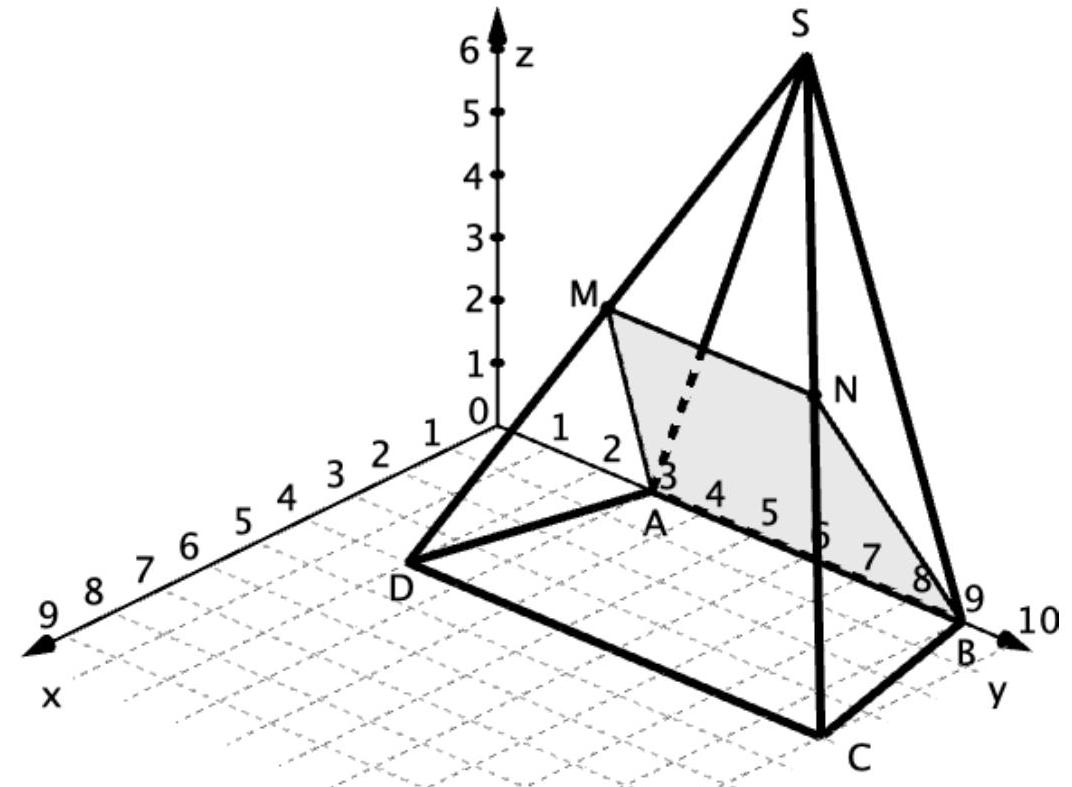
Die Abbildung zeigt die Pyramide $A B C D S$ mit

$A (0 | 3 | 0), B (0 | 9 | 0), C (4 | 10 | 0)$ und $D (4 | 2 | 0)$ sowie der Spitze im Punkt $S (0 | 6 | 8)$ .

$M$ bezeichnet den Mittelpunkt der Kante $D S$ und $N$ bezeichnet den Mittelpunkt der Kante $C S$ .

Begründen Sie, dass das Dreieck $D C S$ gleichschenklig ist.
Bestimmen Sie eine Gleichung für die Gerade, auf der die Symmetrieachse des Dreiecks DCS liegt. (6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie
Gleichschenkliges Dreieck
Die Seiten $D S$ und $C S$ müssen gleich lang sein, damit das Dreieck gleichschenklig ist. Wir überprüfen:
$\vec{D S} = \vec{O S} - \vec{O D} = (\begin{array}{c} 0 \\ 6 \\ 8 \end{array}) - (\begin{array}{c} 4 \\ 2 \\ 0 \end{array}) = (\begin{array}{c} - 4 \\ 4 \\ 8 \end{array})$
$\vec{C S} = \vec{O S} - \vec{O C} = (\begin{array}{c} 0 \\ 6 \\ 8 \end{array}) - (\begin{array}{c} 4 \\ 10 \\ 0 \end{array}) = (\begin{array}{c} - 4 \\ - 4 \\ 8 \end{array})$
Die Beträge der Koordinaten sind gleich, weshalb die Vektoren gleich lang sind. Das Dreieck ist damit gleichschenklig.
Geradengleichung aufstellen
Die Mitte der beiden Punkte $C (4 | 10 | 0)$ und $D (4 | 2 | 0)$ ist der Punkt $M_{C D} (4 | 6 | 0)$ . Die Geradengleichung durch die Spitze und $M_{C D}$ lautet:
$g : \vec{x}$ $=$ $\vec{O S} + t \cdot \vec{S M_{C S}}$
$=$ $(\begin{array}{c} 0 \\ 6 \\ 8 \end{array}) + t \cdot (\begin{array}{c} 4 - 0 \\ 6 - 6 \\ 0 - 8 \end{array})$
$=$ $(\begin{array}{c} 0 \\ 6 \\ 8 \end{array}) + t \cdot (\begin{array}{c} 4 \\ 0 \\ - 8 \end{array})$
Wobei der Parameter $t \in ℝ$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zeige, dass die Seiten $D S$ und $C S$ gleich lang sind.
Bestimme den Mittelpunkt der Strecke $D C$ und stelle eine Geradengleichung durch $S$ und diesen Mittelpunkt auf.
Berechnen Sie den von den Kanten $A B$ und $A M$ eingeschlossenen Winkel. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen Vektoren, Geraden und Ebenen
Punkt $M$
Die Mitte der Punkte $S (0 | 6 | 8)$ und $D (4 | 2 | 0)$ ist der Punkt $M (2 | 4 | 4)$ . Hier wurde jeweils die Mitte der Koordinaten bestimmt.
Vektoren berechnen
Die Vektoren $\vec{A B}$ und $\vec{A M}$ berechnen wir "Spitze minus Fuß":
$\vec{A B}$ $=$ $\vec{O B} - \vec{O A} = (\begin{array}{c} 0 \\ 9 \\ 0 \end{array}) - (\begin{array}{c} 0 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} 0 \\ 6 \\ 0 \end{array})$
$\vec{A M}$ $=$ $\vec{O M} - \vec{O A} = (\begin{array}{c} 2 \\ 4 \\ 4 \end{array}) - (\begin{array}{c} 0 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} 2 \\ 1 \\ 4 \end{array})$
Die Länge der Vektoren, die wir für den Winkel benötigen, betragen:
$| \vec{A B} |$ $=$ $\sqrt{0^{2} + 6^{2} + 0^{2}} = 6$
$| \vec{A M} |$ $=$ $\sqrt{2^{2} + 1^{2} + 4^{2}} = \sqrt{21}$
Winkel berechnen
Wir setzen die Vektoren und deren Längen in die Formel ein:
$\cos α$ $=$ $\frac{\vec{a} \cdot \vec{b}}{| \vec{a} | \cdot | \vec{b} |}$
$=$ $\frac{(\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) \cdot (\begin{array}{c} 2 \\ 1 \\ 4 \end{array})}{6 \cdot \sqrt{21}}$
$=$ $\frac{6}{6 \cdot \sqrt{21}}$ $\cos^{- 1} ()$
$α$ $\approx$ $77 °$
Der Winkel zwischen den Vektoren beträgt etwa $77 °$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme die Koordinaten des Punktes $M$ .
Bestimme die Vektoren $\vec{A B}$ und $\vec{A M}$ .
Berechne den Winkel zwischen den Vektoren mit der Formel: $\cos α = \frac{\vec{a} \cdot \vec{b}}{| \vec{a} | \cdot | \vec{b} |}$
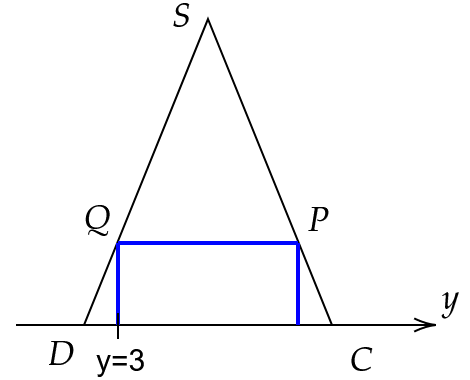
Die Punkte $A, B, M$ und $N$ sind die Eckpunkte eines Trapezes.
Betrachtet wird jetzt ein beliebiger Punkt $P$ auf der Kante $C S$ sowie ein beliebiger Punkt $Q$ auf der Kante $D S$ .
Begründen Sie, dass die Punkte $P$ und $Q$ die folgenden Koordinaten haben: (5 BE)
$P (4 - 4 p | 10 - 4 p | 8 p)$ mit $0 \leq p \leq 1$
$Q (4 - 4 q | 2 + 4 q | 8 q)$ mit $0 \leq q \leq 1$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie
Geraden aufstellen
Gerade durch $C$ und $S$ : $\vec{x} = \vec{O C} + p \cdot \vec{C S} = (\begin{array}{c} 4 \\ 10 \\ 0 \end{array}) + p \cdot (\begin{array}{c} 0 - 4 \\ 6 - 10 \\ 8 - 0 \end{array}) = (\begin{array}{c} 4 \\ 10 \\ 0 \end{array}) + p \cdot (\begin{array}{c} - 4 \\ - 4 \\ 8 \end{array})$
Gerade durch $D$ und $S$ : $\vec{x} = \vec{O D} + p \cdot \vec{D S} = (\begin{array}{c} 4 \\ 2 \\ 0 \end{array}) + p \cdot (\begin{array}{c} 0 - 4 \\ 6 - 2 \\ 8 - 0 \end{array}) = (\begin{array}{c} 4 \\ 2 \\ 0 \end{array}) + p \cdot (\begin{array}{c} - 4 \\ 4 \\ 8 \end{array})$
Punkte aufstellen
Die Parameter $p \in ℝ$ beschreiben für $0 \leq p \leq 1$ Punkte zwischen $C / D$ und $S$ .
Die Zeilen der Geraden werden als Koordinaten aufgeschrieben:
$P (4 - 4 p | 10 - 4 p | 8 p)$ mit $0 \leq p \leq 1$
$Q (4 - 4 q | 2 + 4 q | 8 q)$ mit $0 \leq q \leq 1$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme die Geraden durch die Punkte $C$ und $S$ , sowie durch $D$ und $S$ .
Schreibe die Zeilen der Geraden als Koordinaten auf.
Untersuchen Sie, ob es einen Punkt $P$ sowie einen Punkt $Q$ gibt, sodass das Viereck $A B P Q$ ein Rechteck ist. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
Nachweis des Rechtecks
In der Skizze lässt sich sehen, dass es so einen Fall geben muss. Die Vektoren $\vec{B P}$ und $\vec{A Q}$ stehen dabei senkrecht auf der y-Achse.
Von vorne lässt sich das leichter erkennen:
Wenn der Punkt $Q$ die y-Koordinate $3$ hat, steht die Seite senkrecht auf der y-Achse.
Dazu muss gelten: $2 + 4 q = 3$
Die Lösung $q = \frac{1}{4}$ existiert, daher gibt es so einen Punkt $Q (3 | 3 | 2)$ .
Genauso erhält man für den Vektor $\vec{B P}$ , dass die $y$ -Koordinate den Wert $9$ haben muss: $10 - 4 p = 9$ ergibt auch $p = \frac{1}{4}$ . Damit existiert auch $P (3 | 9 | 2)$ .
Da der Abstand $| \vec{P Q} | = 6 = | \vec{A B} |$ ist, handelt es sich wirklich um ein Rechteck.
Pyramide von vorne
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für ein Rechteck müssen alle Innenwinkel $90 °$ betragen.
Bestimme den Parameter $p$ der Punkte $P$ und $Q$ auf Teilaufgabe (c), für die die Vektoren senkrecht auf der y-Achse stehen.

Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen → Was bedeutet das?

$g : \vec{x}$	$=$	$\vec{O S} + t \cdot \vec{S M_{C S}}$
	$=$	$(\begin{array}{c} 0 \\ 6 \\ 8 \end{array}) + t \cdot (\begin{array}{c} 4 - 0 \\ 6 - 6 \\ 0 - 8 \end{array})$
	$=$	$(\begin{array}{c} 0 \\ 6 \\ 8 \end{array}) + t \cdot (\begin{array}{c} 4 \\ 0 \\ - 8 \end{array})$

$\vec{A B}$	$=$	$\vec{O B} - \vec{O A} = (\begin{array}{c} 0 \\ 9 \\ 0 \end{array}) - (\begin{array}{c} 0 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} 0 \\ 6 \\ 0 \end{array})$
$\vec{A M}$	$=$	$\vec{O M} - \vec{O A} = (\begin{array}{c} 2 \\ 4 \\ 4 \end{array}) - (\begin{array}{c} 0 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} 2 \\ 1 \\ 4 \end{array})$

$\| \vec{A B} \|$	$=$	$\sqrt{0^{2} + 6^{2} + 0^{2}} = 6$
$\| \vec{A M} \|$	$=$	$\sqrt{2^{2} + 1^{2} + 4^{2}} = \sqrt{21}$

$\cos α$	$=$	$\frac{\vec{a} \cdot \vec{b}}{\| \vec{a} \| \cdot \| \vec{b} \|}$
	$=$	$\frac{(\begin{array}{c} 0 \\ 6 \\ 0 \end{array}) \cdot (\begin{array}{c} 2 \\ 1 \\ 4 \end{array})}{6 \cdot \sqrt{21}}$
	$=$	$\frac{6}{6 \cdot \sqrt{21}}$	$\cos^{- 1} ()$
$α$	$\approx$	$77 °$

Aufgabe 3B

Gleichschenkliges Dreieck

Geradengleichung aufstellen

Hast du eine Frage oder Feedback?

Punkt M

Vektoren berechnen

Winkel berechnen

Hast du eine Frage oder Feedback?

Geraden aufstellen

Punkte aufstellen

Hast du eine Frage oder Feedback?

Nachweis des Rechtecks

Hast du eine Frage oder Feedback?

Punkt $M$