Teil 2
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Aufgaben und Lösungen der Mathe Realschulprüfung 2021 vom Hauptteil 2.
Taschenrechner und Formelsammlung sind in diesem Prüfungsteil erlaubt.
Aufgaben des Teil 2 der Realschulprüfung 2021. Zum Download hier.
- 1
- 2
Die Abbildung zeigt einen Würfel mit der Kantenlänge .
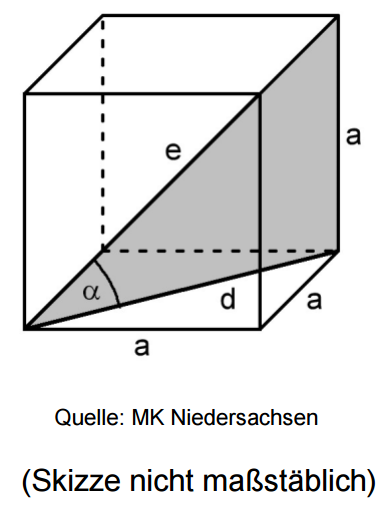
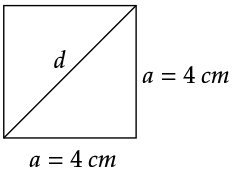
Berechne die Länge der Flächendiagonalen d in der Grundfläche des
Würfels. (2 BE)
Berechne die Größe des Winkels α. (3 BE)
(Solltest du Teilaufgabe a) nicht gelöst haben, rechne mit weiter.)
Zeige mithilfe einer Rechnung, dass die Länge der Raumdiagonalen e mit der Formel berechnet werden kann. (2 BE)
- 3
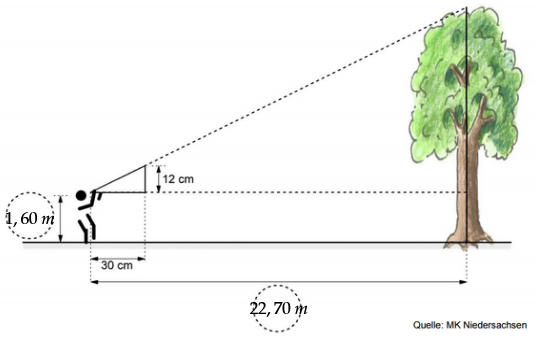
Erik bestimmt mit einem Peildreieck die Höhe eines Baumes. Er steht 22,70 m vom Baum entfernt und hält die Unterkante des Peildreiecks in einer Höhe von 1,60 m.
Übertrage die fehlenden Größen in die Skizze. (1 BE)
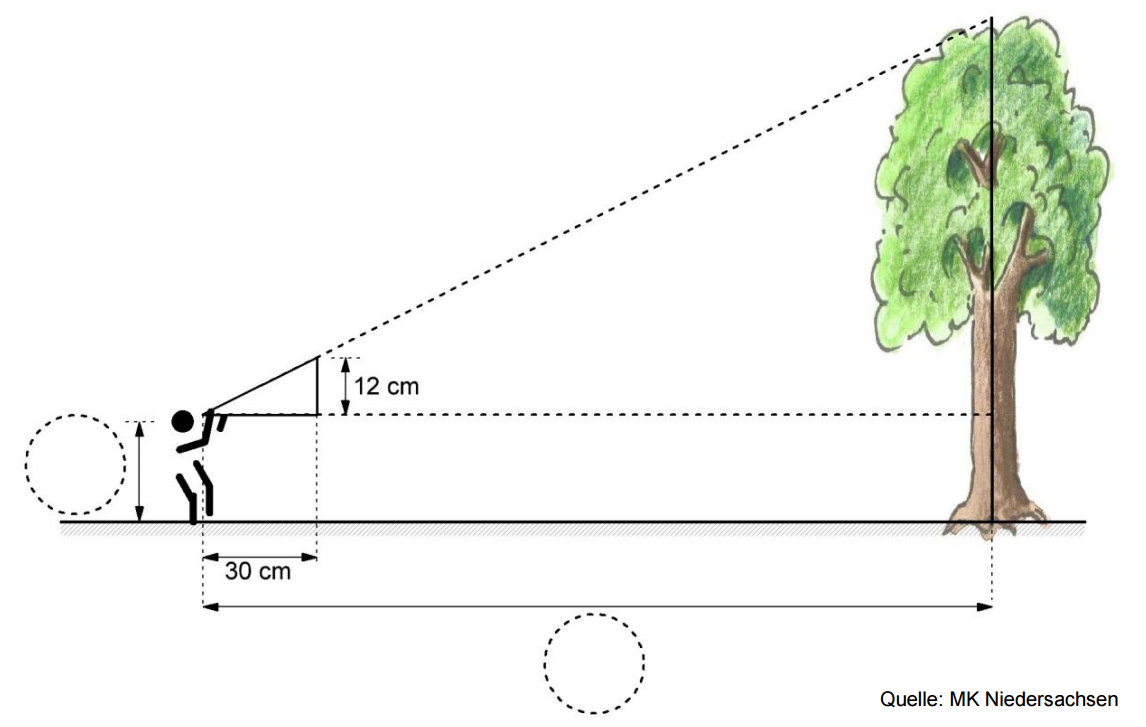
(Skizze nicht maßstäblich)
Berechne die Höhe des Baumes. (3 BE)
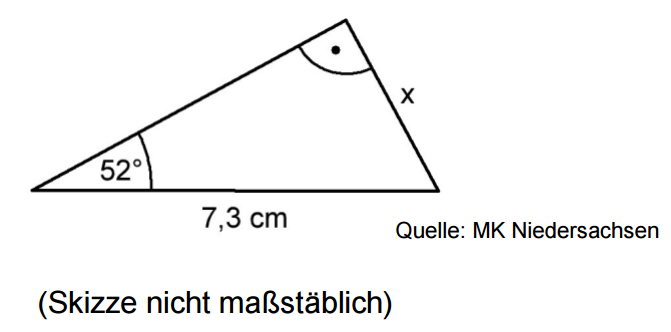
Leonie will ein zweites Dreieck zeichnen.
Es soll zum abgebildeten Dreieck ähnlich sein.
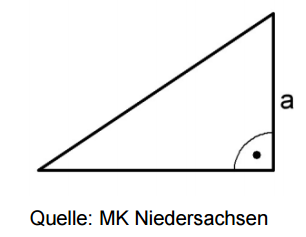
Ergänze Leonies Satz. (1 BE)
„Wenn ich die Seite a verdopple, dann muss ich
,
damit die Dreiecke ähnlich sind."
- 4
Mustafa möchte eine Kugelbahn bauen. Er hat
den abgebildeten Baustein hergestellt.
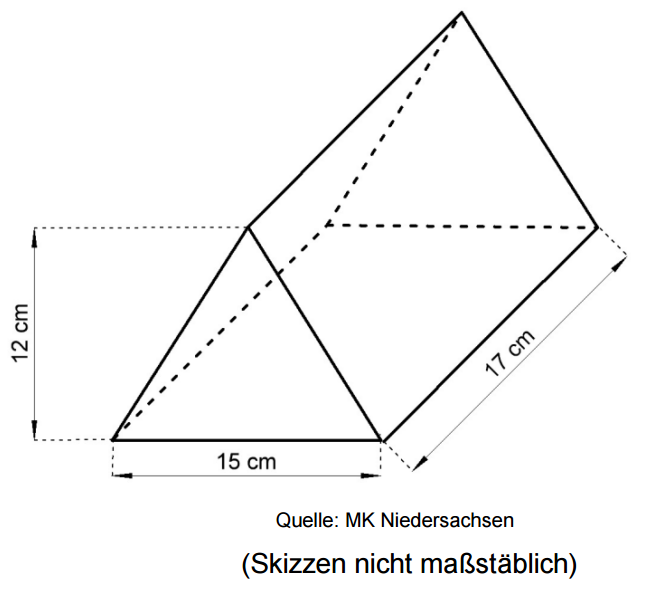
Nenne den Fachbegriff für den geometrischen Körper. (1 BE)
Berechne das Volumen des Bausteins. (2 BE)
Aus dem Baustein höhlt Mustafa einen Tunnel für die Kugelbahn aus.
Mustafa bemalt die Vorderseite des Bausteins dunkelgrau. (3 BE)
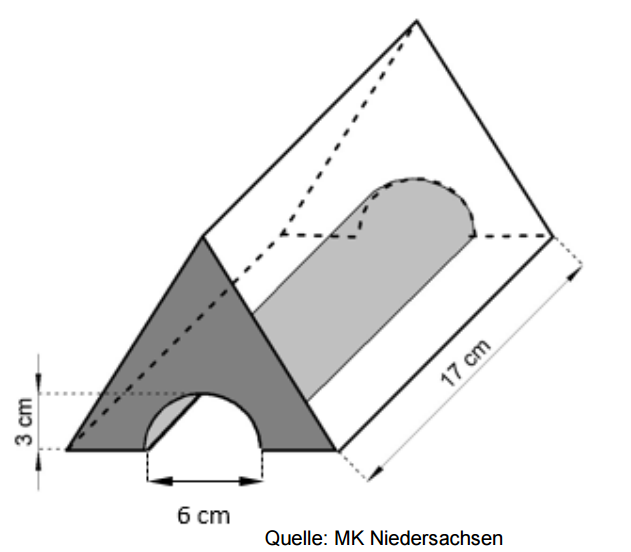
Berechne den Flächeninhalt der vorderen Fläche des Bausteins.
Mustafa streicht die Wand des Tunnels.
Berechne den Flächeninhalt der zu streichenden Fläche. (2 BE)
Eine Kugel mit V = 15,59 cm³ soll durch den Tunnel gerollt werden.
Überprüfe, ob die Kugel durch den Tunnel passt. (3 BE)
- 5
In dem Koordinatensystem ist der Graph der linearen Funktion abgebildet.
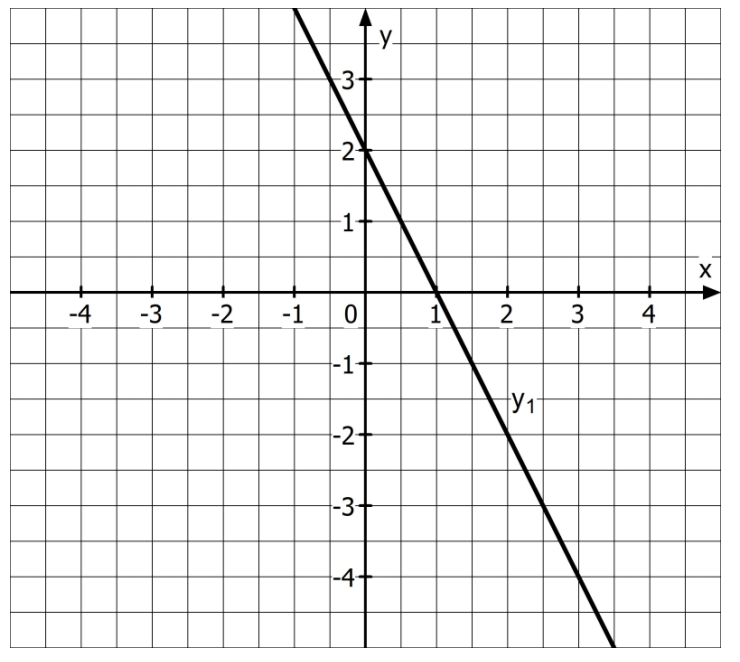
Quelle: MK Niedersachsen
Kreuze die passende Funktionsgleichung an. (1 BE)
Eine weitere lineare Funktion mit der Gleichung ist gegeben.
Gib die Koordinaten des Schnittpunktes der Funktionen und an. (3 BE)
Überprüfe mithilfe einer Rechnung, ob der Punkt P(–8|–7) auf dem Graphen der Funktion liegt. (3 BE)
- 6
- 7
In der Lösungsformel für quadratische Gleichungen fehlt eine Zahl für die Variable .
Gib eine Zahl für an, sodass die Lösungsformel genau ein Ergebnis hat. (1 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?