Wahlteil

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

Aufgaben des Teil 2 mit Wahlteil (ab S. 6) der Realschulprüfung 2021. Zum Download hier.

1
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
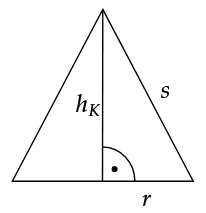
Ein Kegel wird halbiert.
Der halbe Kegel hat den Radius $r=6\ cm$ und die Höhe $h_k=12\ cm$ .
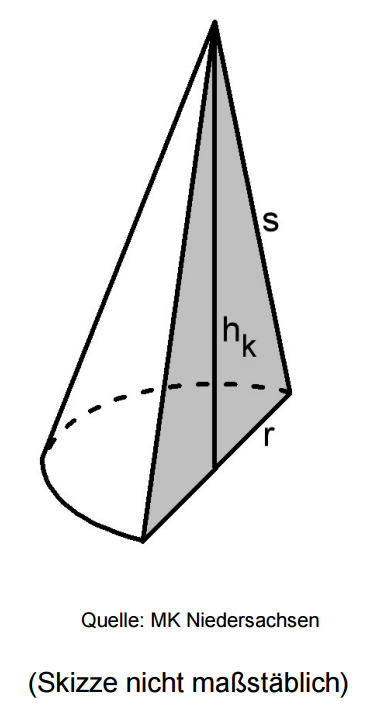
1. Berechne die Länge der Mantellinie s. (2 BE)
2. Berechne die Oberfläche des abgebildeten Körpers (halber Kegel). (4 BE)
  (Solltest du Teilaufgabe a) nicht gelöst haben, rechne mit $s=13{,}21cm$ weiter.)
3. Berechne das Volumen des halben Kegels. (2 BE)
4. Stelle für einen anderen halben Kegel mit $h_k=2r$ eine allgemeine Volumenformel in Abhängigkeit von $r$ auf und fasse sie so weit wie möglich zusammen. (2 BE)
2
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Lea steht an der Grundlinie eines Volleyballfeldes und schlägt den Ball auf.
Der Graph im Diagramm beschreibt annähernd die parabelförmige Flugbahn dieses Volleyballs. Er hat die Funktionsgleichung $y=-0{,}02(x-6)^2+2{,}5$ .
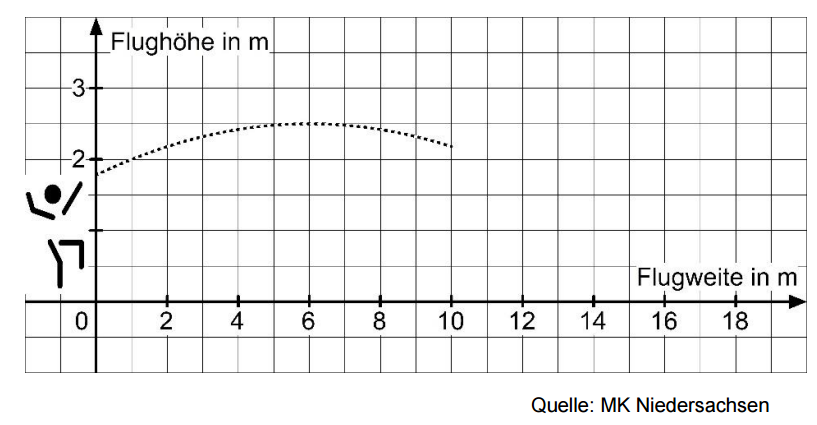
1. Ergänze den folgenden Satz. (2 BE)
2. Der Schnittpunkt mit der y-Achse ist die Aufschlaghöhe des Balles.
  Berechne die Aufschlaghöhe des Balles. (2 BE)
3. In der Mitte des 18 m langen Spielfeldes steht das Volleyballnetz. Es ist 2,04 m hoch.
  Fliegt der Ball über das Netz? Begründe deine Antwort mithilfe einer Rechnung. (3 BE)
4. Entscheide mithilfe einer Rechnung, ob der Ball im Spielfeld landet. (3 BE)
3
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
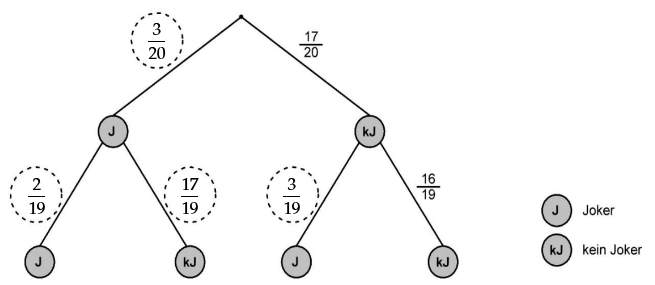
Lars spielt mit einem Kartenspiel aus 20 Karten. In dem Kartenspiel sind drei Karten „Joker“. Lars zieht nacheinander zwei Karten.
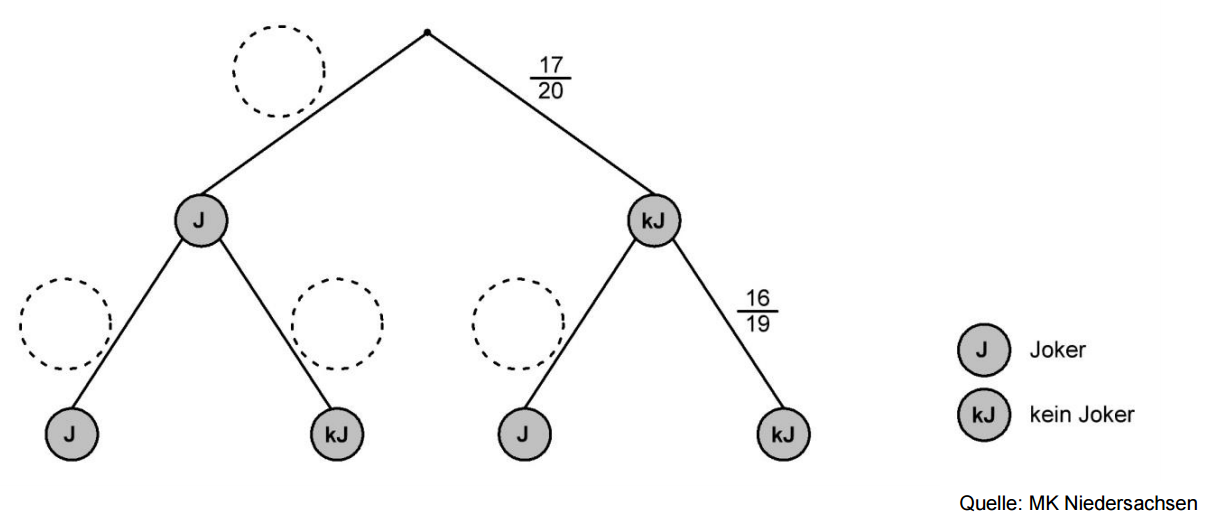
1. Entscheide anhand des Baumdiagramms, ob Lars die erste gezogene Karte in das Kartenspiel zurückgelegt hat oder nicht. Begründe deine Entscheidung. (2 BE)
2. Berechne die Wahrscheinlichkeit, dass Lars zweimal hintereinander keinen Joker zieht. (2 BE)
3. Ergänze im Baumdiagramm die fehlenden Wahrscheinlichkeiten. (2 BE)
4. Lars gewinnt, wenn er bei zweimaligem Ziehen mindestens einen Joker bekommt.
  Berechne die Wahrscheinlichkeit dafür, dass er gewinnt. Gib die Wahrscheinlichkeit in Prozent an. (2 BE)
5. Nora zieht Karten aus demselben Kartenspiel. Sie berechnet eine Wahrscheinlichkeit für ein Ereignis mit $P=1-\frac{17}{20}\cdot\frac{16}{19}$ .
  Beschreibe ein passendes Ereignis zu Noras Rechnung. (2 BE)
4
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Der schiefe Turm von Pisa ist geneigt. Der Winkel $𝛼$ beträgt $4°$ .
Die Aussichtsplattform im 7. Stockwerk hat an der geneigten Seite eine Höhe von $h=47{,}27\ m$ über dem Boden.
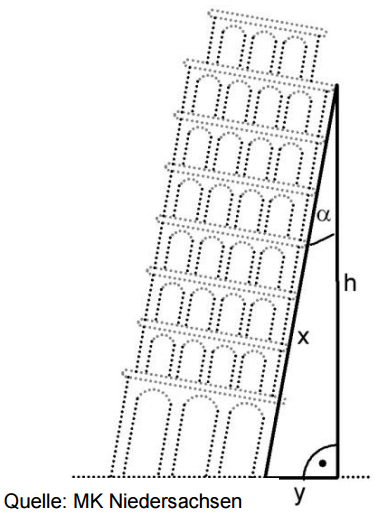
1. Berechne die Entfernung x vom Fußpunkt des Turmes bis zur Aussichtsplattform.
  (3 BE)
2. Berechne den Überhang $y$ des Turmes. (2 BE)
3. Quelle
  Der schiefe Turm von Suurhusen in Ostfriesland hat bei einer Höhe von 23,37 m über dem Boden einen
  Überhang von 2,47 m.
  Entscheide mithilfe einer Rechnung, welcher der beiden Türme im Guinness-Buch der Rekorde als schiefster Turm stehen müsste. (3 BE)
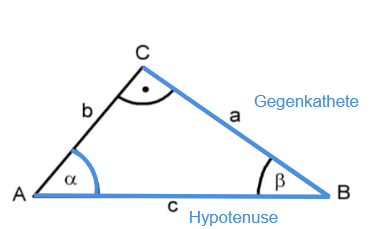
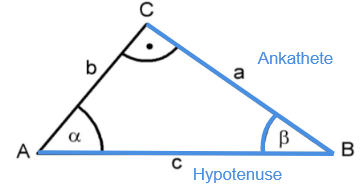
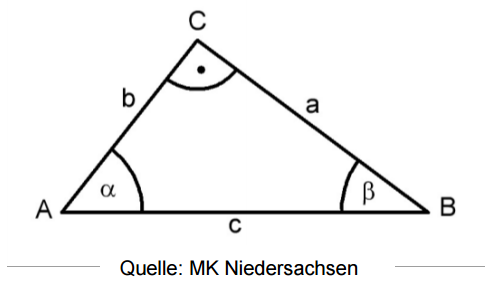
4. Zeige mithilfe der Abbildung, dass in jedem rechtwinkligen Dreieck ABC mit $γ=90°$ gilt:
  (2 BE)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?