Wahlteil 1 - WTR

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

Aufgaben zu Prüfung IGS E 2021, Wahlteil 1 - WTR. Zum Download hier.

Aufgabe 5

Ein Kernkraftwerk wurde dauerhaft abgeschaltet. Seitdem wartet man darauf, dass die Radioaktivität so gering wird, dass das Kernkraftwerk abgebaut werden kann.

Radioaktivität wird in der Einheit Terabecquerel (TBq) angegeben.

Im Jahr $2013$ wurde die Radioaktivität gemessen. Der Wert steht in folgender Tabelle:

Gehe davon aus, dass die Radioaktivität jährlich um $2{,}3 \%$ abnimmt.

Fülle die Tabelle aus. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentrechnung mittels Formeln
Erstes Jahr
Die Dezimalschreibweise für $2{,}3\%$ ist $2{,}3:100=0{,}023$ .
Also nimmt die Radioaktivität zwischen 2013 und 2014 um $0{,}023\cdot 1600=36{,}8$ ab. Damit bleibt 2014 noch $1600-36{,}8=1563{,}2$ übrig.
Zweites Jahr
Im zweiten Jahr nimmt die Radioaktivität um $0.023\cdot {\color{blue}1563{,}2}=35.9536$ ab. Also bleibt 2015 noch $1563{,}2-35{,}956\approx1527{,}25$ übrig.
Damit ist die fertige Tabelle:
Jahr
2013
2014
2015
Radioaktivität in $TBq$
$1600$
$1563{,}2$
$1527{,}25$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne wie viel Radioaktivität zwischen 2013 und 2014 verschwindet
Berechne wie viel Radioaktivität übrig bleibt
Wiederhole diese Schritte für das Jahr 2015
Stelle eine Funktionsgleichung der Form $f(x)=c \cdot a^{x}$ auf, die die Abnahme der Radioaktivität ab dem Jahr $2013$ beschreibt.
Erkläre die Bedeutung von $c, a, x$ und $f(x)$ im Sachzusammenhang. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
Bedeutung im Sachzusammenhang
Die Variable $x$ ist die Anzahl der Jahre seit 2013
Die Funktion $f(x)$ ist die Radioaktivität in $TBq$ im Jahr $2013+x$
Der Startwert $c$ ist die Radioaktivität im Jahr 2013 in $TBq$
Der Zerfallsfaktor $a$ ist der Faktor um den $f(x)$ pro Jahr fällt
Den Startwert bestimmen
Der Startwert $c$ ist die Radioaktivität im Jahr $2013$ . Nach der Tabelle aus der a) ist er also:
Den Zerfallsfaktor bestimmen
Pro Jahr sinkt die Radioaktivität mit einem Faktor von $0{,}023$ . Also ist der Zerfallsfaktor:
Damit ist die fertige Funktion:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Überlege dir die Bedeutungen im Sachzusammenhang
Bestimme $c$ mit der Tabelle aus der a)
Berechne $a$ mit der prozentualen Änderung aus der a)
Berechne, wie hoch die Radioaktivität nach diesem Modell im Jahr 2021 ist. (2 BE)
(Wenn du b) nicht gelöst hast, verwende $f(x)=1595 \cdot 0{,}976^{x}$ .)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
Anzahl der Jahre berechnen
Zwischen 2013 und 2021 liegen $2021-2013=8$ Jahre.
Funktion anwenden
Wie suchen die Radioaktivität $8$ Jahre nach 2013. Also ist $x=8$ und wir rechnen:
Also ist 2021 noch $1328{,}23\;TBq$ übrig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Anzahl der Jahre seit 2013
Berechne die Radioaktivität mit der Formel aus der b)
Das Kernkraftwerk wurde 1980 abgeschaltet.
Berechne, wie hoch die Radioaktivität nach diesem Modell im Jahr 1980 war. (2 BE)
Anzahl der Jahre
Zwischen 2013 und 1980 liegen $1980-2013=-33$ Jahre.
Anwenden der Funktion
Wir suchen die Radioaktivität vor $33$ Jahren. Also ist $x=-33$ und wir rechnen:
Damit lag die Radioaktivität $1980$ noch bei $3448{,}26\;TBq$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Anzahl der Jahre seit 2013
Berechne die Radioaktivität mit der Formel aus der b)

Jahr	2013	2014	2015
Radioaktivität in $TBq$	$1600$	$1563{,}2$	$1527{,}25$

Bestimme, wann die Radioaktivität nach diesem Modell auf die Hälfte des Werts von 2013 gesunken ist. (3 BE)

Wenn die Radioaktivität bei $0{,}000 00001 \mathrm{TBq}$ liegt, kann das Kraftwerk ohne Schutzkleidung abgebaut werden.
Gerald meint: „Dann könnte das Kraftwerk ja erst im Jahr 3121 abgebaut werden!“
Überprüfe Geralds Aussage. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
Radioaktivität berechnen
Zwischen 2013 und 3121 liegen $3121-2013=1108$ Jahre. Also ist $x=1108$ und wir rechnen:
Mit dem Taschenrechner kriegt man dann: $f(1108)\approx 1{,}01\cdot 10^{-8}$
Sicherheit überprüfen
Es gilt $1{,}01\cdot 10^{-8}\approx0{,}00000001$ . Also kann das Kraftwerk im Jahr 3121 sicher abgebaut werden und Geralds Aussage stimmt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Radioaktivität im Jahr 3121
Überprüfe ob dann das Kraftwerk sicher abgebaut werden kann
Exponentielle Prozesse können für kurze Zeiträume auch linear modelliert werden, um Berechnungen zu vereinfachen.
Im Jahr 2013 betrug die Radioaktivität $1600$ TBq. Drei Jahre später betrug sie $1492{,}1$ TBq.
Bestimme die Gleichung für eine lineare Funktion auf Grundlage dieser Werte. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
$y$ -Achsenabschnitt
Bei $x=0$ soll die lineare Funktion die Radioaktivität im Jahr 2013 annehmen. Also ist der $y$ -Achsenabschnitt:
Steigung
Um die Steigung zu berechnen nutzen wir das Steigungsdreieck. Dazu brauchen wir erst die Differenzen. Wir rechnen:
Also ist die Steigung:
Damit ist die fertige Funktion:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme den $y$ -Achsenabschnitt der Geraden
Berechne die Steigung mit dem Steigungsdreieck
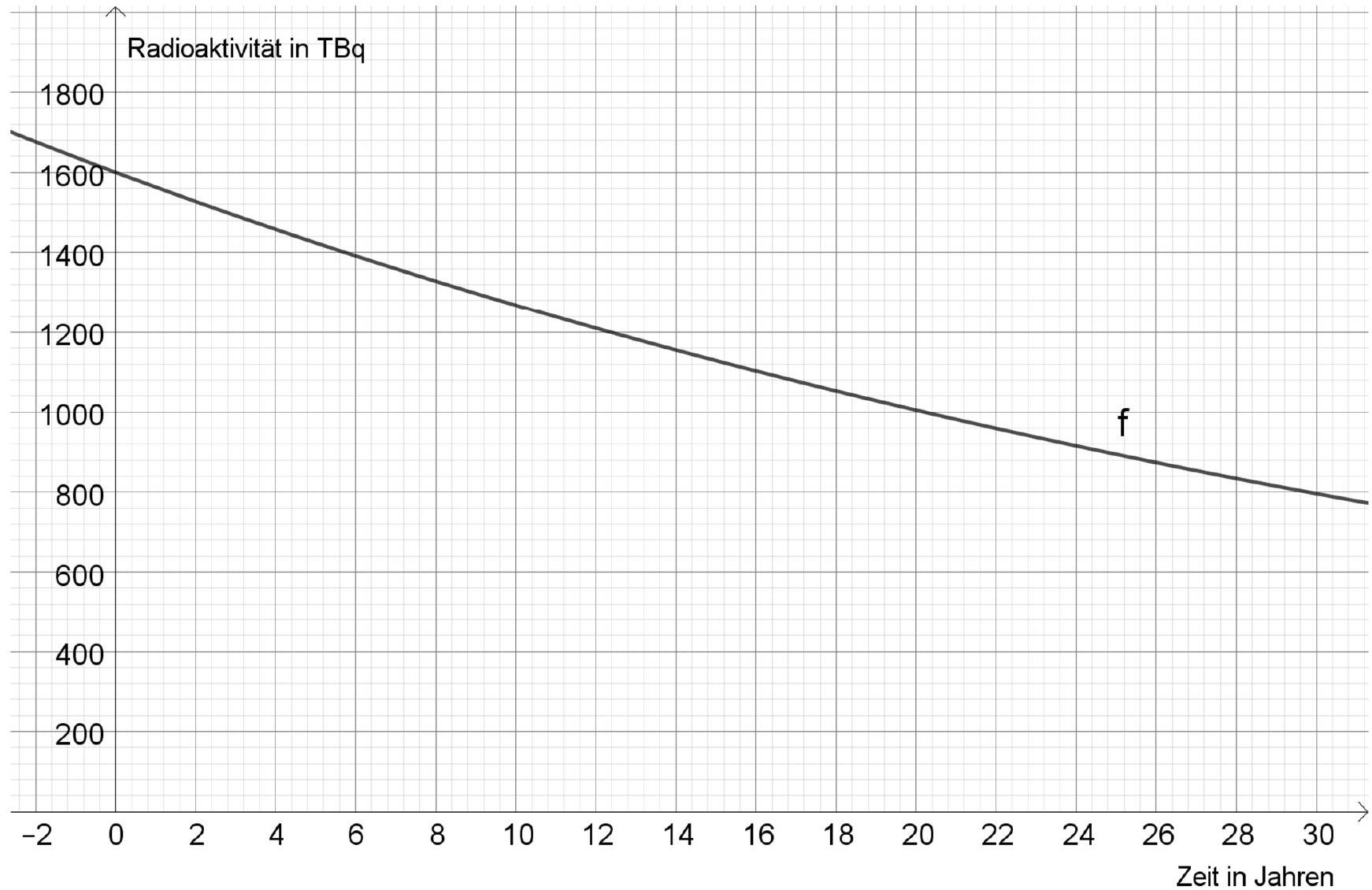
Im Koordinatensystem ist bereits die Exponentialfunktion aus b) eingezeichnet.
Zeichne die lineare Funktion in das Koordinatensystem ein.
Bestimme mithilfe der Zeichnung, nach wie vielen Jahren die Abweichung zur Exponentialfunktion erstmals größer als $200$ TBq ist. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Graph einzeichnen
Wir tragen zuerst den $y$ -Achsenabschnitt ein. Danach setzen wir das Steigungsdreieck aus der g) an und ziehen eine Linie durch die beiden Punkte.
Abweichung bestimmen
Mit einem Geodreieck sehen wir, dass bei $x=26$ die Differenz der Graphen etwa $200\;TBq$ beträgt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zeichne den $y$ -Achsenabschnitt und ein Steigungsdreieck ein
Zeichne die Gerade ein
Finde den $x$ -Wert, bei dem die beiden Graphen eine Entfernung von $200$ haben

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle 800$	$=$	$\displaystyle 1600\cdot 0.977^x$	$\displaystyle :1600$
	↓	Den Faktor nach links bringen
$\displaystyle \frac{800}{1600}$	$=$	$\displaystyle 0.977^x$
	↓	Kürzen
$\displaystyle \frac{1}{2}$	$=$	$\displaystyle 0.977^x$	$\displaystyle \log_{0{,}977}$
	↓	Logarithmus anwenden
$\displaystyle \log_{0{,}977}\left(\frac{1}{2}\right)$	$=$	$\displaystyle x$
	↓	Mit dem Taschenrechner ausrechnen
$\displaystyle 29{,}79$	$≈$	$\displaystyle x$

Wahlteil 1 - WTR

Aufgabe 5

Erstes Jahr

Zweites Jahr

Hast du eine Frage oder Feedback?

Bedeutung im Sachzusammenhang

Den Startwert bestimmen

Den Zerfallsfaktor bestimmen

Hast du eine Frage oder Feedback?

Anzahl der Jahre berechnen

Funktion anwenden

Hast du eine Frage oder Feedback?

Anzahl der Jahre

Anwenden der Funktion

Hast du eine Frage oder Feedback?

Berechnen der Halbwertszeit

Hast du eine Frage oder Feedback?

Radioaktivität berechnen

Sicherheit überprüfen

Hast du eine Frage oder Feedback?

yyy-Achsenabschnitt

Steigung

Hast du eine Frage oder Feedback?

Graph einzeichnen

Abweichung bestimmen

Hast du eine Frage oder Feedback?

$y$ -Achsenabschnitt