Wahlteil 1 - GTR
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Aufgaben zu Prüfung IGS G 2021, Wahlteil 1 - GTR. Zum Download hier.
- 1
Aufgabe 5
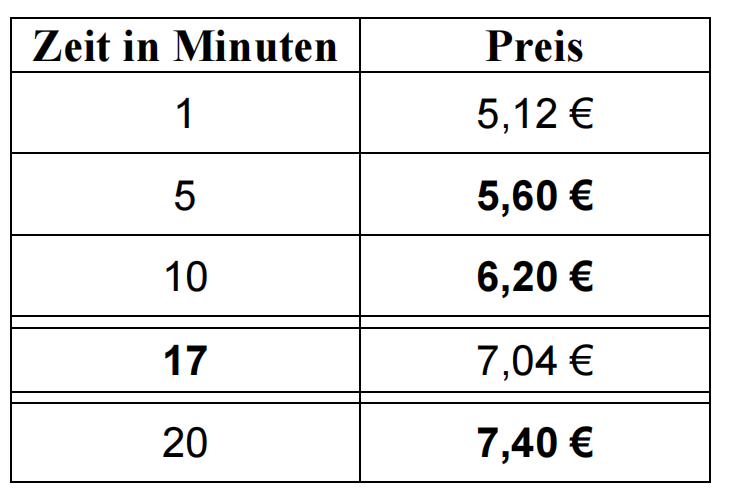
Anja mietet einen E-Roller der Firma FLIP.
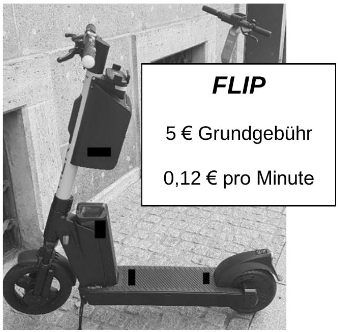
Berechne, was eine Rollerfahrt von 3 Minuten kostet. (2 BE)
Erkläre, warum in der Tabelle in (c) für 1 Minute ein Preis von 5,12 € steht. (1 BE)
Vervollständige die Tabelle. (3 BE)
Stelle eine Funktionsgleichung auf, mit der der Preis berechnet werden kann. (2 BE)
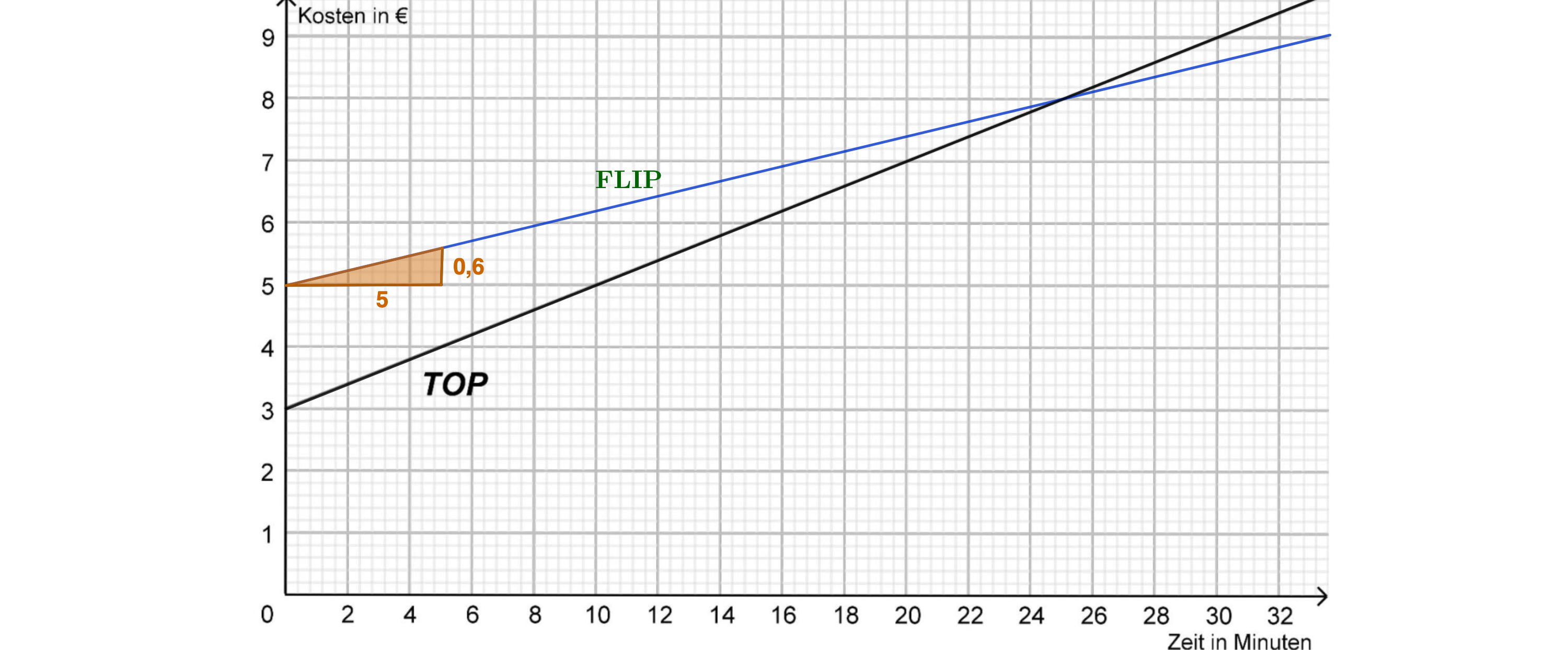
Zeichne den Graphen zum Angebot der Firma FLIP in das Koordinatensystem. (2 BE)
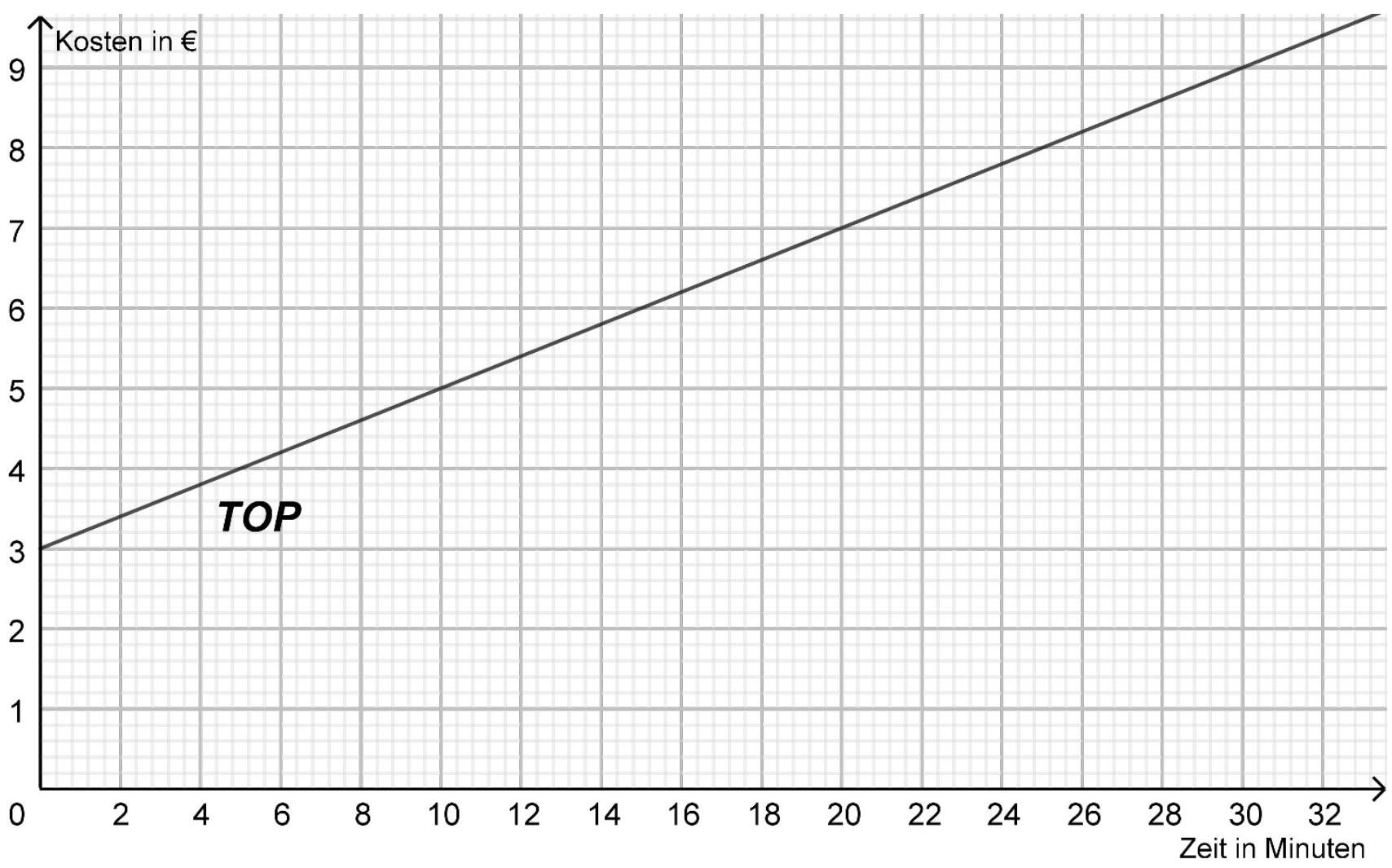
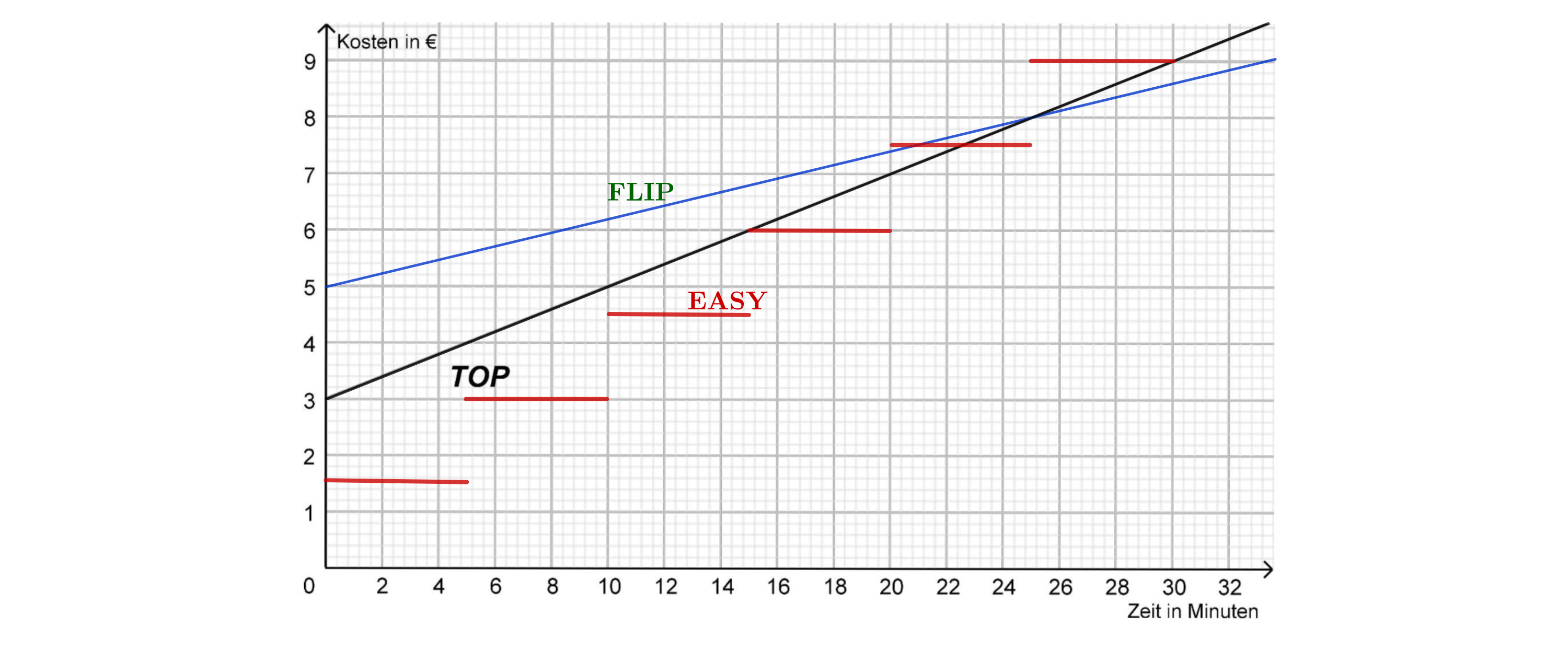
Im Koordinatensystem ist bereits der Graph für ein Angebot der Firma TOP zu sehen.
Fülle mithilfe des Graphen die folgende Information aus. (2 BE)
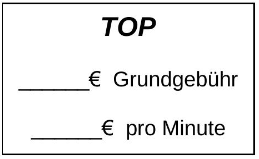
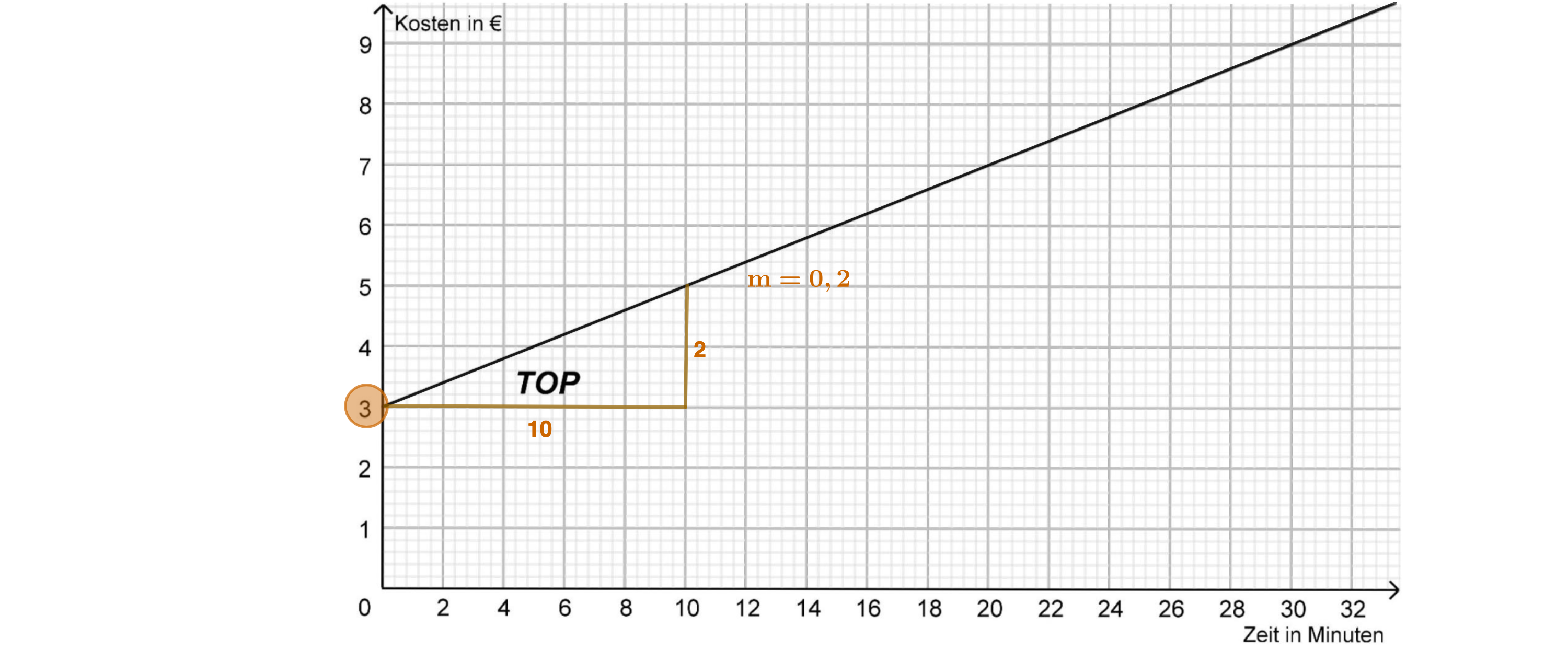
Anja hat für das Angebot der Firma TOP eine Funktionsgleichung aufgestellt:
Bestimme mithilfe des GTR den Schnittpunkt der beiden Funktionsgraphen.
Dokumentiere dein Vorgehen. (3 BE)
Erkläre die Bedeutung des Schnittpunkts im Sachzusammenhang.
(Wenn du d) nicht gelöst hast, verwende .)
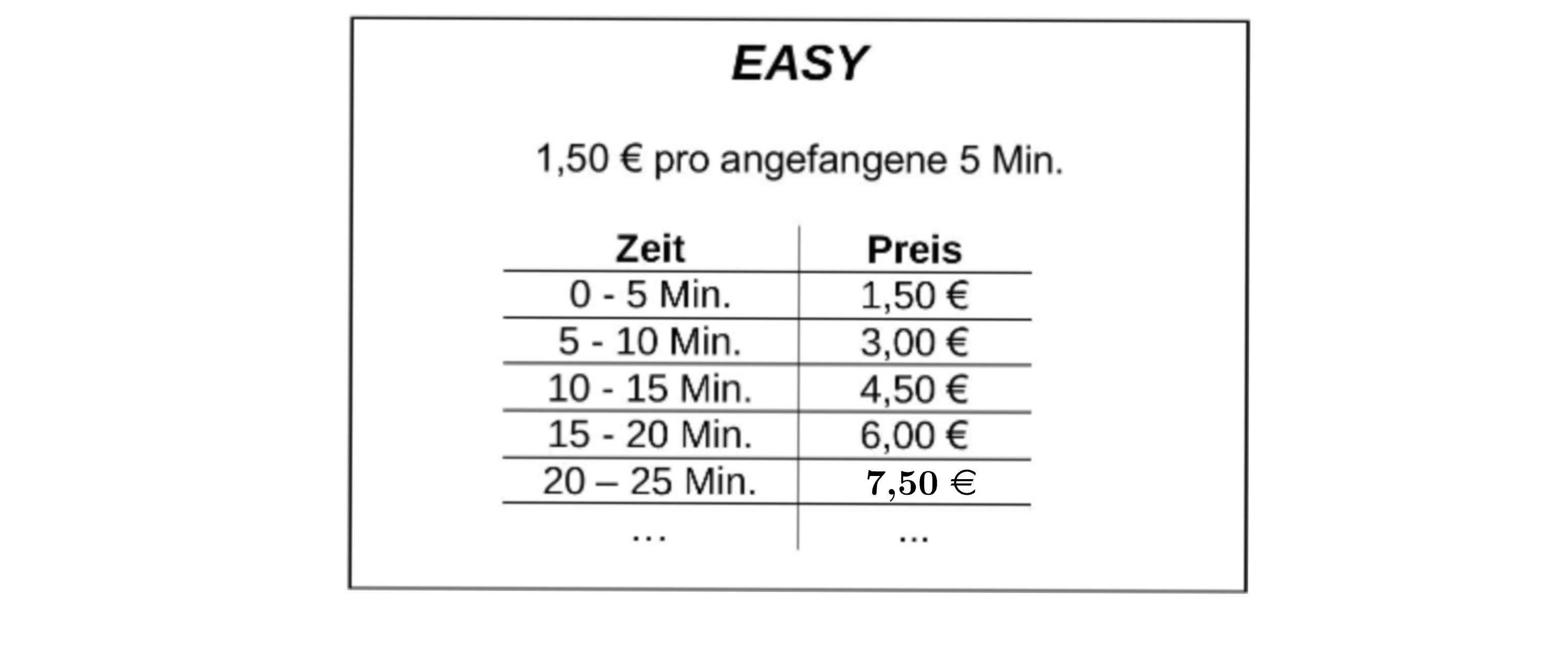
Die Firma EASY macht das nachfolgende Angebot.
Beschreibe, wie sich dieses Angebot von den anderen beiden Angeboten unterscheidet.
Ergänze in der Tabelle den fehlenden Preis. (2 BE)
Easy
1,50 € pro angefangene 5 Min.
Zeichne das Angebot der Firma EASY in das Koordinatensystem ein. (1 BE)
Anja überlegt, einen E-Roller der Firma EASY für die Fahrt zur Schule zu mieten.
Ihre Schule ist von zu Hause entfernt.
Mit dem Roller fährt sie durchschnittlich pro Stunde.
Bestimme die Kosten. (2 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?