Prüfungsteil 2 2022
🎓 Prüfungsbereich für Nordrhein-Westfalen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Aufgaben aus dem Prüfungsteil 2 der ZP 10 Mathe 2022 für den MSA mit ausführlichen Musterlösungen.
Für diese Aufgaben stehen dir in der Zentralen Prüfung 90 Minuten Bearbeitungszeit zur Verfügung. Taschenrechner und Formelsammlung sind für diesen Prüfungsteil erlaubt.
- 1
Aufgabe 1: Rösti
Ein Unternehmen stellt nach eigenem Rezept aus Kartoffeln sogenannte Rösti her (Abbildung 1 und 2). Dazu wird der Teig in eine zylindrische Form gegossen (Abbildung 3) und anschließend gebacken. Für ein Rösti benötigt man Teig.

Abbildung 1: Rösti aus Kartoffeln
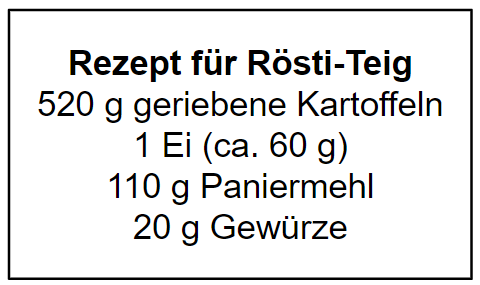
Abbildung 2: Rezept für Rösti-Teig

Abbildung 3: zylindrische Form
Zeige rechnerisch, dass aus der Teigmenge eines Rezeptes sieben Rösti hergestellt werden können (Abbildung 2). (2 P)
Teig haben ein Volumen von .
Berechne, wie viel Gramm ein Kubikzentimeter Teig wiegt. (2 P)
Ein Rösti soll dick sein und ein Volumen von haben.
Zeige, dass die zylindrische Form einen Durchmesser von ca. haben muss. (3 P)
Das Unternehmen möchte zusätzlich Mini-Rösti herstellen. Ein Mini-Rösti soll auch dick sein, aber nur das halbe Volumen haben. Ein Mitarbeiter behauptet: „Für ein Mini-Rösti brauchen wir eine Form mit halbem Durchmesser!“ Hat er recht?
Begründe deine Entscheidung. (3 P)
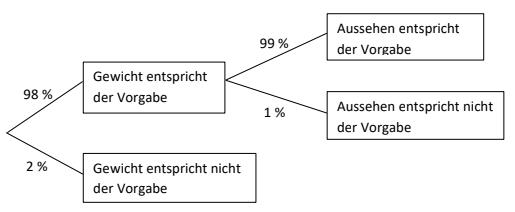
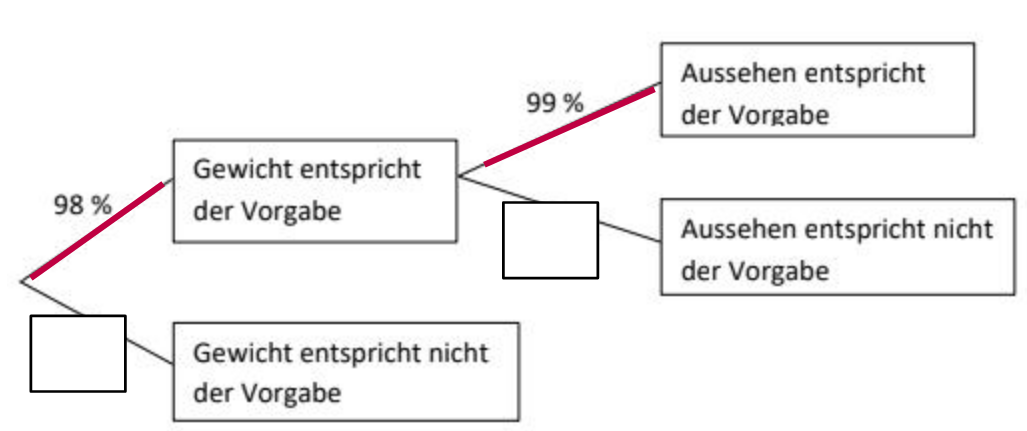
Bevor die Rösti verpackt werden, wird zuerst das Gewicht und dann das Aussehen kontrolliert. Alle Rösti, deren Gewicht oder deren Aussehen nicht der Vorgabe entsprechen, werden aussortiert. Das Baumdiagramm zeigt die Anteile. Die Anteile werden im Folgenden als Wahrscheinlichkeiten gedeutet.
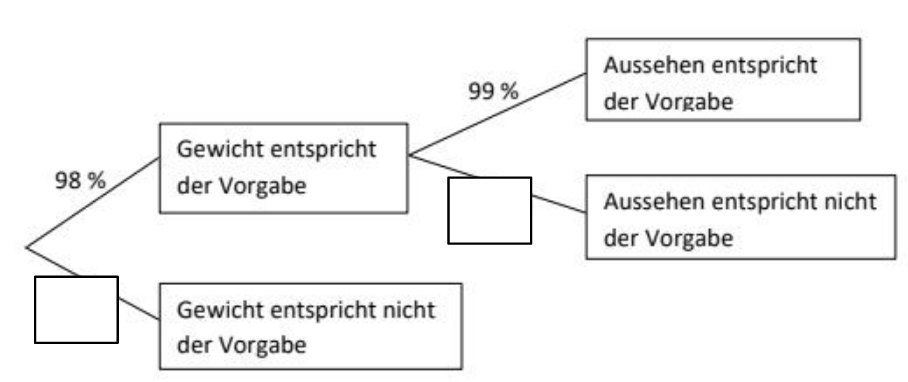
Ergänze die fehlenden Angaben im Baumdiagramm. (2 P)
Berechne, wie viel Prozent der Rösti insgesamt den Vorgaben entsprechen. (3 P)
Das Unternehmen kontrolliert an einem Tag 10000 Rösti.
Wie viele Rösti werden vermutlich aussortiert, weil sie nicht den Vorgaben entsprechen?
Notiere deine Rechnung. (3 P)
- 2
Aufgabe 2: Wassermelonen
Für ein Schulprojekt beschäftigt sich Sinja mit der Form und dem Wachstum von Wassermelonen.
Sinja hat eine nahezu kugelförmige Wassermelone gekauft, die einen Durchmesser von ca. hat (Abbildung 1).
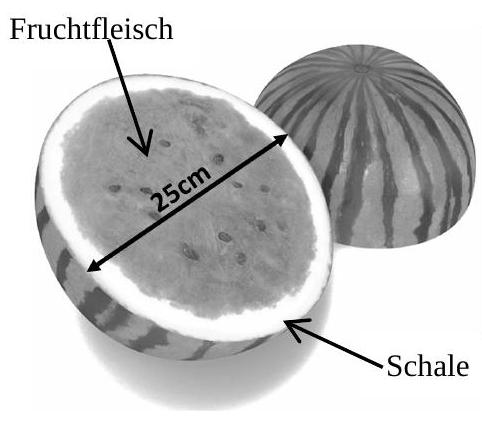
Abbildung 1: aufgeschnittene Wassermelone
Zeige rechnerisch, dass diese Wassermelone ein Volumen von hat. (3 P)
Die Schale der Wassermelone hat eine Dicke von (Abbildung 1).
Berechne den prozentualen Anteil des Fruchtfleisches an der ganzen Wassermelone. (3 P)
Sinja entdeckt würfelförmige Wassermelonen, die in Japan verkauft werden (Abbildungen 2).
Eine würfelförmige Wassermelone hat ebenfalls ein Volumen von .
Bestätige durch eine Rechnung, dass diese Wassermelone eine Kantenlänge von ca. hat. (2 P)

Abbildung 2: würfelförmige Wassermelone
Entscheide durch eine Rechnung, ob die kugelförmige oder die würfelförmige Wassermelone eine größere Oberfläche hat. (4 P)
Wassermelonen verdoppeln ihr Gewicht pro Woche unter idealen Wachstumsbedingungen. Sinja überlegt, wie sich das Gewicht einer schweren Wassermelone unter idealen Bedingungen voraussichtlich entwickelt. Sie erstellt dazu eine Tabelle. (2 P)

Berechne das Gewicht der Wassermelone nach 4 Wochen.
Sinja behauptet: „Der Graph in Abbildung 3 beschreibt das Wachstum dieser Wassermelone.“
Hat Sinja recht? Begründe deine Entscheidung. (3 P)
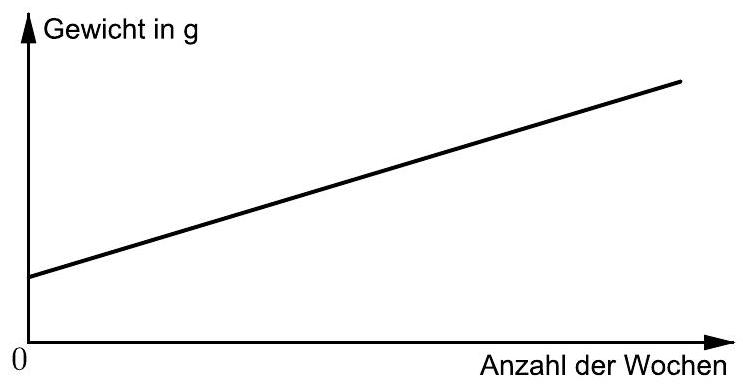
Abbildung 3: Graph zum Wachstum der Wassermelone
- 3
Aufgabe 3: Parabel und Rechteck
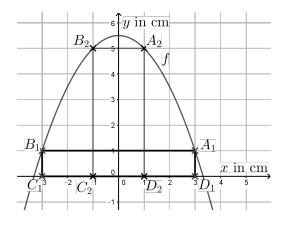
Julia zeichnet mithilfe einer Geometriesoftware die Parabel mit der Funktionsgleichung in ein Koordinatensystem (Abbildung 1).
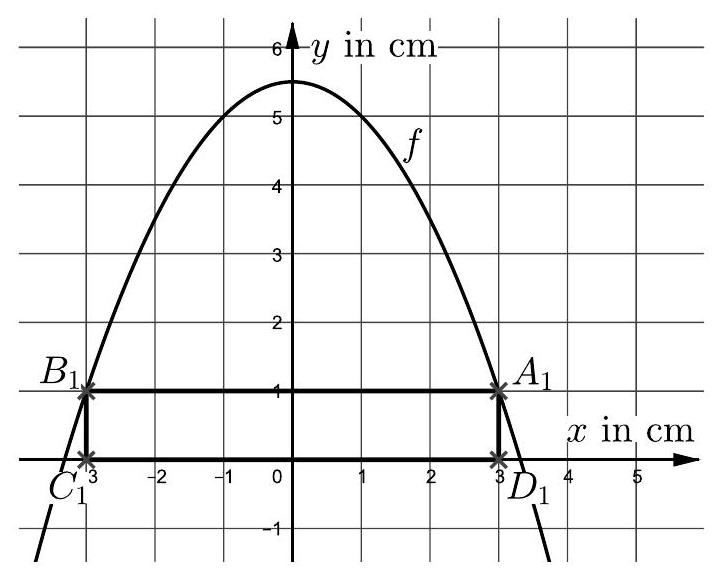
Abbildung 1: Parabel und Rechteck
Bestätige durch eine Rechnung, dass der Punkt auf der Parabel liegt. (2 P)
Begründe mit den Eigenschaften dieser Parabel, dass der Punkt ebenfalls auf dem Graphen von liegt. (3 P)
Die Punkte und liegen auf der -Achse und bilden mit den Punkten und das Rechteck .
Berechne den Umfang dieses Rechtecks. (2 P)
Ausgehend von anderen Punkten auf der Parabel kann man auf die gleiche Art weitere Rechtecke zeichnen.
(1) Zeichne den Punkt in Abbildung 1 ein. (1 P)
(2) Ergänze die drei weiteren Punkte und und verbinde die vier Punkte zu dem Rechteck . (2 P)
Mit dem Termkann man den Umfang für jedes dieser Rechtecke berechnen
Dabei ist und steht für die -Koordinate des zum Rechteck gehörenden Punktes usw.
Berechne mit dem Termden Umfang des Rechtecks, das durch den Punkt festgelegt ist. (2 P)
Julia vereinfacht den Termzu
Zeige durch Termumformungen, dass die beiden Termeundgleichwertig sind. (3 P)
Julia stellt die folgende Gleichung auf:
(1) Löse die Gleichung. (3 P)
(2) Erkläre das Ergebnis in Bezug auf die Rechtecke unter der Parabel . (1 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?