Heft 2 - B3
🎓 Prüfungsbereich für Schleswig-Holstein
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Aufgaben und Lösungen des Mathe MSA 2023 Prüfungsteil 2 Aufgabe 3.
Ein Taschenrechner ist in diesem Prüfungsteil erlaubt.
- 1
Die Phänomento-AG stellt Beispiele zusammen, wie man mit Mathematik und Naturwissenschaften alltägliche Dinge versteht. In diesem Halbjahr untersucht ein Team die Temperaturabnahme von Kaffee und Tee bei Raumtemperatur.
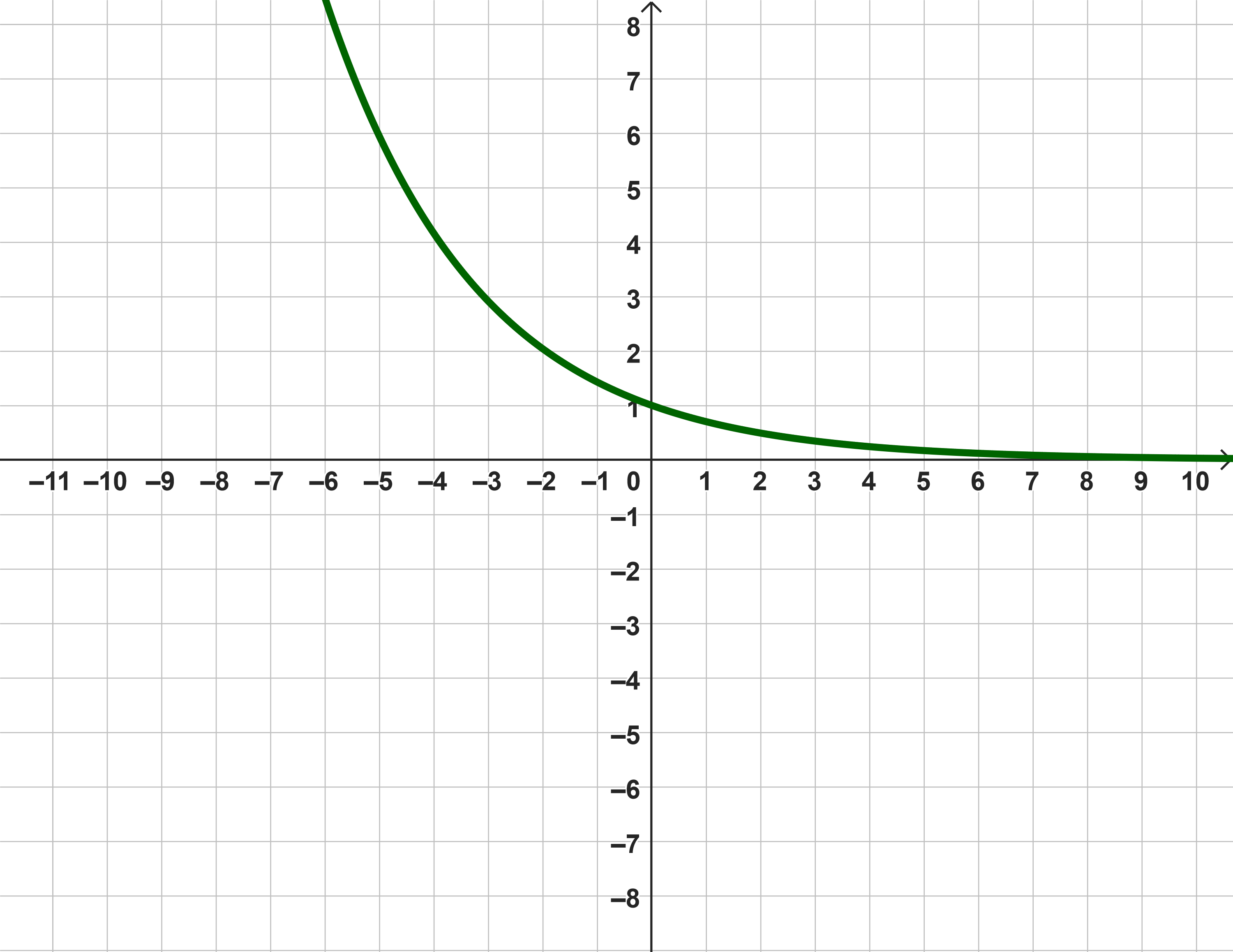
Ela und Ben beschreiben das Abkühlen von Tee mit folgender Funktionsgleichung, die der vergangenen Zeit in Minuten die Temperatur zuordnet:
Gib die Temperatur des Tees in nach 2 min an. (1 Punkt)
Bestimme, nach wie vielen Minuten der Tee die Raumtemperatur von erreichen müsste. (2 Punkte)
Sanni fragt: „Wie lange dauert es, bis der Tee auf abgekühlt ist?" Ari entgegnet: „Das kann doch hier gar nicht passieren."
Beurteile Aris Aussage. (1 Punkt)
Skizziere den Graphen, der den Zusammenhang nach der Modellierung dieser Gruppe darstellt. (1 Punkt)
- 2
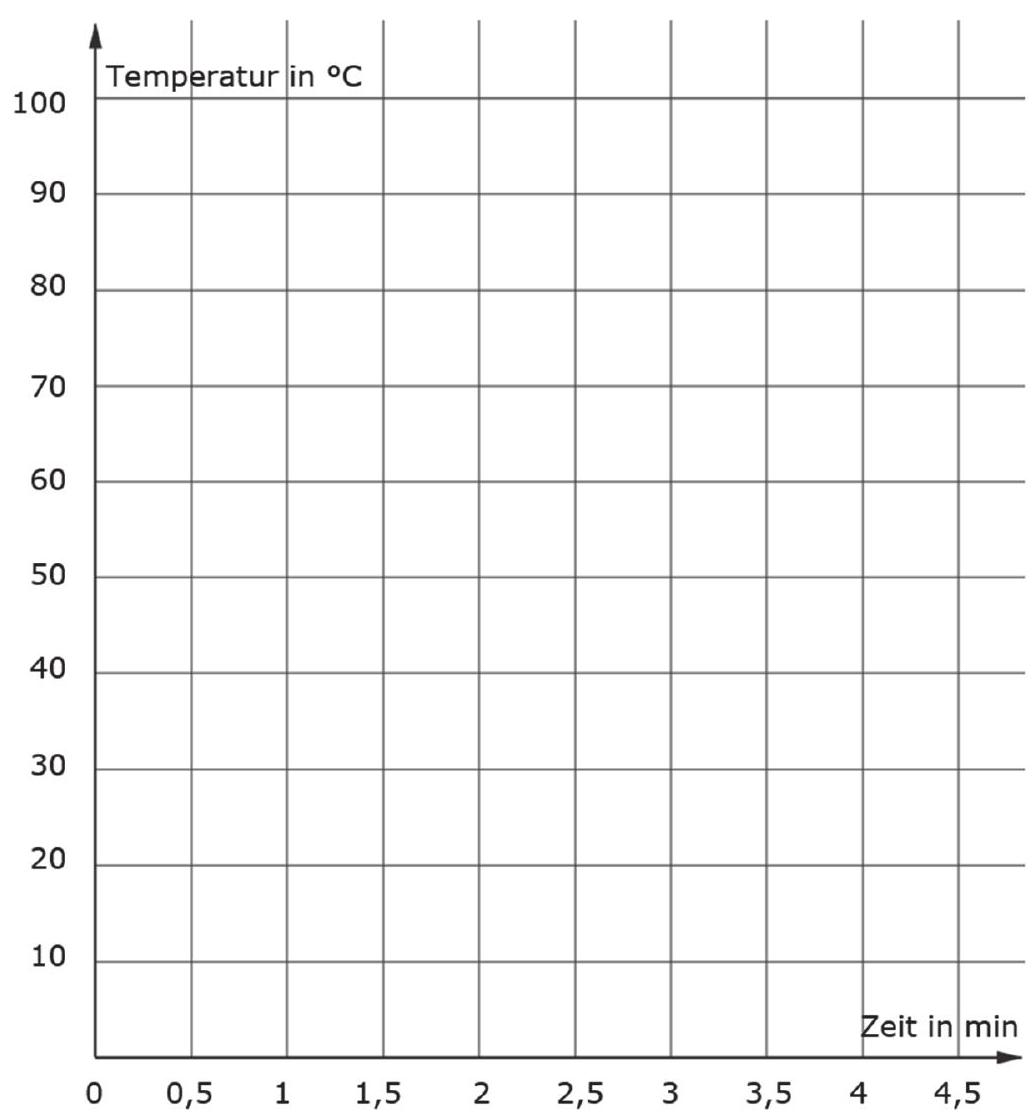
Eine andere Gruppe misst die Temperatur beim Abkühlen von Kaffee, der mit kochendem Wasser von aufgegossen wurde.
Die Tabelle zeigt die Temperatur zu verschiedenen Zeitpunkten.
vergangene Zeit in min
Temperatur in
0
100,0
1
89,0
2
79,2
3
70,5
Ben behauptet, dass der Zusammenhang weder linear noch antiproportional ist.
Begründe, dass Bens Behauptung korrekt ist. (2 Punkte)
Ela schlägt vor, die Abkühlung mit einer Exponentialfunktion zu beschreiben.
Gib eine Funktionsgleichung an, die den Prozess annähert. (2 Punkte)
- 3
Peter und Paula wollen untersuchen, welchen Einfluss die Anfangstemperatur auf die Dauer der Abkühlung von Getränken hat. Dazu beschreiben sie die Funktion mit der folgenden Gleichung:
Beschreibe, was die Parameter und im Kontext der Abkühlung von Getränken bedeuten. (2 Punkte)
Gib ein sinnvolles Intervall für an. (1 Punkt)
Paula fragt "Was ändert sich, wenn wir zum Funktionsterm noch ein addieren?" Die Funktionsgleichung sieht dann so aus:
Ordne die Funktionsgleichungen den passenden Graphen zu. (2 Punkte)
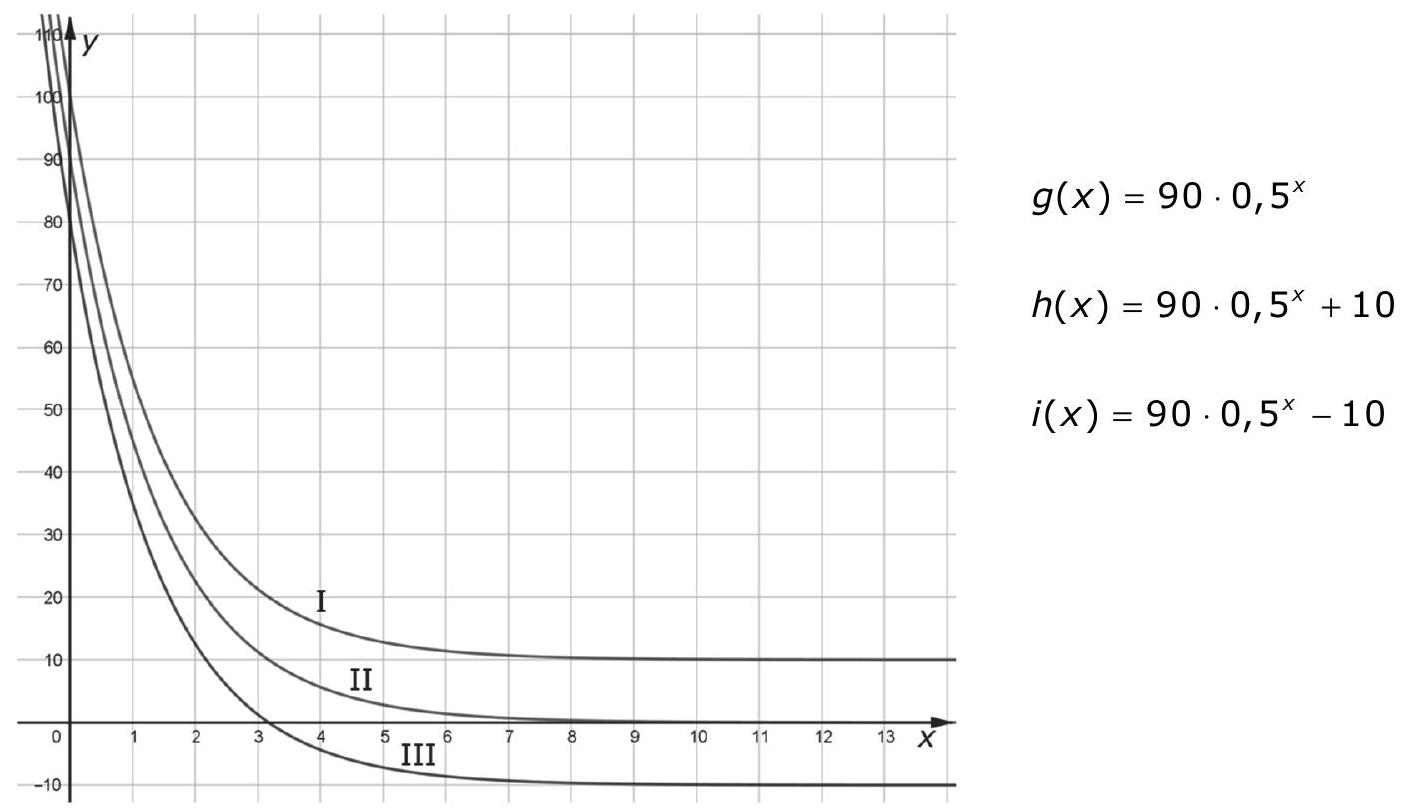
Beschreibe, wie sich die Veränderung des Parameters auf den Graphen auswirkt. (1 Punkt)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?