Geometrie, Teil A, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden.

Gleiche Aufgabe wie Geometrie, Teil A, Aufgabengruppe 1

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Mittelpunkte der Seitenflächen eines Würfels sind die Eckpunkte eines Oktaeders
(vgl. Abbildung).
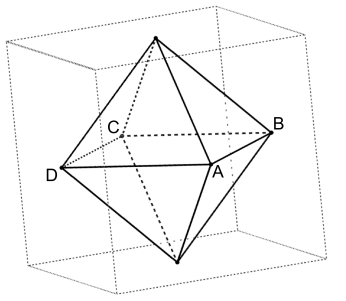
Die Eckpunkte $A (1 | 2 | 1), B, C (- 3 | - 6 | 9)$ und $D$ des Oktaeders liegen in der Ebene $H$ mit der
Gleichung $2 x_{1} + x_{2} + 2 x_{3} - 6 = 0$ .
1. Weisen Sie nach, dass die Kantenlänge des Würfels 12 beträgt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge eines Vektors
  Die Kantenlänge des Würfels soll 12 betragen
  Berechne den Betrag des Vektors $\vec{A C}$ .
  $\vec{A C} = \vec{O C} - \vec{O A} = (\begin{array}{c} - 3 \\ - 6 \\ 9 \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 1 \end{array}) = (\begin{array}{c} - 4 \\ - 8 \\ 8 \end{array})$
  $| \vec{A C} | = \sqrt{(- 4)^{2} + (- 8)^{2} + 8^{2}} = \sqrt{16 + 64 + 64} = \sqrt{144} = 12$
  Die Kantenlänge des Würfels beträgt $12 LE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Betrag des Vektors $\vec{A C}$ .
2. Bestimmen Sie die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in $H$ liegen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalenvektor – Umwandeln von Ebenendarstellungen
  Die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in H liegen.
  Die Spitze $S$ der oberen Pyramide liegt senkrecht über dem Mittelpunkt von $A C$ .
  $\vec{O M_{A C}} = \frac{1}{2} (\vec{O A} + \vec{O C}) = \frac{1}{2} (\begin{array}{c} 1 - 3 \\ 2 - 6 \\ 1 + 9 \end{array}) = \frac{1}{2} (\begin{array}{c} - 2 \\ - 4 \\ 10 \end{array}) = (\begin{array}{c} - 1 \\ - 2 \\ 5 \end{array})$
  Weiterhin kann der Normalenvektor der Ebene $H$ abgelesen werden:
  ${\vec{n}}_{H} = (\begin{array}{c} 2 \\ 1 \\ 2 \end{array})$
  Sein Betrag ist $| {\vec{n}}_{H} | = \sqrt{2^{2} + 1^{2} + 2^{2}} = \sqrt{4 + 1 + 4} = \sqrt{9} = 3$ .
  Da die Kantenlänge des Würfels $12$ ist, ist die Höhe einer Pyramide gleich $6$ .
  Da der Betrag des Normalenvektors $3$ beträgt, muss er zweimal zum Vektor $\vec{O M_{A C}}$ addiert werden, um zur Pyramidenspitze $S$ zu gelangen ( $h = 6 = 2 \cdot | {\vec{n}}_{H} |$ ).
  Dann folgt für den Vektor $\vec{O S}$ :
  $\vec{O S} = \vec{O M_{A C}} + 2 \cdot {\vec{n}}_{H} = (\begin{array}{c} - 1 \\ - 2 \\ 5 \end{array}) + 2 \cdot (\begin{array}{c} 2 \\ 1 \\ 2 \end{array}) = (\begin{array}{c} - 1 + 4 \\ - 2 + 2 \\ 5 + 4 \end{array}) = (\begin{array}{c} 3 \\ 0 \\ 9 \end{array})$
  Der eine Eckpunkt $S$ des Oktaeders hat die Koordinaten $S (3 | 0 | 9)$ .
  Ergänzung (nicht in der Aufgabenstellung gefordert):
  Der andere Eckpunkt $S^{'}$ , der nicht in $H$ liegt, ist dann:
  $\vec{O S^{'}} = \vec{O M_{A C}} - 2 \cdot {\vec{n}}_{H} = (\begin{array}{c} - 1 \\ - 2 \\ 5 \end{array}) - 2 \cdot (\begin{array}{c} 2 \\ 1 \\ 2 \end{array}) = (\begin{array}{c} - 1 - 4 \\ - 2 - 2 \\ 5 - 4 \end{array}) = (\begin{array}{c} - 5 \\ - 4 \\ 1 \end{array})$
  Der andere Eckpunkt des Oktaeders $S^{'}$ hat die Koordinaten $S^{'} (- 5 | - 4 | 1)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme den Mittelpunkt von $A C$ $\Rightarrow \vec{O M_{A C}}$
  Lies den Normalenvektor der Ebene $H$ ab und berechne seinen Betrag.
  Da die Kantenlänge des Würfels $12$ ist, ist die Höhe einer Pyramide gleich $6$ .
  Überlege Dir, wie oft der Normalenvektor zum Vektor $\vec{O M_{A C}}$ addiert werden muss, um die Spitze $S$ der oberen Pyramide zu erreichen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Geometrie, Teil A, Aufgabengruppe 2

Die Kantenlänge des Würfels soll 12 betragen

Hast du eine Frage oder Feedback?

Die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in H liegen.

Hast du eine Frage oder Feedback?