Zwischen dem Alter einer Eiche in Jahren und ihrem Stammdurchmesser in Metern besteht ein funktionaler Zusammenhang , der modellhaft durch die Gleichung beschrieben ist. Der Schnitt durch den Stamm der Eiche wird dabei näherungsweise als Kreis angenommen. Der Durchmesser wird in einer Höhe von über dem Boden gemessen. Die Abbildung zeigt den Graphen der Funktion mit der Definitionsmenge .
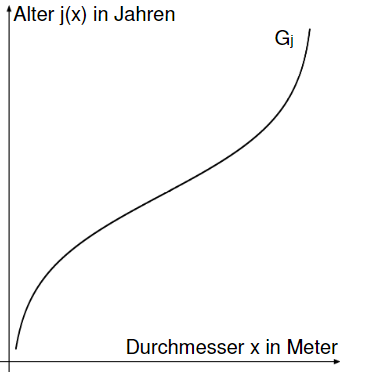
Der Graph der Funktion besitzt einen Wendepunkt. Die Altersangaben sind auf ganze Jahre zu runden. Auf die Mitführung von Einheiten kann verzichtet werden.
Bestimmen Sie das Alter einer Eiche, wenn in einer Höhe von der Umfang des Stammes beträgt.
Ermitteln Sie die Wertemenge der Funktion - auch unter Verwendung des Graphen von 3) - und interpretieren Sie Ihr Ergebnis im Sachzusammenhang.
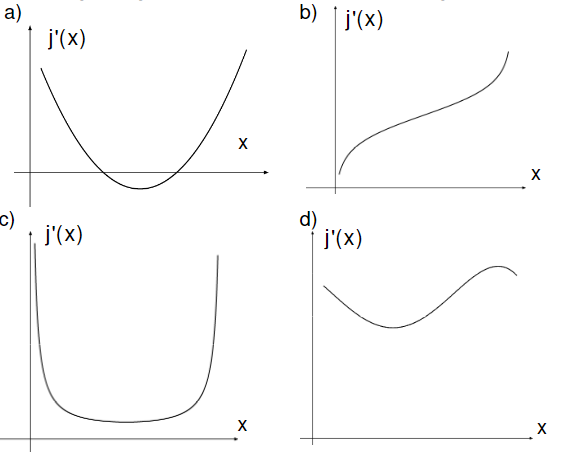
Eine der folgenden vier Abbildungen zeigt den Graphen der ersten Ableitungsfunktion . Geben Sie den Buchstaben des richtigen Graphen an und stützen Sie Ihre Wahl durch ein bekräftigendes Argument. Begründen Sie für jeden anderen Graphen mit einem stichhaltigen Argument, warum dieser nicht in Frage kommt.
Gegeben ist die Gleichung der zweiten Ableitung der Funktion (Nachweis nicht erforderlich!). Berechnen Sie die Koordinaten des Wendepunktes von und erläutern Sie die Bedeutung im Sachzusammenhang.
