Aufgabe Q1
Gegeben ist für jede positive reelle Zahl 𝑎 die in definierte Funktion mit .
Die Abbildung zeigt den Graphen von sowie die Tangente 𝑡 an den Graphen von
im Punkt
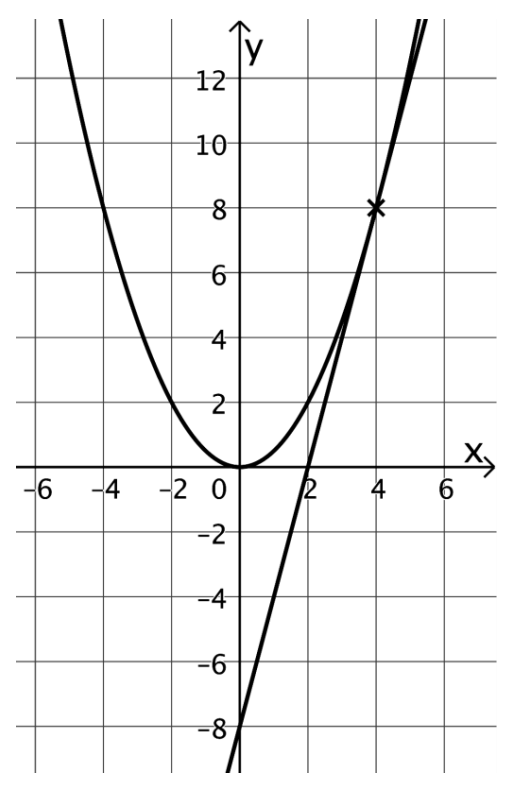
Geben Sie anhand der Abbildung eine Gleichung der Tangente 𝑡 an. [1 BE]
Weisen Sie nach, dass für jeden Wert die Tangente an den Graphen von im Punkt die 𝑦-Achse im Punkt schneidet. [4 BE]
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
serlo.orgDieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
→ Was bedeutet das?
