Wahlteil - CAS - lernen mit Serlo!

Aufgabe 3B

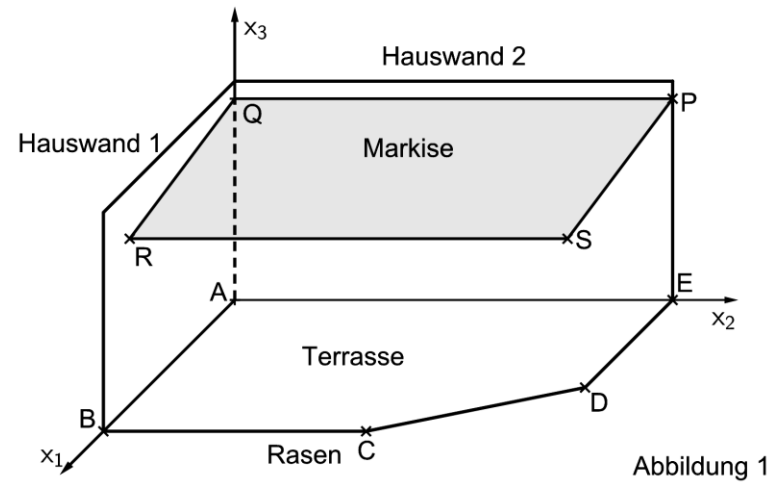
Abbildung 1 zeigt modellhaft eine Terrasse,

die von zwei Hauswänden und einer Rasenfläche begrenzt wird.

Ebenfalls dargestellt ist ein ausfahrbares

Sonnendach, im Folgenden als Markise

bezeichnet.

Der horizontale Boden, zu dem die Terrasse und die Rasenfläche gehören, wird im abgebildeten Koordinatensystem durch die $x_{1} x_{2}$ -Ebene dargestellt.

Die Terrasse wird durch das Fünfeck mit den Eckpunkten $A (0 | 0 | 0)$ , $B (3 | 0 | 0)$ , $C (3 | 3 | 0)$ , $D (2 | 5 | 0)$ und $E (0 | 5 | 0)$ beschrieben. Eine Längeneinheit im Koordinatensystem entspricht dabei $1 m$ in der Realität.

Bestimmen Sie die Gesamtlänge der an die Terrasse angrenzenden Rasenkanten sowie
den Flächeninhalt der Terrasse. [6 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
Bestimme die Gesamtlänge der an die Terrasse angrenzenden Rasenkanten
$l = | \vec{B C} | + | \vec{C D} | + | \vec{D E} |$
Berechne die Vektoren und ihre Beträge:
$\vec{B C} = \vec{O C} - \vec{O B} = (\begin{array}{c} 3 \\ 3 \\ 0 \end{array}) - (\begin{array}{c} 3 \\ 0 \\ 0 \end{array}) = (\begin{array}{c} 0 \\ 3 \\ 0 \end{array})$
$| \vec{B C} | = 3$
$\vec{C D} = \vec{O D} - \vec{O C} = (\begin{array}{c} 2 \\ 5 \\ 0 \end{array}) - (\begin{array}{c} 3 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array})$
$| \vec{C D} | = \sqrt{(- 1)^{2} + 2^{2} + 0} = \sqrt{5}$
$\vec{D E} = \vec{O E} - \vec{O D} = (\begin{array}{c} 0 \\ 5 \\ 0 \end{array}) - (\begin{array}{c} 2 \\ 5 \\ 0 \end{array}) = (\begin{array}{c} - 2 \\ 0 \\ 0 \end{array})$
$| \vec{D E} | = 2$
Dann folgt: $l = 3 + \sqrt{5} + 2 = 5 + \sqrt{5} \approx 7,24$
Die Gesamtlänge der an die Terrasse angrenzenden Rasenkanten beträgt rund $7,24 m$ .
Bestimme den Flächeninhalt der Terrasse
Zerlege die Fläche in ein Quadrat mit der Seitenlänge $3$ und ein Trapez.
Siehe Skizze:
Dann erhält man für den Flächeninhalt der Terrasse:
$A = A_{Quadrat} + A_{Trapez} = 3 \cdot 3 + \frac{3 + 2}{2} \cdot 2 = 9 + 5 = 14$
Der Flächeninhalt der Terrasse beträgt $14 m^{2}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Berechne $l = | \vec{B C} | + | \vec{C D} | + | \vec{D E} |$ .
Teil 2
Zerlege die Fläche in ein Quadrat mit der Seitenlänge $3$ und ein Trapez.
Die Befestigung der Markise an der Hauswand $2$ hat die Endpunkte $P (0 | 5 | 2,3)$ und
$Q (0 | 0 | 2,3)$ .
Ist die Markise vollständig ausgefahren, sind ihre weiteren Eckpunkte $R (2,4 | 0 | 1,9)$ und $S (2,4 | 5 | 1,9)$ . Die Markise ist rechteckig und liegt im Modell in der Ebene $M$ mit der Gleichung $x_{1} + 6 x_{3} = 13,8$ .
Das zu einem bestimmten Zeitpunkt auf die Terrasse einfallende Sonnenlicht wird durch
parallele Geraden mit dem Richtungsvektor $(\begin{array}{c} - 0,92 \\ 0 \\ - 2 \end{array})$ beschrieben.
Untersuchen Sie, ob zu diesem Zeitpunkt bei vollständig ausgefahrener Markise mehr als die Hälfte der Terrassenfläche im Schatten liegt. [7 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
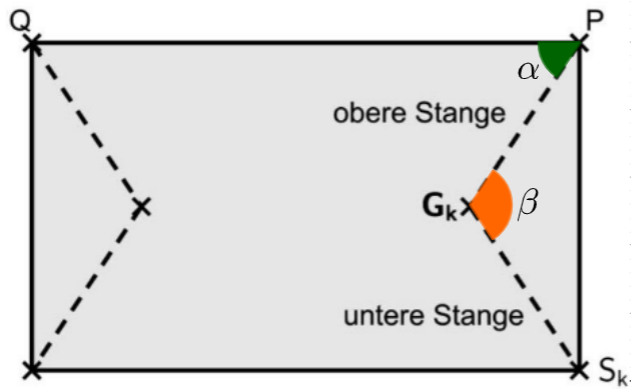
Untersuche, ob zu diesem Zeitpunkt bei vollständig ausgefahrener Markise mehr als die Hälfte der Terrassenfläche im Schatten liegt
Der Lichteinfall erfolgt parallel zur Hauswand $1$ . Der Schatten von $R S$ liegt also parallel zu Hauswand $2$ und ist die Begrenzungslinie des Schattens auf der Terrasse.
Berechne den Schattenpunkt $R^{'}$ von $R$ .
Erstelle dazu eine Geradengleichung durch den Punkt R mit dem Richtungsvektor ${\vec{v}}_{Licht}$ .
$g_{Licht} : \vec{x} = \vec{O R} + r \cdot {\vec{v}}_{Licht} = (\begin{array}{c} 2,4 \\ 0 \\ 1,9 \end{array}) + r \cdot (\begin{array}{c} - 0,92 \\ 0 \\ - 2 \end{array})$
Schneide $g_{Licht}$ mit der $x_{1} x_{2}$ -Ebene, d.h. $x_{3} = 0$ :
$\Rightarrow 0 = 1,9 - 2 \cdot r \Rightarrow r = 0,95$
$r = 0,95$ eingesetzt in $g_{Licht}$ :
${\vec{x}}_{R^{'}} = (\begin{array}{c} 2,4 \\ 0 \\ 1,9 \end{array}) + 0,95 \cdot (\begin{array}{c} - 0,92 \\ 0 \\ - 2 \end{array}) = (\begin{array}{c} 2,4 + 0,95 \cdot (- 0,92) \\ 0 \\ 1,9 + 0,95 \cdot (- 2) \end{array}) = (\begin{array}{c} 1,526 \\ 0 \\ 0 \end{array})$
Der Terrassenpunkt $R^{'}$ hat die Koordinaten $R^{'} (1,526 | 0 | 0)$ .
Die Terrasse liegt also bis zu einem Abstand von $1,526 m$ von Hauswand $2$ im
Schatten. Da jeder Punkt der Terrasse maximal $3 m$ von Hauswand $2$ entfernt
ist, liegt mehr als die Hälfte der Terrasse im Schatten.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Lichteinfall erfolgt parallel zur Hauswand $1$ . Der Schatten von $R S$ liegt also parallel zu Hauswand $2$ und ist die Begrenzungslinie des Schattens auf der Terrasse.
Berechne den Schattenpunkt $R^{'}$ von $R$ . Erstelle dazu eine Geradengleichung durch den Punkt R mit dem Richtungsvektor ${\vec{v}}_{Licht}$ .
Die Koordinaten von $R^{'}$ sagen etwas darüber aus, wie weit der Schatten von Hauswand 2 aus reicht.
Abbildung $2$ zeigt die Oberseite der Markise mit ihren beiden gestrichelt dargestellten Gelenkarmen. Der rechte Gelenkarm besteht aus der oberen Stange $P G_{k}$ , einem Gelenk im Punkt $G_{k}$ und einer unteren Stange $G_{k} S_{k}$ .
Die obere und die untere Stange
sind gleich lang. Beim Ausfahren der Markise verändern sich die Positionen der Punkte $G_{k}$ und $S_{k}$ .
Die obere Stange wird beschrieben durch $o_{k} : \vec{x} = (\begin{array}{c} 0 \\ 5 \\ 2,3 \end{array}) + λ \cdot (\begin{array}{c} 2,4 k \\ - 0,8 \\ - 0,4 k \end{array})$ mit $λ \in ℝ$ und $0,04 \leq k \leq 1$ .
Je größer $k$ ist, desto weiter ist die Markise ausgefahren. Für $k = 1$ ist sie vollständig
ausgefahren und für $k = 0,04$ ist sie vollständig eingefahren.
Zeigen Sie, dass alle Geraden $o_{k}$ in der Ebene $M$ mit $x_{1} + 6 x_{3} = 13,8$ liegen. [4 BE]
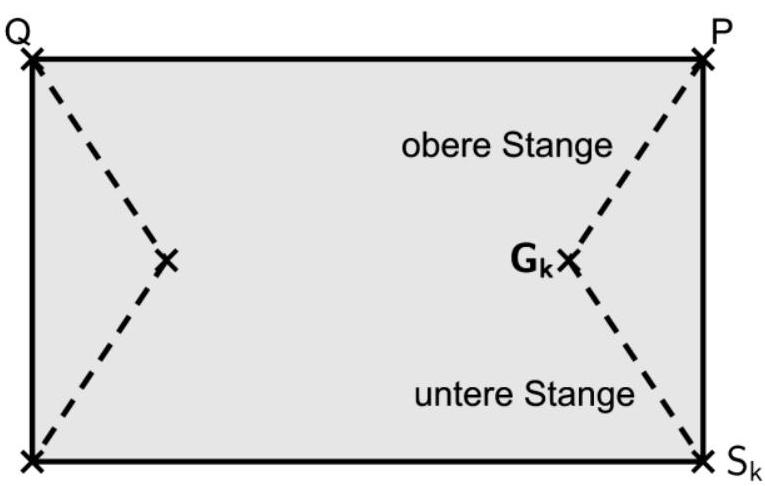
Abbildung 2
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen
Zeige, dass alle Geraden $o_{k}$ in der Ebene $M$ mit $x_{1} + 6 x_{3} = 13,8$ liegen
Gegeben sind $o_{k} : \vec{x} = (\begin{array}{c} 0 \\ 5 \\ 2,3 \end{array}) + λ \cdot (\begin{array}{c} 2,4 k \\ - 0,8 \\ - 0,4 k \end{array})$ und $M : x_{1} + 6 \cdot x_{3} = 13,8$
Berechne $o_{k} \cap M$ :
$x_{1} + 6 \cdot x_{3}$ $=$ $13,8$
↓
Setze $o_{k}$ ein.
$0 + λ \cdot 2,4 k + 6 \cdot (2,3 - λ \cdot 0,4 k)$ $=$ $13,8$
↓
Löse die Klammer auf.
$λ \cdot 2,4 k + 13,8 - λ \cdot 2,4 k)$ $=$ $13,8$
↓
Fasse zusammen.
$13,8$ $=$ $13,8$
Du hast eine wahre Aussage erhalten, d.h. alle Geraden $o_{k}$ liegen in der Ebene $M$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $o_{k} \cap M$ .
Die folgende Rechnung liefert die Größen zweier Winkel:
$\cos (α) = \frac{| (\begin{array}{c} 0 \\ 1 \\ 0 \end{array}) \circ (\begin{array}{c} 2,4 \\ - 0,8 \\ - 0,4 \end{array}) |}{| (\begin{array}{c} 0 \\ 1 \\ 0 \end{array}) | \cdot | (\begin{array}{c} 2,4 \\ - 0,8 \\ - 0,4 \end{array}) |}$ liefert $α \approx {71,8}^{\circ}$ und damit $β = 2 \cdot α \approx {143,6}^{\circ}$ .
Geben Sie die Bedeutung von $α$ und $β$ im Sachzusammenhang an. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Gib die Bedeutung von $α$ und $β$ im Sachzusammenhang an
Der Vektor $(\begin{array}{c} 0 \\ 1 \\ 0 \end{array})$ zeigt in Richtung der $x_{2}$ -Achse (hintere Markisenkante).
Der Vektor $(\begin{array}{c} 2,4 \\ - 0,8 \\ - 0,4 \end{array})$ ist der Richtungsvektor der oberen Stange für $k = 1$ , d.h. bei ausgefahrener Markise. Der Winkel zwischen diesen beiden Vektoren ist der Winkel $α$ , der berechnet wird und mit dem Winkel $α$ wird der Winkel $β$ berechnet.
Deshalb gilt bei vollständig ausgefahrener Markise:
$α$ ist die Größe des Winkels zwischen der hinteren Kante der Markise und der oberen Stange.
$β$ ist die Größe des Winkels zwischen den beiden Stangen des Gelenkarms.
Siehe Skizze:
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Vektor $(\begin{array}{c} 0 \\ 1 \\ 0 \end{array})$ zeigt in Richtung der $x_{2}$ -Achse (hintere Markisenkante).
Der Vektor $(\begin{array}{c} 2,4 \\ - 0,8 \\ - 0,4 \end{array})$ ist der Richtungsvektor der oberen Stange für $k = 1$ , d.h. bei ausgefahrener Markise.
Sowohl die obere als auch die untere Stange des Gelenkarms sind $1,28 m$ lang.
Bestimmen Sie die Koordinaten von $G_{k}$ für $k = 0,5$ . [5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie
Bestimme die Koordinaten von $G_{k}$ für $k = 0,5$
Für $k = 0,5$ folgt $o_{0,5}$ :
$o_{0,5} : \vec{x} = (\begin{array}{c} 0 \\ 5 \\ 2,3 \end{array}) + λ \cdot (\begin{array}{c} 2,4 \cdot 0,5 \\ - 0,8 \\ - 0,4 \cdot 0,5 \end{array}) = (\begin{array}{c} 0 \\ 5 \\ 2,3 \end{array}) + λ \cdot (\begin{array}{c} 1,2 \\ - 0,8 \\ - 0,2 \end{array})$
Der Richtungsvektor von $o_{0,5}$ hat die Länge:
$| (\begin{array}{c} 1,2 \\ - 0,8 \\ - 0,2 \end{array}) | = \sqrt{{1,2}^{2} + (- 0,8)^{2} + (- 0,2)^{2}} = \sqrt{2,12} \approx 1,46$
Dann folgt:
$\vec{x} \approx (\begin{array}{c} 0 \\ 5 \\ 2,3 \end{array}) + \frac{λ_{1}}{1,46} \cdot (\begin{array}{c} 1,2 \\ - 0,8 \\ - 0,2 \end{array})$
Sowohl die obere als auch die untere Stange des Gelenkarms sind $1,28 m$ lang.
$G_{0,5}$ liegt auf $𝑜_{0,5}$ und hat mit $λ_{1} = 1,28$ die Koordinaten:
$\vec{x} \approx (\begin{array}{c} 0 \\ 5 \\ 2,3 \end{array}) + \frac{1,28}{1,46} \cdot (\begin{array}{c} 1,2 \\ - 0,8 \\ - 0,2 \end{array}) = (\begin{array}{c} 0 \\ 5 \\ 2,3 \end{array}) + \frac{1,28}{1,46} \cdot (\begin{array}{c} 1,2 \\ - 0,8 \\ - 0,2 \end{array})$
$\vec{x} \approx (\begin{array}{c} 0 \\ 5 \\ 2,3 \end{array}) + \frac{1,28}{1,46} \cdot (\begin{array}{c} 1,2 \\ - 0,8 \\ - 0,2 \end{array}) \approx (\begin{array}{c} 0 \\ 5 \\ 2,3 \end{array}) + (\begin{array}{c} 1,05 \\ - 0,70 \\ - 0,18 \end{array}) = (\begin{array}{c} 1,05 \\ 4,30 \\ 2,12 \end{array})$
Die gesuchten Koordinaten von $G_{0,5}$ sind etwa $(1,05 | 4,30 | 2,12)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme die Gleichung von $o_{0,5}$ und berechne die Länge des Richtungsvektors dieser Geraden.
Schreibe die Geradengleichung mit einem Einheitsrichtungsvektor.
$G_{0,5}$ liegt auf $𝑜_{0,5}$ . Beachte, dass die obere als auch die untere Stange des Gelenkarms $1,28 m$ lang sind.
Ersetze den Parameter in der Geradengleichung mit einem Einheitsrichtungsvektor durch $1,28$ und berechne die gesuchten Koordinaten.

Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen → Was bedeutet das?

$x_{1} + 6 \cdot x_{3}$	$=$	$13,8$
	↓	Setze $o_{k}$ ein.
$0 + λ \cdot 2,4 k + 6 \cdot (2,3 - λ \cdot 0,4 k)$	$=$	$13,8$
	↓	Löse die Klammer auf.
$λ \cdot 2,4 k + 13,8 - λ \cdot 2,4 k)$	$=$	$13,8$
	↓	Fasse zusammen.
$13,8$	$=$	$13,8$

Aufgabe 3B

Bestimme die Gesamtlänge der an die Terrasse angrenzenden Rasenkanten

Bestimme den Flächeninhalt der Terrasse

Hast du eine Frage oder Feedback?

Untersuche, ob zu diesem Zeitpunkt bei vollständig ausgefahrener Markise mehr als die Hälfte der Terrassenfläche im Schatten liegt

Hast du eine Frage oder Feedback?

Zeige, dass alle Geraden ok in der Ebene M mit x1+6x3=13,8 liegen

Hast du eine Frage oder Feedback?

Gib die Bedeutung von α und β im Sachzusammenhang an

Hast du eine Frage oder Feedback?

Bestimme die Koordinaten von Gk für k=0,5

Hast du eine Frage oder Feedback?

Zeige, dass alle Geraden $o_{k}$ in der Ebene $M$ mit $x_{1} + 6 x_{3} = 13,8$ liegen

Gib die Bedeutung von $α$ und $β$ im Sachzusammenhang an

Bestimme die Koordinaten von $G_{k}$ für $k = 0,5$