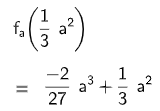Wahlteil - CAS
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Aufgabe 1A
Gegeben ist die Schar der in definierten Funktionen mit
und .
Skizzieren Sie den Graphen von in Abbildung 1.
Geben Sie die Extrempunkte von an. [5BE]
Ermitteln Sie die Koordinaten der gemeinsamen Punkte der Graphen von und .
Weisen Sie nach, dass es nur einen Punkt gibt, der auf allen Graphen der Schar liegt.
[5 BE]
Die Gleichung hat in Abhängigkeit von die Lösungen und und .
Geben Sie die Anzahl der Nullstellen von in Abhängigkeit von an und begründen Sie Ihre Angabe anhand der obigen Terme. [6 BE]
Der Graph jeder Funktion hat genau einen Wendepunkt .
Bestimmen Sie den Wert von zu dem Wendepunkt mit der größten y-Koordinate. [5 BE]
Für ein Umweltschutzprojekt nehmen zwei Unterwasserdrohnen und in einem See Messungen in unterschiedlichen Tiefen vor. Sie bewegen sich nur in vertikaler Richtung, d.h. senkrecht zur Wasseroberfläche des Sees. Ihre Geschwindigkeiten werden für durch die in definierten Funktionen bzw. beschrieben, wobei gilt:
und
Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Minuten. ist die
Geschwindigkeit von in Meter pro Minute und ist die Geschwindigkeit von in Meter pro Minute. Wenn die Geschwindigkeit positiv ist, steigt die Unterwasserdrohne.
Bestimmen Sie die Koordinaten des Tiefpunktes des Graphen von und
interpretieren Sie die Werte im Sachkontext. [4 BE]
Mit wird die erste Ableitungsfunktion von bezeichnet. Innerhalb eines bestimmten
Zeitraums gilt für jeden Zeitpunkt die folgende Aussage: und
Interpretieren Sie dies in Bezug auf die Bewegung von in diesem Zeitraum. [3 BE]
Im Beobachtungszeitraum beträgt der geringste Abstand von zur Wasseroberfläche
des Sees Meter.
Ermitteln Sie den Abstand von zur Wasseroberfläche zu Beobachtungsbeginn. [6 BE]
ist zu Beobachtungsbeginn Meter tiefer als und steigt langsamer als .
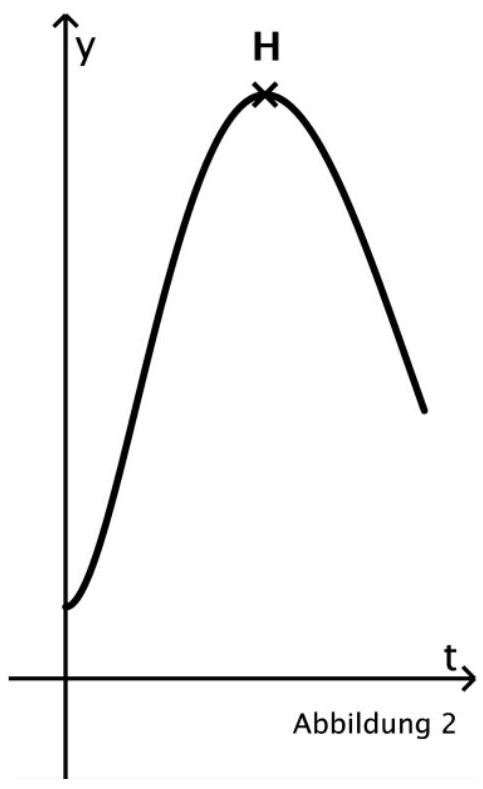
Der Graph in Abbildung 2 zeigt für die ersten Minuten des Beobachtungszeitraums die zeitliche Entwicklung des vertikalen Abstands der beiden Unterwasserdrohnen zueinander.
Im dargestellten Bereich hat der Graph nur einen Hochpunkt .
Erläutern Sie, wie man anhand der Graphen von und ermitteln
kann, und geben Sie einen Term zur Berechnung von an. [6 BE]
- 2
Aufgabe 1B
Die zeitliche Entwicklung der Blutalkoholkonzentration (BAK) kann für eine bestimmte
Person nach dem Verzehr von zwei Gläsern Wein durch die auf definierte Funktion
mit beschrieben werden. Dabei gibt die Zeit nach dem
Trinken in Stunden an und die BAK in Gramm pro Kilogramm . Es soll vereinfacht
davon ausgegangen werden, dass die gesamte Menge Wein auf einmal konsumiert wird.
Geben Sie die Nullstellen von an.
Begründen Sie, dass das Intervall eine angemessene Einschränkung des
Definitionsbereichs der Funktion für den Sachzusammenhang ist. [3 BE]
Berechnen Sie die maximale BAK der betrachteten Person.
Bei einer BAK von oder mehr darf die Person in Deutschland kein Auto mehr fahren.
Bestimmen Sie den Zeitraum, in dem die Person nicht Auto fahren darf. [6 BE]
Mit Hilfe einer linearen Funktion können Näherungswerte für die BAK berechnet werden.
Für jede Person ergibt sich je nach individuellen Eigenschaften und konsumierter
Alkoholmenge eine andere lineare Funktion.
Der y-Achsenabschnitt des Graphen der linearen Funktion wird als theoretische maximale BAK bezeichnet.
Für die betrachtete Person wird die auf definierte Funktion mit verwendet. Dabei beschreibt die Zeit nach dem Trinken in Stunden und Näherungswerte der BAK in .
Zeigen Sie, dass die theoretische maximale BAK für die betrachtete Person beträgt.
Zur Bestimmung der linearen Funktion für eine zweite Person werden zwei Messungen durchgeführt: Stunden nach dem Verzehr beträgt die BAK und weitere Minuten später .
Berechnen Sie damit die theoretische maximale BAK der zweiten Person. [5 BE]
Begründen Sie mit Hilfe des Terms von , dass die Werte der BAK der ersten
betrachteten Person zu jedem Zeitpunkt kleiner sind als ihre theoretische maximale
BAK. [3 BE]
Zeigen Sie, dass eine Lösung der Differenzialgleichung
mit , und ist. [4 BE]
Für verschiedene Personen ergeben sich individuelle zeitliche Verläufe der BAK.
Für werden die auf definierten Funktionen mit
betrachtet.
beschreibt die Zeit nach dem Trinken in Stunden und die BAK in .
Bestimmen Sie alle Werte von so, dass die BAK zu keinem Zeitpunkt den Wert von überschreitet. [7 BE]
Unabhängig vom Sachkontext wird für die auf definierte Funktionenschar betrachtet mit .
Zeigen Sie, dass jede Funktion der Schar ein lokales Maximum an der Stelle
hat.
Begründen Sie, dass die x-Koordinaten der Hochpunkte mit wachsenden Werten von kleiner werden. [7 BE]
Der Inhalt der Fläche zwischen den Graphen von und auf dem Intervall soll
an der Stelle durch eine Parallele zur y-Achse halbiert werden.
Bestimmen Sie . [5 BE]
- 3
Aufgabe 2A
Ein Institut für Ernährungsforschung untersucht die Essgewohnheiten von in Deutschland lebenden Personen einer bestimmten Altersgruppe. Im Folgenden wird davon ausgegangen, dass sich der Personen der betrachteten Gruppe häufig von Fertiggerichten ernähren.
Es werden Personen der betrachteten Gruppe zufällig ausgewählt.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass sich mindestens ein Viertel dieser
Personen häufig von Fertiggerichten ernährt. [3 BE]
Beschreiben Sie im Sachzusammenhang ein Zufallsexperiment, bei dem die
Wahrscheinlichkeit eines Ereignisses mit dem Term
berechnet werden kann. Geben Sie dieses Ereignis an. [4 BE]
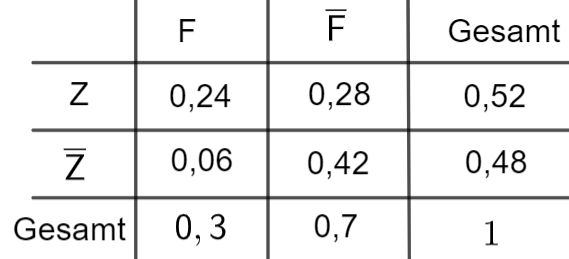
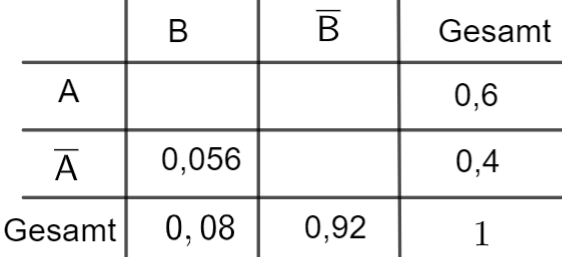
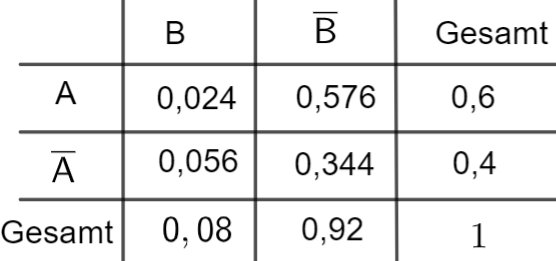
Neben der Ernährung durch Fertiggerichte wird auch der Verzehr von Zucker untersucht. Der Anteil der Personen der betrachteten Gruppe, die sich häufig von Fertiggerichten ernähren und zu viel Zucker verzehren, beträgt .
Der Anteil der Personen, die zu viel Zucker verzehren, ist unter denjenigen, die sich häufig von Fertiggerichten ernähren, doppelt so groß wie unter denjenigen, die sich nicht häufig von Fertiggerichten ernähren. Aus der betrachteten Gruppe wird eine Person zufällig ausgewählt.
Untersucht werden folgende Ereignisse:
: „Die Person ernährt sich häufig von Fertiggerichten.“
: „Die Person verzehrt zu viel Zucker.“
Weisen Sie nach, dass die Wahrscheinlichkeit dafür, dass die ausgewählte Person zu viel
Zucker verzehrt und sich nicht häufig von Fertiggerichten ernährt, beträgt. [4 BE]
Stellen Sie den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar. [3 BE]
Das Institut untersucht den Anteil der Personen der betrachteten Gruppe, die einen
bestimmten zuckerfreien Müsliriegel gegenüber einem vergleichbaren zuckerhaltigen
Müsliriegel bevorzugen.
Aufgrund früherer Untersuchungen wird von einem Anteil von ausgegangen.
Bei einer Umfrage unter Personen der
betrachteten Gruppe gaben Personen an, den zuckerfreien Müsliriegel zu bevorzugen.
Abgebildet sind die Graphen der für
definierten Funktionen
und
.
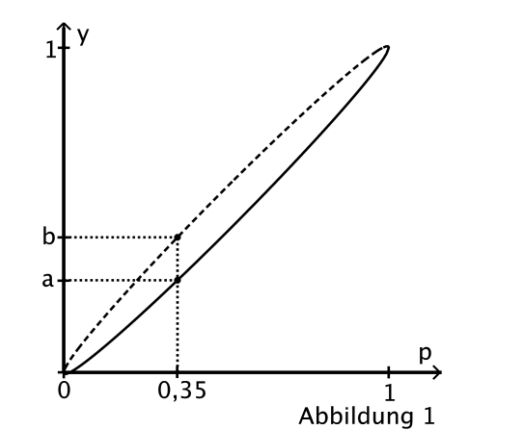
Geben Sie die Werte von und an.
Interpretieren Sie das Ergebnis der Umfrage im Hinblick auf die Bedeutung des Intervalls (vgl. Abbildung 1). [4 BE]
Nach der Durchführung einer Werbemaßnahme für den zuckerfreien Müsliriegel möchte das Institut Anhaltspunkte darüber gewinnen, wie groß der Anteil inzwischen ist.
In der betrachteten Gruppe wurden daraufhin Personen befragt.
Die Auswertung ergab, dass etwa der befragten Personen den zuckerfreien Riegel bevorzugen. Das zugehörige -Konfidenzintervall, dessen Ränder mit den Gleichungen
und
ermittelt werden, besitzt eine Länge, die kleiner als ist.
Zeigen Sie, dass der kleinstmögliche Wert von zwischen und liegt. [7 BE]
- 4
Aufgabe 2B
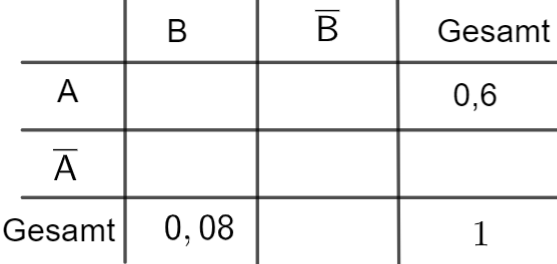
Bei einer statistischen Erhebung werden in einer deutschen Großstadt die privaten
Haushalte mit mindestens einem Kind im Vorschulalter betrachtet. Diese werden im
Folgenden als „junge Haushalte“ bezeichnet. Es wird festgestellt, dass der jungen
Haushalte mit mindestens einem Pkw ausgestattet sind und der jungen Haushalte mit mindestens einem Lastenrad. In der jungen Haushalte ohne Pkw ist mindestens ein Lastenrad vorhanden.
Stellen Sie den beschriebenen Sachverhalt in einer vollständig ausgefüllten
Vierfeldertafel dar. [4 BE]
Beurteilen Sie für diese Großstadt die folgende Aussage: [4 BE]
Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter junger Haushalt mit mindestens einem Lastenrad ausgestattet ist, ist bei einem jungen Haushalt ohne Pkw mehr als dreimal so groß wie bei einem jungen Haushalt mit mindestens einem Pkw.
junge Haushalte dieser Großstadt werden zufällig ausgewählt.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass mehr als und höchstens dieser
Haushalte mit mindestens einem Lastenrad ausgestattet sind. [3 BE]
Geben Sie im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem
Term
berechnet werden kann. [3 BE]
Betrachtet werden Vorderrad- und Hinterradreifen für Lastenräder. Die Laufleistung gibt die Gesamtstrecke an, bis ein Reifen unbrauchbar wird. Die Zufallsgröße beschreibt die Laufleistung in Kilometern () der Vorderradreifen eines Herstellers, die Zufallsgröße die Laufleistung der Hinterradreifen desselben Herstellers. Beide Zufallsgrößen sind normalverteilt. Es gilt:
und
und
Bestimmen Sie die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter
Vorderradreifen eine Laufleistung hat, die um höchstens vom Erwartungswert
für diese Laufleistung abweicht. [3 BE]
Begründen Sie, dass die folgende Aussage für die Vorderrad- und Hinterradreifen wahr
ist: [4 BE]
Die Laufleistung, die ein zufällig ausgewählter Vorderradreifen gemäß dem Modell mit der Wahrscheinlichkeit von übertreffen wird, wird ein zufällig ausgewählter Hinterradreifen nahezu mit Sicherheit unterschreiten.
Die Zufallsgröße beschreibt die
Laufleistung in km der Hinterradreifen
eines anderen Herstellers.
wird als normalverteilt mit dem Erwartungswert und der Standardabweichung angenommen.
Die Abbildung stellt den Graphen der
Funktion mit dar.
Ermitteln Sie die Werte von und jeweils in km. [4 BE]
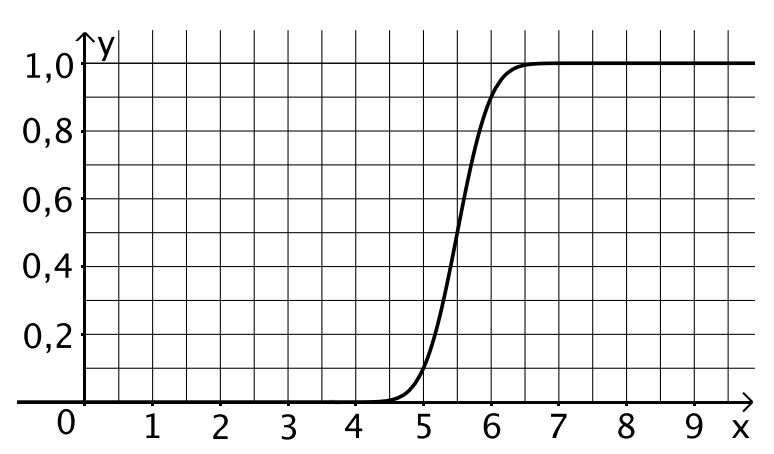
- 5
Aufgabe 3A
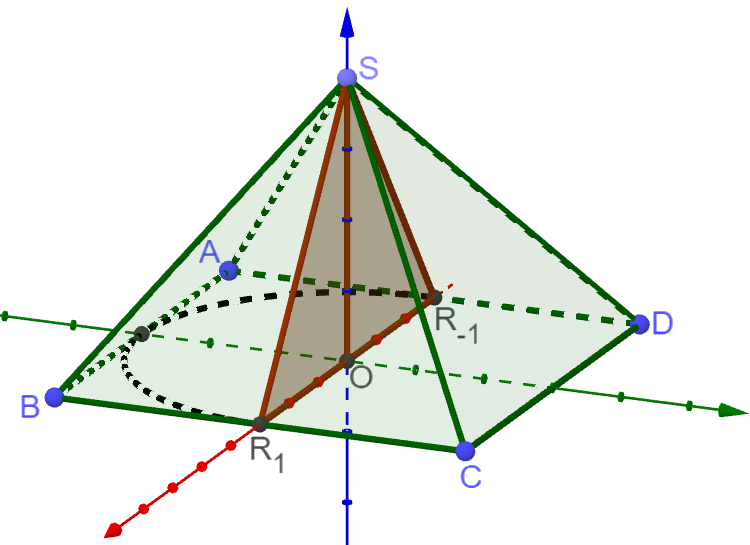
Abbildung 1 zeigt die Pyramide mit den Eckpunkten , ,
, und sowie den Punkt , der in der quadratischen Grundfläche der Pyramide liegt.
Die Seitenfläche der Pyramide liegt in der Ebene .
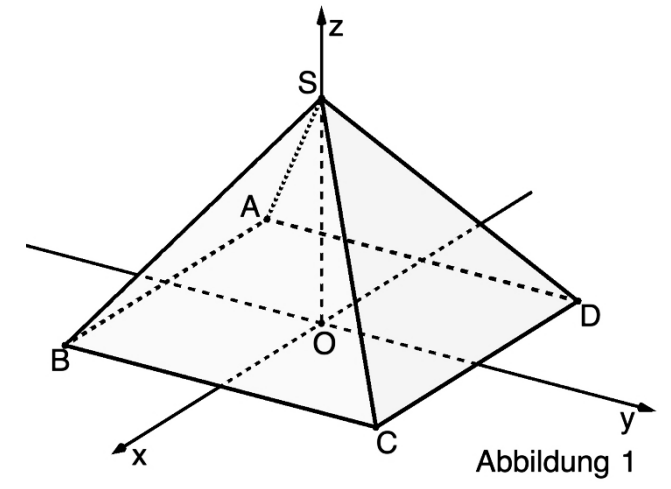
Berechnen Sie den Inhalt der Oberfläche der Pyramide. [4 BE]
Bestimmen Sie eine Gleichung von in Koordinatenform. [3 BE]
[Zur Kontrolle: ]
Es gibt einen Punkt , der im Innern der Pyramide liegt und von allen vier
Seitenflächen sowie der Grundfläche der Pyramide den gleichen Abstand hat. Mithilfe
des folgenden Gleichungssystems lässt sich der Wert von bestimmen:
Geben Sie die geometrische Bedeutung dieser Gleichungen an. [5 BE]
Die Ebene gehört zur Schar der Ebenen mit
. Die Seitenfläche der Pyramide liegt in der Ebene der Schar, die Seitenfläche in der Ebene .
Zeigen Sie, dass der Punkt in allen Ebenen der Schar enthalten ist. [2 BE]
Weisen Sie nach, dass die Größe des Winkels, unter dem die Gerade die Ebene
schneidet, unabhängig von ist. Bestimmen Sie die Größe dieses Winkels. [5 BE]
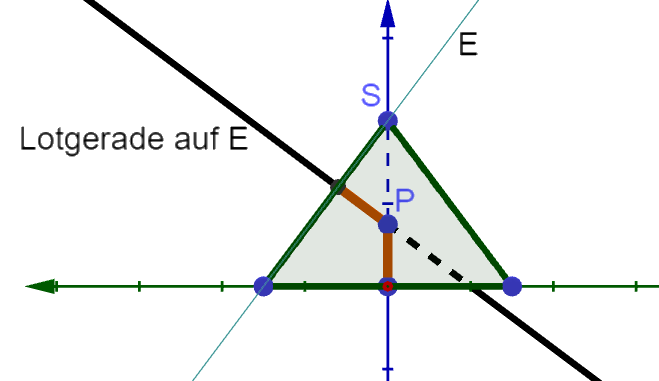
Jede Ebene der Schar schneidet die
xy-Ebene in einer Gerade . Mit wird jeweils derjenige Punkt auf bezeichnet, der von den kleinsten Abstand hat. In Abbildung 2 sind und beispielhaft für eine Ebene der Schar dargestellt.
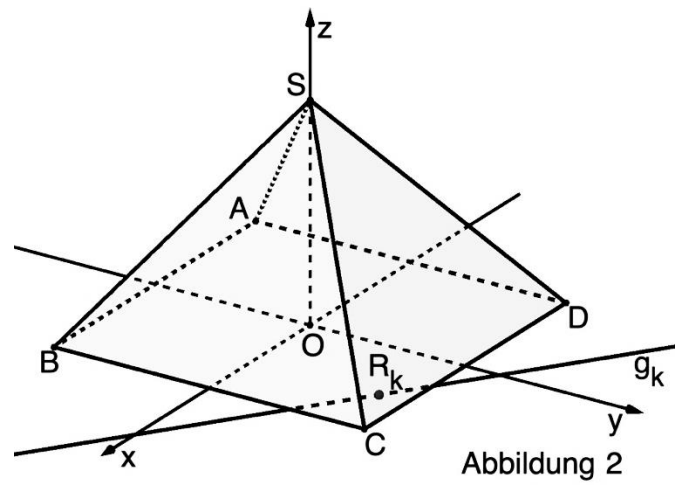
Zeichnen Sie die Punkte und in Abbildung 2 ein. [3 BE]
Durchläuft alle Werte von bis , dann dreht sich die Fläche um die Strecke . Dabei entsteht ein Körper. Beschreiben Sie die Form des entstehenden Körpers und bestimmen Sie das Volumen dieses Körpers. [3 BE]
- 6
Aufgabe 3B
Abbildung 1 zeigt modellhaft eine Terrasse,
die von zwei Hauswänden und einer Rasenfläche begrenzt wird.
Ebenfalls dargestellt ist ein ausfahrbares
Sonnendach, im Folgenden als Markise
bezeichnet.
Der horizontale Boden, zu dem die Terrasse und die Rasenfläche gehören, wird im abgebildeten Koordinatensystem durch die -Ebene dargestellt.
Die Terrasse wird durch das Fünfeck mit den Eckpunkten , , , und beschrieben. Eine Längeneinheit im Koordinatensystem entspricht dabei in der Realität.
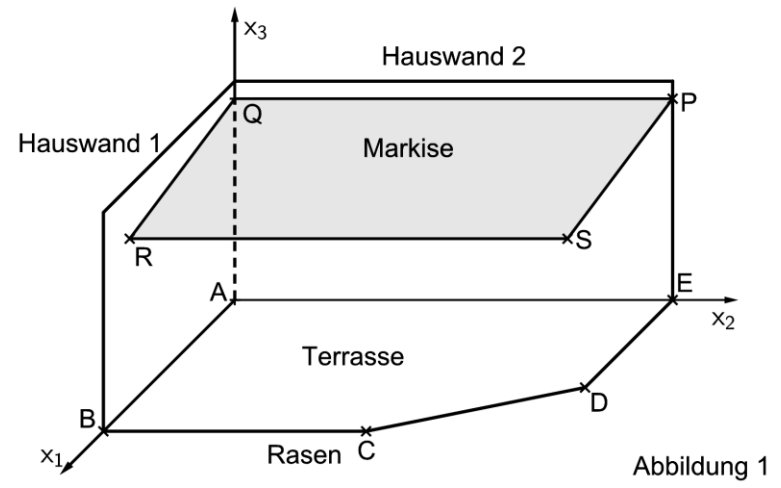
Bestimmen Sie die Gesamtlänge der an die Terrasse angrenzenden Rasenkanten sowie
den Flächeninhalt der Terrasse. [6 BE]
Die Befestigung der Markise an der Hauswand hat die Endpunkte und
.
Ist die Markise vollständig ausgefahren, sind ihre weiteren Eckpunkte und . Die Markise ist rechteckig und liegt im Modell in der Ebene mit der Gleichung .
Das zu einem bestimmten Zeitpunkt auf die Terrasse einfallende Sonnenlicht wird durch
parallele Geraden mit dem Richtungsvektor beschrieben.
Untersuchen Sie, ob zu diesem Zeitpunkt bei vollständig ausgefahrener Markise mehr als die Hälfte der Terrassenfläche im Schatten liegt. [7 BE]
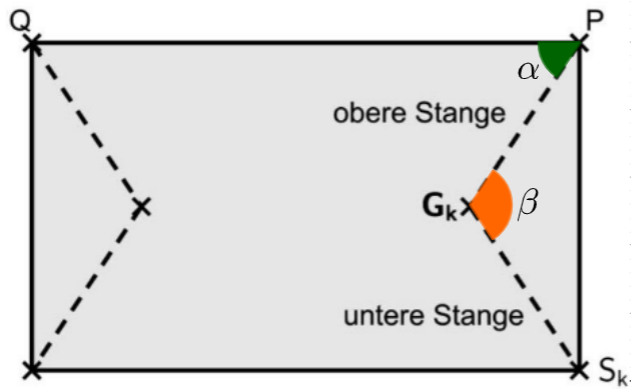
Abbildung zeigt die Oberseite der Markise mit ihren beiden gestrichelt dargestellten Gelenkarmen. Der rechte Gelenkarm besteht aus der oberen Stange , einem Gelenk im Punkt und einer unteren Stange .
Die obere und die untere Stange
sind gleich lang. Beim Ausfahren der Markise verändern sich die Positionen der Punkte und .
Die obere Stange wird beschrieben durch mit und .
Je größer ist, desto weiter ist die Markise ausgefahren. Für ist sie vollständig
ausgefahren und für ist sie vollständig eingefahren.
Zeigen Sie, dass alle Geraden in der Ebene mit liegen. [4 BE]
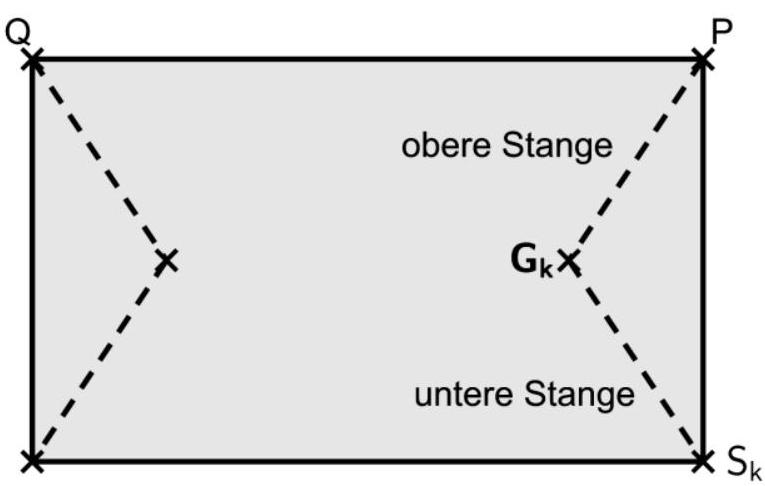
Abbildung 2
Die folgende Rechnung liefert die Größen zweier Winkel:
liefert und damit .
Geben Sie die Bedeutung von und im Sachzusammenhang an. [3 BE]
Sowohl die obere als auch die untere Stange des Gelenkarms sind lang.
Bestimmen Sie die Koordinaten von für . [5 BE]
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?