A I

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Gegeben ist die ganzrationale Funktion $f : x \mapsto \frac{1}{9} (- x^{4} + 4 x^{3})$ mit der Definitionsmenge $D_{f} = ℝ .$ Der Graph der Funktion $f$ wird mit $G_{f}$ bezeichnet.
1. Bestimmen Sie die Nullstellen der Funktion $f$ mit der jeweiligen Vielfachheit.
2. Ermitteln Sie die maximalen Monotonieintervalle der Funktion $f$ sowie Art und Koordinaten des Extrempunktes des Graphen $G_{f} .$
3. Bestimmen Sie die Gleichungen aller Wendetangenten an den Graphen $G_{f}$ .
4. Zeichnen Sie den Graphen $G_{f}$ unter Mitverwendung vorliegender Ergebnisse im Bereich $- 1 \leq x \leq 4$ in ein kartesisches Koordinatensystem. Für weitere Teilaufgaben wird auf der $y$ -Achse der Bereich $- 3 \leq y \leq 3$ benötigt.
  Maßstab: 1 LE = 1cm.
2
Betrachtet wird weiter die quadratische Funktion $p$ mit der Definitionsmenge $D_{p} = ℝ$ . Ihr Graph wird mit $G_{p}$ bezeichnet.
1. Die Parabel $G_{p}$ berührt den Graphen $G_{f}$ aus Aufgabe 1) im Punkt $B (3 | 3)$ und verläuft durch den Koordinatenursprung. Bestimmen Sie $p (x)$ und zeichnen Sie die Parabel $G_{p}$ im Bereich $- 1 \leq x \leq 4$ in das vorhandene Koordinatensystem ein.
  [ Mögliches Ergebnis: $p (x) = - \frac{1}{3} x^{2} + 2 x$ ]
2. Die Graphen $G_{f}$ und $G_{p}$ schließen im I. Quadranten des Koordinatensystems ein endli-ches Flächenstück ein. Markieren Sie dieses Flächenstück in Ihrer Zeichnung und berechnen Sie die Maßzahl seines Inhalts.
3. Berechnen Sie die Koordinaten desjenigen Schnittpunkts der Graphen $G_{f}$ und $G_{p}$ , der im III. Quadranten des Koordinatensystems liegt.
4. Bestimmen Sie die Steigungen der beiden Geraden durch den Punkt $T (3 | 4)$ , die den Graphen $G_{p}$ berühren.
3
Ein Bastler möchte sich mithilfe folgender Bauanleitung das Grundgerüst für einen zylinder-förmigen Abfallkorb mit Höhe $h$ und Radius $r$ (alle Längen in Meter gemessen) aus Draht bauen (siehe Skizze).
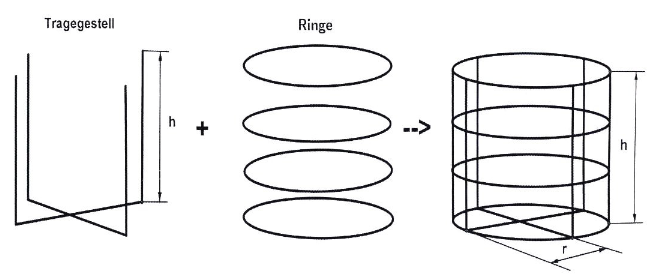
Für das Vorhaben kauft er sich Draht mit der Länge $6$ m. Die Einzelteile werden selbst her-gestellt und zusammengelötet. Die Dicke des Drahts ist zu vernachlässigen. Bei Berech-nungen kann auf Einheiten verzichtet werden.
1. Bestimmen Sie die Maßzahl $V (r)$ des Volumens des Abfallkorbs in Abhängigkeit von $r$ . [Mögliches Ergebnis: $V (r) = π (\frac{3}{2} r^{2} - r^{3} - 2 π r^{3})$ ]
2. Aus praktischen Gründen wird für die Funktion
  $V : r \mapsto V (r)$ als Definitionsmenge $D_{V} = [0,1; 0,2]$ gewählt.
  Berechnen Sie den Radius $r$ des Abfallkorbs für den Fall, dass die Maßzahl des Volumens ihren absolut größten Wert annimmt. Runden Sie Ihr Ergebnis auf drei Nachkommastellen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?