A I - lernen mit Serlo!

Gegeben ist die ganzrationale Funktion $g$ dritten Grades mit $D_g=\mathbb{R}$ , deren Graph $G_{g}$ in der Abbildung dargestellt ist.

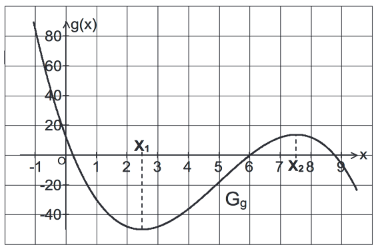
Vom Graphen sind folgende Eigenschaften bekannt: $G_{g}$ hat bei der Nullstelle $x = 6$ eine Tangente $G_{t}$ mit $t : y = 16 x - 96$ mit $x\in \mathbb{R}$ und besitzt den Wendepunkt $W (5 ∣ - 18) .$

Skizzieren Sie den Graphen $G_{g}$ der 1. Ableitungsfunktion von $g$ in ein geeignetes Koordi-natensystem und geben Sie die max. Monotonieintervalle der 1. Ableitungsfunktion $g^{'}$ an.
Zur Bestimmung des Funktionsterms $g (x)$ ist folgendes Gleichungssystem gegeben:
(I) $216 a + 36 b + 6 c + d = 0$
(II) $125 a + 25 b + 5 c + d = - 18$
(III) $108 a + 12 b + c = 16$
(IV) $30 a + 2 b = 0$
$1.$ Geben Sie nachvollziehbar an, welche Ansätze zu diesen Gleichungen führen.
$2.$ Bestimmen Sie $g (x)$ mithilfe der Gleichungen aus 1.b.