Nachtermin Teil B

Kreuze an, um wie viel Prozent die Anzahl der Kegelrobben im Wattenmeer laut der Funktion $f$ pro Jahr zunimmt

Der Wachstumsfaktor ist hier $a=\mathrm{1,1}$.

Es gilt: $a=1+p\Rightarrow p=\mathrm{0,1}$ oder $p=10\%$.

Die Anzahl der Kegelrobben im Wattenmeer nimmt laut der Funktion $f$ pro Jahr um $10\%$ zu.

Erstelle eine Wertetabelle für $x\in [0;8]$ (auf Hunderter gerundete Werte).

Trage die Punkte in das Koordinatensystem ein und verbinde sie.

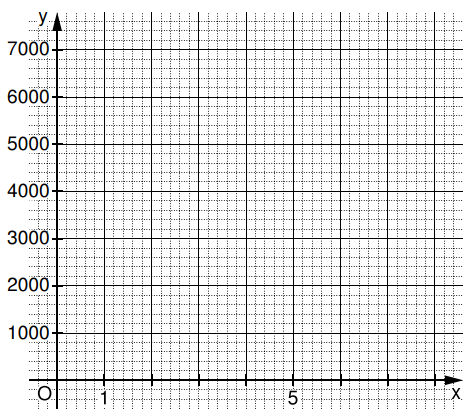
Berechne, welche Anzahl an Kegelrobben laut der Funktion $f$ am 1. Januar 2025 bekannt gegeben werden würde

Die Zeitrechnung beginnt am 1. Januar 2011.

Es ist nach der Zahl der Kegelrobben am 1. Januar 2025 gefragt.

Die verstrichene Zeit sind also 14 Jahre.

Berechne $f(14)=3300\cdot {\mathrm{1,1}}^{14}\approx 12500$ (auf Hunderter gerundet).

Am 1. Januar 2025 würde laut der Funktion $f$ eine Anzahl von gerundet

$12500$ Kegelrobben bekannt gegeben werden.

Ermittele rechnerisch das Datum, an dem laut der Funktion $f$ erstmals eine Anzahl von mehr als $20000$ Kegelrobben bekannt gegeben werden würde

Setze $20000=f(x)$ und löse nach $x$ auf.

$L=\{\mathrm{18,9}\}$

Zum 1. Januar 2011 müssen also rund $19$ Jahre addiert werden. Man ist dann im Jahr 2030.

Erstmals würde laut der Funktion $f$ am 1. Januar 2030 eine Anzahl von mehr als

$20000$ Kegelrobben bekannt gegeben werden.

Ergänze im Baumdiagramm die zugehörigen Anteile

Aus der Aufgabenstellung folgt:

Der Anteil der roten T-Shirts beträgt $p\%$.

$\Rightarrow$ Der Anteil der schwarzen T-Shirts beträgt $(100-p)\%$.

Von den roten T-Shirts wurden $24\%$ ohne Namensaufdruck geliefert.

$\Rightarrow$ Von den roten T-Shirts wurden $(100-24)\%=76\%$ mit Namensaufdruck geliefert.

Bei den schwarzen T-Shirts ist dieser Anteil (⁣$24\%$ ohne Namensaufdruck) doppelt so groß, d.h. er beträgt $2\cdot 24\%=48\%$.

$\Rightarrow$Der Anteil der schwarzen T-Shirts mit Namensaufdruck beträgt dann$(100-48)\%=52\%$.

Damit sind die im Baumdiagramm zugehörigen Anteile vollständig berechnet.

Zeige, dass der Anteil $p\%$ der roten T-Shirts $75\%$ beträgt

Gegeben ist:

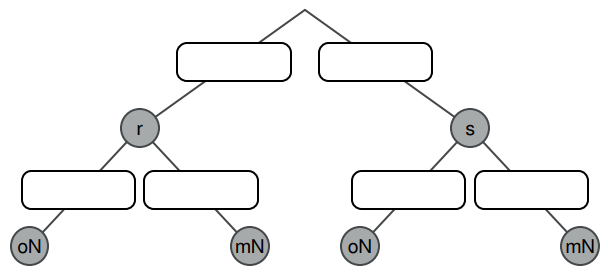
Der Anteil der roten T-Shirts ohne Namensaufdruck liegt bei $18\%$.

Folge dem ersten Pfad und stelle eine Gleichung auf:

${\displaystyle \frac{p}{100}}\cdot {\displaystyle \frac{24}{100}}={\displaystyle \frac{18}{100}}$ mit $p\in {ℝ}^{+}$

Löse die Gleichung nach $p$ auf:

$L=\{75\}$

Der Anteil $p\%$ der roten T-Shirts beträgt $75\%$.

Berechne die Wahrscheinlichkeit dafür, dass es ein T-Shirt mit Namensaufdruck ist

Folge den beiden Pfaden, die zu $mN$ führen.

$P(mN)=P(r,mN)+P(s,mN)={\displaystyle \frac{75}{100}}\cdot {\displaystyle \frac{76}{100}}+{\displaystyle \frac{100-75}{100}}\cdot {\displaystyle \frac{52}{100}}$$\Rightarrow P(mN)={\displaystyle \frac{5700+1300}{10000}}={\displaystyle \frac{7000}{10000}}=\mathrm{0,7}$

$L=\{70\%\}$

Die Wahrscheinlichkeit dafür, dass es ein T-Shirt mit Namensaufdruck ist, beträgt $70\%$.

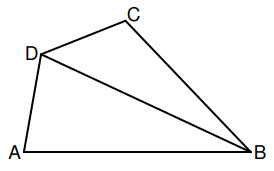
Zeichne das Viereck $ABCD$ sowie die Diagonale $\overline{BD}$

Zeichne die Strecke $|\overline{AB}|=10\text{ cm}$. Trage im Punkt $A$ den Winkel $\sphericalangle BAD={80}^{\circ }$ ab und im Punkt $B$ den Winkel $\sphericalangle DBA={25}^{\circ }$. Die freien Schenkel schneiden sich im Punkt $D$. Zeichne um $D$ einen Kreis mit dem Radius $r=4\text{ cm}$ und um $B$ einen Kreis mit dem Radius $r=8\text{ cm}$. Die beiden Kreise schneiden sich im Punkt $C$.

Verbinde die fehlenden Strecken.

Berechne die Länge der Strecke $\overline{BD}$

Verwende zur Berechnung der Länge der Strecke $\overline{BD}$ den Sinussatz.

${\displaystyle \frac{a}{\sin \left(\alpha \right)}}={\displaystyle \frac{b}{\sin \left(\beta \right)}}={\displaystyle \frac{c}{\sin \left(\gamma \right)}}$

$\Rightarrow {\displaystyle \frac{|\overline{BD}|}{\sin {80}^{\circ }}}={\displaystyle \frac{|\overline{AB}|}{\sin ({180}^{\circ }-{80}^{\circ }-{25}^{\circ })}}={\displaystyle \frac{10}{\sin {75}^{\circ }}}$

$\Rightarrow |\overline{BD}|={\displaystyle \frac{10}{\sin {75}^{\circ }}}\cdot \sin {80}^{\circ }\approx \mathrm{10,20}$

Die Länge der Strecke $\overline{BD}$ beträgt rund $\mathrm{10,20}\text{ cm}$.

Ergänze in der Zeichnung zur Aufgabenstellung die Strecke $\overline{EF}$

Beachte dabei:

Der Punkt $E$ liegt auf der Strecke $\overline{BD}$ mit $|\overline{BE}|=4\text{ cm}$. Der Punkt $F$ ist der Fußpunkt des Lotes von $E$ auf die Strecke $\overline{AB}$.

Berechne die Länge der Strecke $\overline{BF}$

Das Dreieck $BEF$ ist rechtwinklig.

Bekannt ist $|\overline{BE}|=4\text{ cm}$ und der Winkel $\sphericalangle DBA={25}^{\circ }$.

Es gilt:

$\cos \sphericalangle DBA={\displaystyle \frac{\overline{BF}}{\overline{BE}}}\Rightarrow \overline{BF}=\cos \sphericalangle DBA\cdot \overline{BE}=\cos {25}^{\circ }\cdot 4\approx \mathrm{3,63}$

Die Länge der Strecke $\overline{BF}$ beträgt rund $\mathrm{3,63}\text{ cm}$.

Zeichne die Strecke $\overline{FG}$ in die Zeichnung zur Aufgabenstellung ein.

Begründe, dass das Maß des Winkels $GFA$ gleich dem Maß des Winkels $DBA$ ist

Die Winkel $GFA$ und $DBA$ sind Stufenwinkel an den zueinander parallelen Geraden $BD$ und $FG$ und somit gleich groß.

Bestimme rechnerisch die Länge der Strecke $\overline{FG}$

Verwende den Strahlensatz (alle Einheiten in cm):

Es gilt:

${\displaystyle \frac{|\overline{FG}|}{\mathrm{10,20}}}={\displaystyle \frac{|\overline{AB}|-|\overline{BF}|}{|\overline{AB}|}}={\displaystyle \frac{10-\mathrm{3,63}}{10}}$

$\Rightarrow |\overline{FG}|={\displaystyle \frac{10-\mathrm{3,63}}{10}}\cdot \mathrm{10,20}\approx \mathrm{6,50}$

Die Länge der Strecke $\overline{FG}$ beträgt rund $\mathrm{6,50}\text{ cm}$.

Berechne das Maß des Winkels $DCB$

Verwende zur Berechnung den Kosinussatz.

Es gilt:

$\cos \sphericalangle DCB={\displaystyle \frac{|\overline{CD}{|}^2+|\overline{BC}{|}^2-|\overline{BD}{|}^2}{2\cdot |\overline{CD}|\cdot |\overline{BD}|}}={\displaystyle \frac{4^2+8^2-{\mathrm{10,20}}^2}{2\cdot 4\cdot 8}}$

$\Rightarrow \sphericalangle DCB={\cos }^{-1}\left({\displaystyle \frac{4^2+8^2-{\mathrm{10,20}}^2}{2\cdot 4\cdot 8}}\right)\approx {\mathrm{112,06}}^{\circ }$

Das Maß des Winkels $DCB$ beträgt rund ${\mathrm{112,06}}^{\circ }$.

Berechne den Flächeninhalt $A$ des Vierecks $ABCD$

Teile das Viereck in zwei Dreiecke $ABD$ und $BCD$.

$A_{\text{ABCD}}=A_{\text{ABD}}+A_{\text{BCD}}$

Die Berechnung des Flächeninhalts der beiden Dreiecke erfolgt mit zwei Seiten des Dreiecks und dem Sinus des eingeschlossenen Winkels.

Dann gilt z.B. $A_{\mathrm{\Delta }}=\frac{1}{2}\cdot a\cdot b\cdot \sin \gamma$ oder entsprechende Formeln.

Dann folgt:

$A_{\text{ABCD}}=A_{\text{ABD}}+A_{\text{BCD}}={\displaystyle \frac{1}{2}}\cdot |\overline{AB}|\cdot |\overline{BD}|\cdot \sin {25}^{\circ }+{\displaystyle \frac{1}{2}}\cdot |\overline{CD}|\cdot |\overline{BC}|\cdot \sin {\mathrm{112,06}}^{\circ }$

$A_{\text{ABCD}}=({\displaystyle \frac{1}{2}}\cdot 10\cdot \mathrm{10,20}\cdot \sin {25}^{\circ }+{\displaystyle \frac{1}{2}}\cdot 4\cdot 8\cdot \sin {\mathrm{112,06}}^{\circ })\approx \mathrm{36,38}$

Der Flächeninhalt $A$ des Vierecks $ABCD$ beträgt rund $\mathrm{36,38}{\text{ cm}}^2$.

Berechne den Radius $r$ dieses Kreissektors

Bekannt ist aus Aufgabe d) $\sphericalangle DCB={\mathrm{112,06}}^{\circ }$ und der Flächeninhalt $A$ des Vierecks $ABCD$ beträgt rund $\mathrm{36,38}{\text{ cm}}^2$.

Weiterhin gilt:

Der Flächeninhalt des Kreissektors mit dem Mittelpunkt $C$ und dem Mittelpunktswinkel $DCB$ beträgt $33\%$ des Flächeninhalts des Vierecks $ABCD$.

Berechne $33\%$ des Flächeninhalts des Vierecks $ABCD$

$\Rightarrow A_{\text{Kreissektor}}=\mathrm{0,33}\cdot \mathrm{36,38}{\text{ cm}}^2$

Benutze die Formel für den Flächeninhalt eines Kreissektors allgemein

Für den Flächeninhalt eines Kreissektors gilt allgemein:

$A_{\text{Kreissektor}}={\displaystyle \frac{\alpha }{{360}^{\circ }}}\cdot \pi \cdot r^2$

Erstelle eine Gleichung und löse nach $r$ auf

Mit dem Mittelpunktswinkel $\sphericalangle DCB={\mathrm{112,06}}^{\circ }$ folgt dann:

${\displaystyle \frac{{\mathrm{112,06}}^{\circ }}{{360}^{\circ }}}\cdot \pi \cdot r^2=\mathrm{0,33}\cdot \mathrm{36,38}$

Löse nach $r$ auf. (Der Radius $r$ hat die Einheit cm.)

Der Radius $r$ des Kreissektors beträgt rund $\mathrm{3,50}\text{ cm}$.

Ergänze den Kreissektor in der Zeichnung zur Aufgabenstellung

Zeichne um den Punkt $C$ einen Kreisbogen mit dem Radius $\mathrm{3,50}\text{ cm}$.

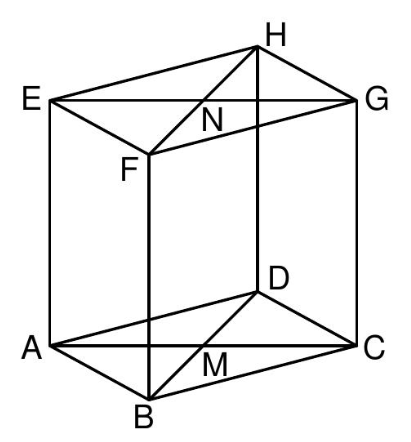
Zeichne das Schrägbild des Prismas $ABCDEFGH$ mit den Strecken $\overline{\mathrm{MN}}$ und $\overline{\mathrm{AN}}$

Zeichne die Strecke $\overline{AC}$ und markiere die Mitte dieser Strecke $M$. Trage im Punkt $M$ einen Winkel von $\omega ={45}^{\circ }$ an. Wegen $q=\frac{1}{2}$ beträgt die Länge der Diagonalen $\overline{BD}$ nur $5\text{ cm}$. Zeichne in den Punkten $A,B,C$, $D$ und $M$ jeweils eine Senkrechte mit einer Länge von $8\text{ cm}$.

Verbinde die Punkte $A,B,C$ und $D$ ebenso die Punkte $E,F,G$ und $H$. Verbinde weiterhin die Punkte $E$ mit $G$ und $F$ mit $H$. Der Schnittpunkt der Strecken $\overline{EG}$ und $\overline{FH}$ ist der Punkt $N$. Verbinde $A$ mit $N$.

Berechne die Länge der Strecke $\overline{\mathrm{AN}}$

Betrachte das rechtwinklige Dreieck $AMN$:

Verwende den Satz des Pythagoras:

$|\overline{\mathrm{AN}}|=\sqrt{(\mathrm{0,5}\cdot 10{)}^2+8^2}\approx \mathrm{9,43}$

Die Länge der Strecke $\overline{\mathrm{AN}}$ beträgt etwa $\mathrm{9,43}\text{ cm}$.

Berechne das Maß des Winkels CAN

Verwende zur Berechnung den Tangens:

$\tan \sphericalangle CAN={\displaystyle \frac{|\overline{\mathrm{MN}}|}{|\overline{\mathrm{AM}}|}}={\displaystyle \frac{8}{5}}\Rightarrow \sphericalangle CAN={\tan }^{-1}\left({\displaystyle \frac{8}{5}}\right)\approx {\mathrm{57,99}}^{\circ }$

Das Maß des Winkels $CAN$ beträgt rund ${\mathrm{57,99}}^{\circ }$.

Zeichnen Sie die Pyramide $P_1{Q}_1{R}_1{S}_{1}N$ und den Punkt $L_1$ für $x=4$ in das Schrägbild zu Aufgabe a) ein

Gib an, für welche Belegungen von $x$ es Pyramiden $P_n{Q}_n{R}_n{S}_{n}N$ gibt

Die Länge der Strecke $\overline{\mathrm{AN}}$ beträgt etwa $\mathrm{9,43}\text{ cm}$.

Deshalb gibt Pyramiden $P_n{Q}_n{R}_n{S}_{n}N$, wenn gilt: $0\le x<\mathrm{9,43}$.

Zeige, dass für den Flächeninhalt der Grundflächen $P_n{Q}_n{R}_n{S}_n$ der Pyramiden $P_n{Q}_n{R}_n{S}_{n}N$ in Abhängigkeit von $x$ gilt: $A(x)=(50-\mathrm{2,65}x){\mathrm{cm}}^2$

Für die Fläche des Drachenvierecks gilt:

$A_{\text{Drache}}={\displaystyle \frac{1}{2}}\cdot e\cdot f={\displaystyle \frac{1}{2}}\cdot (|\overline{{\mathrm{P}}_{\mathrm{n}}{\mathrm{L}}_{\mathrm{n}}}|+|\overline{{\mathrm{L}}_{\mathrm{n}}{\mathrm{R}}_{\mathrm{n}}}|)\cdot |\overline{{\mathrm{Q}}_{\mathrm{n}}{\mathrm{S}}_{\mathrm{n}}}|$

Unbekannt in der Flächengleichung ist $|\overline{{\mathrm{P}}_{\mathrm{n}}{\mathrm{L}}_{\mathrm{n}}}|$.

Betrachte das Dreieck $ANM$ und wende den Strahlensatz an.

Dann gilt:

${\displaystyle \frac{|\overline{{\mathrm{P}}_{\mathrm{n}}{\mathrm{L}}_{\mathrm{n}}}|}{|\overline{\mathrm{AM}}|}}={\displaystyle \frac{\mathrm{9,43}-x}{\mathrm{9,43}}}\Rightarrow |\overline{{\mathrm{P}}_{\mathrm{n}}{\mathrm{L}}_{\mathrm{n}}}|(x)=\mathrm{0,5}\cdot 10\cdot \left({\displaystyle \frac{\mathrm{9,43}-x}{\mathrm{9,43}}}\right)=(5-\mathrm{0,53}x)\text{ cm}$

Damit erhält man für die Fläche des Drachenvierecks:

$A_{\text{Drache}}={\displaystyle \frac{1}{2}}\cdot (|\overline{{\mathrm{P}}_{\mathrm{n}}{\mathrm{L}}_{\mathrm{n}}}|+|\overline{{\mathrm{L}}_{\mathrm{n}}{\mathrm{R}}_{\mathrm{n}}}|)\cdot |\overline{{\mathrm{Q}}_{\mathrm{n}}{\mathrm{S}}_{\mathrm{n}}}|$

$\Rightarrow A(x)={\displaystyle \frac{1}{2}}\cdot (5-\mathrm{0,53}x+\mathrm{0,5}\cdot 10)\cdot 10=5\cdot (10-\mathrm{0,53}x)=(50-\mathrm{2,65}x){\text{ cm}}^2$

Damit ist gezeigt, dass für den Flächeninhalt der Grundflächen $P_n{Q}_n{R}_n{S}_n$ der Pyramiden $P_n{Q}_n{R}_n{S}_{n}N$ in Abhängigkeit von $x$ gilt: $A(x)=(50-\mathrm{2,65}x){\mathrm{cm}}^2$.

Berechne den prozentualen Anteil des Volumens der Pyramide $P_1{Q}_1{R}_1{S}_{1}N$ am Volumen des Prismas $ABCDEFGH$

Berechne das Volumen des Prismas

$V_{\text{Prisma}}=G_{\text{Quadrat}}\cdot h$

Da vom Quadrat die Diagonalen gegeben sind, erhält man für den Flächeninhalt:

$G_{\text{Quadrat}}={\displaystyle \frac{1}{2}}\cdot 10\cdot 10{\text{ cm}}^2$

Die Prismahöhe beträgt $8\text{ cm}$.

$\Rightarrow V_{\text{Prisma}}={\displaystyle \frac{1}{2}}\cdot 10\cdot 10\cdot 8=400$

Das Volumen des Prismas beträgt $400{\text{ cm}}^3$.

Berechne das Volumen der Pyramide

Die Grundfläche der Pyramide in Abhängigkeit von $x$ wurde in Aufgabe c) berechnet: $A(x)=(50-\mathrm{2,65}x){\mathrm{cm}}^2$

Für die Pyramide $P_1{Q}_1{R}_1{S}_{1}N$ ist $x=4\Rightarrow A(4)=(50-\mathrm{2,65}\cdot 4){\mathrm{cm}}^2$.

$V_{P_1{Q}_1{R}_1{S}_{1}N}={\displaystyle \frac{1}{3}}\cdot A_{P_1{Q}_1{R}_1{S}_1}\cdot |\overline{L_{1}N|}={\displaystyle \frac{1}{3}}\cdot (50-\mathrm{2,65}\cdot 4)\cdot |\overline{L_{1}N|}$

Die Berechnung der Pyramidenhöhe $|\overline{L_{1}N|}$ erfolgt mit dem Strahlensatz.

Betrachte das Dreieck $ANM$.

Dann gilt:

${\displaystyle \frac{|\overline{{\mathrm{L}}_1\mathrm{N}}|}{8}}={\displaystyle \frac{\mathrm{9,43}-4}{\mathrm{9,43}}}\Rightarrow |\overline{{\mathrm{L}}_1\mathrm{N}}|=8\cdot \left({\displaystyle \frac{\mathrm{9,43}-4}{\mathrm{9,43}}}\right)\approx \mathrm{4,61}$

Die Pyramidenhöhe beträgt rund $\mathrm{4,61}\text{ cm}$.

Für das Pyramidenvolumen folgt dann:

$V_{P_1{Q}_1{R}_1{S}_{1}N}={\displaystyle \frac{1}{3}}\cdot (50-\mathrm{2,65}\cdot 4)\cdot \mathrm{4,61}\approx \mathrm{60,54}$

Das Volumen der Pyramide $P_1{Q}_1{R}_1{S}_{1}N$ beträgt rund $\mathrm{60,54}{\text{ cm}}^3$.

Berechne den prozentualen Anteil

Für den prozentualen Anteil erhält man:

${\displaystyle \frac{V_{P_1{Q}_1{R}_1{S}_{1}N}}{V_{\text{Prisma}}}}\cdot 100\%={\displaystyle \frac{\mathrm{60,54}}{400}}\cdot 100\%\approx \mathrm{15,14}\%$

Der prozentuale Anteil des Volumens der Pyramide $P_1{Q}_1{R}_1{S}_{1}N$ am Volumen des Prismas $ABCDEFGH$ beträgt rund $\mathrm{15,14}\%$.

Bestimme dieses Winkelmaß

Es gilt:

$\sphericalangle R_0{P}_{0}N=\sphericalangle N{R}_0{P}_0=\sphericalangle CAN={\mathrm{57,99}}^{\circ }$

Das Maß des Winkels $N{R}_0{P}_0$ beträgt ${\mathrm{57,99}}^{\circ }$.