Teil B - lernen mit Serlo!

Aufgabe B1

Gegeben ist die Funktion $f$ mit der Gleichung $y =-0{,}75\cdot \log_2 (x+1)+3 \;\;(x,y \in \mathbb{R})$ .

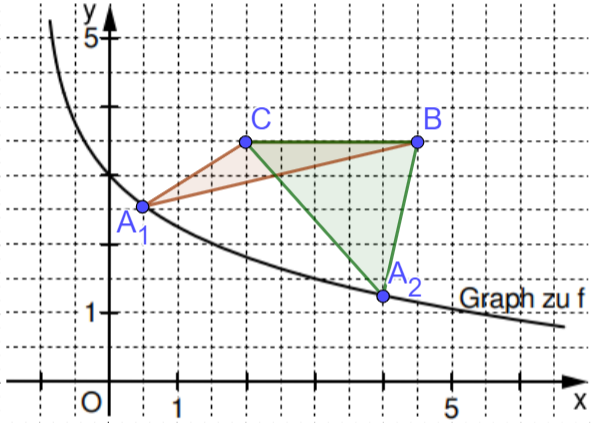
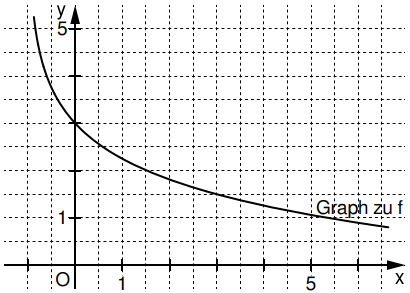
Im Koordinatensystem ist der Graph der Funktion $f$ bereits eingezeichnet.

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Punkte $A_n(x|-0{,}75\cdot \log_2 (x+1)+3)$ auf dem Graphen zu $f$ bilden zusammen mit den

Punkten $B (4,5 ∣ 3,5)$ und $C (2 ∣ 3,5)$ Dreiecke $A_{n} B C$ .

Ergänzen Sie im Koordinatensystem in der Zeichnung zur Aufgabenstellung die Dreiecke $A_{1} B C$ für $x = 0,5$ und $A_{2} B C$ für $x = 4$ .

Ermitteln Sie sodann rechnerisch, für welche Belegungen von $x$ es Dreiecke $A_{n} B C$

gibt. (4,5 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreieck

Gegeben sind $A_n(x|-0{,}75\cdot \log_2 (x+1)+3)$ und die Punkte $B (4,5 ∣ 3,5)$ und $C (2 ∣ 3,5)$ .

Beim Dreieck $A_{1} B C$ ist $x = 0,5$ .

$A_1(0{,}5|f(0{,}5))$ liegt auf dem Graphen von $f$ .

Zeichne $A_{1}, B$ und $C$ in das Koordinatensystem ein und verbinde die Punkte zu einem Dreieck (braunes Dreieck).

Beim Dreieck $A_{2} B C$ ist $x = 4$ .

$A_{2} (4 ∣ f (4))$ liegt auf dem Graphen von $f$ .

Zeichne $A_{2}$ in das Koordinatensystem ein und verbinde die Punkte $A_{2}, B$ und $C$ zu einem Dreieck (grünes Dreieck).

Die y-Koordinate von $A_{n}$ muss kleiner als $3,5$ sein, damit man Dreiecke $A_{n} B C$ zeichnen kann.

Löse die Gleichung $3{,}5=-0{,}75\cdot \log_2 (x+1)+3$ für $x \in \mathbb{R}$ :

$\Rightarrow\; L=\{-0{,}37\}$

Für $x > - 0,37$ ist $f (x) < 3,5$ . Folglich erhält man dann Dreiecke $A_{n} B C$ .