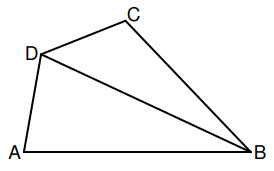
Zeichne das Viereck $ABCD$ sowie die Diagonale $\overline{BD}$

Zeichne die Strecke $|\overline{AB}|=10\text{ cm}$. Trage im Punkt $A$ den Winkel $\sphericalangle BAD={80}^{\circ }$ ab und im Punkt $B$ den Winkel $\sphericalangle DBA={25}^{\circ }$. Die freien Schenkel schneiden sich im Punkt $D$. Zeichne um $D$ einen Kreis mit dem Radius $r=4\text{ cm}$ und um $B$ einen Kreis mit dem Radius $r=8\text{ cm}$. Die beiden Kreise schneiden sich im Punkt $C$.

Verbinde die fehlenden Strecken.

Berechne die Länge der Strecke $\overline{BD}$

Verwende zur Berechnung der Länge der Strecke $\overline{BD}$ den Sinussatz.

${\displaystyle \frac{a}{\sin \left(\alpha \right)}}={\displaystyle \frac{b}{\sin \left(\beta \right)}}={\displaystyle \frac{c}{\sin \left(\gamma \right)}}$

$\Rightarrow {\displaystyle \frac{|\overline{BD}|}{\sin {80}^{\circ }}}={\displaystyle \frac{|\overline{AB}|}{\sin ({180}^{\circ }-{80}^{\circ }-{25}^{\circ })}}={\displaystyle \frac{10}{\sin {75}^{\circ }}}$

$\Rightarrow |\overline{BD}|={\displaystyle \frac{10}{\sin {75}^{\circ }}}\cdot \sin {80}^{\circ }\approx \mathrm{10,20}$

Die Länge der Strecke $\overline{BD}$ beträgt rund $\mathrm{10,20}\text{ cm}$.

Ergänze in der Zeichnung zur Aufgabenstellung die Strecke $\overline{EF}$

Beachte dabei:

Der Punkt $E$ liegt auf der Strecke $\overline{BD}$ mit $|\overline{BE}|=4\text{ cm}$. Der Punkt $F$ ist der Fußpunkt des Lotes von $E$ auf die Strecke $\overline{AB}$.

Berechne die Länge der Strecke $\overline{BF}$

Das Dreieck $BEF$ ist rechtwinklig.

Bekannt ist $|\overline{BE}|=4\text{ cm}$ und der Winkel $\sphericalangle DBA={25}^{\circ }$.

Es gilt:

$\cos \sphericalangle DBA={\displaystyle \frac{\overline{BF}}{\overline{BE}}}\Rightarrow \overline{BF}=\cos \sphericalangle DBA\cdot \overline{BE}=\cos {25}^{\circ }\cdot 4\approx \mathrm{3,63}$

Die Länge der Strecke $\overline{BF}$ beträgt rund $\mathrm{3,63}\text{ cm}$.

Zeichne die Strecke $\overline{FG}$ in die Zeichnung zur Aufgabenstellung ein.

Begründe, dass das Maß des Winkels $GFA$ gleich dem Maß des Winkels $DBA$ ist

Die Winkel $GFA$ und $DBA$ sind Stufenwinkel an den zueinander parallelen Geraden $BD$ und $FG$ und somit gleich groß.

Bestimme rechnerisch die Länge der Strecke $\overline{FG}$

Verwende den Strahlensatz (alle Einheiten in cm):

Es gilt:

${\displaystyle \frac{|\overline{FG}|}{\mathrm{10,20}}}={\displaystyle \frac{|\overline{AB}|-|\overline{BF}|}{|\overline{AB}|}}={\displaystyle \frac{10-\mathrm{3,63}}{10}}$

$\Rightarrow |\overline{FG}|={\displaystyle \frac{10-\mathrm{3,63}}{10}}\cdot \mathrm{10,20}\approx \mathrm{6,50}$

Die Länge der Strecke $\overline{FG}$ beträgt rund $\mathrm{6,50}\text{ cm}$.

Berechne das Maß des Winkels $DCB$

Verwende zur Berechnung den Kosinussatz.

Es gilt:

$\cos \sphericalangle DCB={\displaystyle \frac{|\overline{CD}{|}^2+|\overline{BC}{|}^2-|\overline{BD}{|}^2}{2\cdot |\overline{CD}|\cdot |\overline{BD}|}}={\displaystyle \frac{4^2+8^2-{\mathrm{10,20}}^2}{2\cdot 4\cdot 8}}$

$\Rightarrow \sphericalangle DCB={\cos }^{-1}\left({\displaystyle \frac{4^2+8^2-{\mathrm{10,20}}^2}{2\cdot 4\cdot 8}}\right)\approx {\mathrm{112,06}}^{\circ }$

Das Maß des Winkels $DCB$ beträgt rund ${\mathrm{112,06}}^{\circ }$.

Berechne den Flächeninhalt $A$ des Vierecks $ABCD$

Teile das Viereck in zwei Dreiecke $ABD$ und $BCD$.

$A_{\text{ABCD}}=A_{\text{ABD}}+A_{\text{BCD}}$

Die Berechnung des Flächeninhalts der beiden Dreiecke erfolgt mit zwei Seiten des Dreiecks und dem Sinus des eingeschlossenen Winkels.

Dann gilt z.B. $A_{\mathrm{\Delta }}=\frac{1}{2}\cdot a\cdot b\cdot \sin \gamma$ oder entsprechende Formeln.

Dann folgt:

$A_{\text{ABCD}}=A_{\text{ABD}}+A_{\text{BCD}}={\displaystyle \frac{1}{2}}\cdot |\overline{AB}|\cdot |\overline{BD}|\cdot \sin {25}^{\circ }+{\displaystyle \frac{1}{2}}\cdot |\overline{CD}|\cdot |\overline{BC}|\cdot \sin {\mathrm{112,06}}^{\circ }$

$A_{\text{ABCD}}=({\displaystyle \frac{1}{2}}\cdot 10\cdot \mathrm{10,20}\cdot \sin {25}^{\circ }+{\displaystyle \frac{1}{2}}\cdot 4\cdot 8\cdot \sin {\mathrm{112,06}}^{\circ })\approx \mathrm{36,38}$

Der Flächeninhalt $A$ des Vierecks $ABCD$ beträgt rund $\mathrm{36,38}{\text{ cm}}^2$.

Berechne den Radius $r$ dieses Kreissektors

Bekannt ist aus Aufgabe d) $\sphericalangle DCB={\mathrm{112,06}}^{\circ }$ und der Flächeninhalt $A$ des Vierecks $ABCD$ beträgt rund $\mathrm{36,38}{\text{ cm}}^2$.

Weiterhin gilt:

Der Flächeninhalt des Kreissektors mit dem Mittelpunkt $C$ und dem Mittelpunktswinkel $DCB$ beträgt $33\%$ des Flächeninhalts des Vierecks $ABCD$.

Berechne $33\%$ des Flächeninhalts des Vierecks $ABCD$

$\Rightarrow A_{\text{Kreissektor}}=\mathrm{0,33}\cdot \mathrm{36,38}{\text{ cm}}^2$

Benutze die Formel für den Flächeninhalt eines Kreissektors allgemein

Für den Flächeninhalt eines Kreissektors gilt allgemein:

$A_{\text{Kreissektor}}={\displaystyle \frac{\alpha }{{360}^{\circ }}}\cdot \pi \cdot r^2$

Erstelle eine Gleichung und löse nach $r$ auf

Mit dem Mittelpunktswinkel $\sphericalangle DCB={\mathrm{112,06}}^{\circ }$ folgt dann:

${\displaystyle \frac{{\mathrm{112,06}}^{\circ }}{{360}^{\circ }}}\cdot \pi \cdot r^2=\mathrm{0,33}\cdot \mathrm{36,38}$

Löse nach $r$ auf. (Der Radius $r$ hat die Einheit cm.)

Der Radius $r$ des Kreissektors beträgt rund $\mathrm{3,50}\text{ cm}$.

Ergänze den Kreissektor in der Zeichnung zur Aufgabenstellung

Zeichne um den Punkt $C$ einen Kreisbogen mit dem Radius $\mathrm{3,50}\text{ cm}$.