Heft 2 - B2
🎓 Prüfungsbereich für Schleswig-Holstein
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Aufgaben und Lösungen des Mathe ESA 2024 Prüfungsteil 2 Aufgabe 2.
Ein Taschenrechner ist in diesem Prüfungsteil erlaubt.
- 1
Die Kieler Woche ist ein großes Volksfest, bei dem Segelwettbewerbe stattfinden.
Die Abbildung zeigt die Besucherzahlen der Kieler Woche in verschiedenen Jahren.
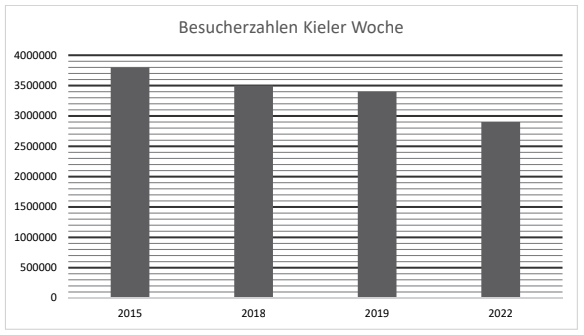
Gib die Anzahl der Besucher der Kieler Woche im Jahr 2019 an. /1P.
Merle sagt: „2022 hatte die Kieler Woche ca. weniger Besucher als in 2015.“
Zeige, dass Merle recht hat. /2P.
- 2
Bei einer Segelwettfahrt der 470er-Klasse muss der Flächeninhalt des dargestellten Segels betragen.
vereinfachte Darstellung
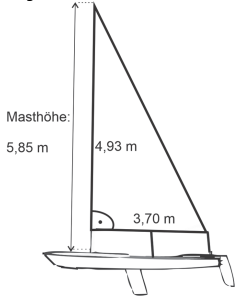
Überprüfe, ob das abgebildete Boot diese Bedingung erfüllt. /3P.
Bei der Wettfahrt müssen die Segler den abgebildeten Kurs einmal umfahren.
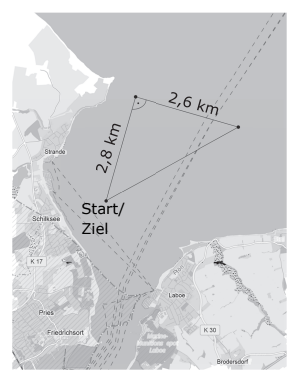
Bestimme die ungefähre Länge der zu segelnden Gesamtstrecke in Kilometern. /3P.
- 3
Während der Kieler Woche werden Fahrzeuge auf der abgebildeten Parkplatzfläche abgestellt.
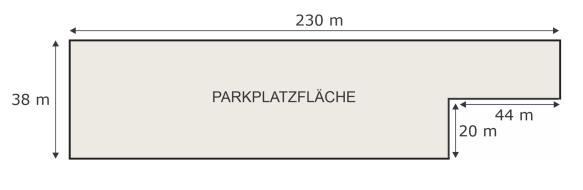
Bestimme den Flächeninhalt der gesamten Parkplatzfläche in Quadratmetern. /3P.
- 4
WAHLTEIL zu B2
Du musst einen der beiden Wahlteile bearbeiten.

Während der Kieler Woche kann man Lose kaufen. In der Lostrommel liegen Lose. Die Tabelle zeigt die jeweilige Anzahl der Arten von Losen.
Maria sagt: „Die Wahrscheinlichkeit, dass beim ersten Ziehen ein mittlerer Gewinn gezogen wird, beträgt über .“
Zeige, dass Maria nicht recht hat. /1 P.
Die ersten gezogenen Lose waren alles Nieten.
Karl behauptet: „Die Wahrscheinlichkeit, als nächstes einen Hauptgewinn zu ziehen, ist größer als am Anfang.“
Entscheide und begründe, ob Karl recht hat. /2P.
Am Ende sind noch folgende Lose in der Lostrommel.
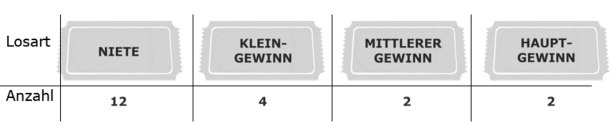
Gib an, wie viele Lose nacheinander höchstens gezogen werden
müssten, um sicher einen Gewinn zu ziehen. /1 P.
Als Ersatz für eine Lostrommel kann ein Glücksrad genutzt werden.
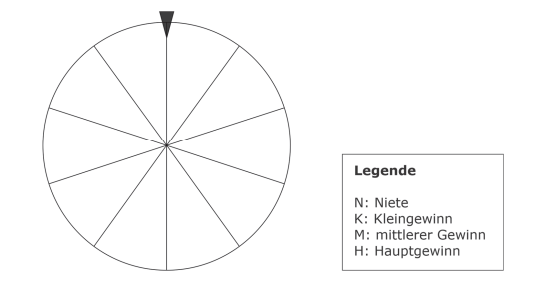
Die Wahrscheinlichkeiten aus 4c) sollen auf dieses Glücksrad übertragen
werden.
Beschrifte die Felder des Glückrades mit den Buchstaben N, K, M und H. /2P.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?