Teil B: Vektorielle Geometrie

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Gegeben sind das gerade Prisma $A B C D E F$ mit den Eckpunkten $C (0 | 0 | 0), D (6 | 0 | 5)$ , $E (0 | 8 | 5)$ und $F (0 | 0 | 5)$ sowie der Punkt $M (3 | 4 | 5)$ (vgl. Abbildung 1).
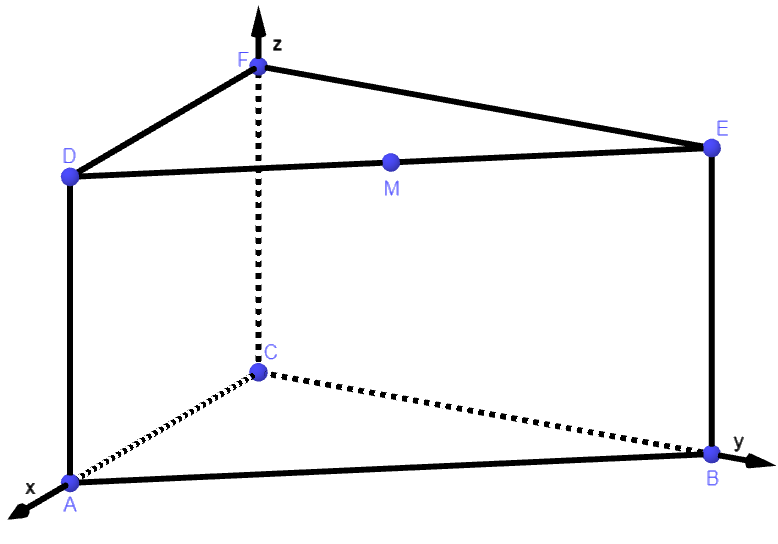
1. Geben Sie die Koordinaten des Punktes $A$ an. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatengeometrie im Raum
  Gib die Koordinaten des Punktes $A$ an
  Der Punkt $A$ liegt auf der x-Achse, senkrecht unter dem Punkt $D (6 | 0 | 5)$ .
  Demnach gilt: $A (6 | 0 | 0)$ .
  Die Koordinaten des Punktes $A$ sind $(6 | 0 | 0)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Punkt $A$ liegt auf der x-Achse, senkrecht unter dem Punkt $D (6 | 0 | 5)$ .
2. Berechnen Sie die Größe des Innenwinkels des Dreiecks $D E F$ bei $D$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
  Berechne die Größe des Innenwinkels des Dreiecks $D E F$ bei $D$
  Mit $α$ wird der Innenwinkel des Dreiecks $D E F$ bei $D$ bezeichnet.
  Dann gilt:
  $\begin{aligned} \cos (α) = \frac{\vec{D E} \circ \vec{D F}}{| \vec{D E} | \cdot | \vec{D F} |} \end{aligned}$
  Berechne die Vektoren und ihre Beträge:
  $\vec{D E} = \vec{O E} - \vec{O D} = (\begin{array}{c} 0 \\ 8 \\ 5 \end{array}) - (\begin{array}{c} 6 \\ 0 \\ 5 \end{array}) = (\begin{array}{c} - 6 \\ 8 \\ 0 \end{array})$
  $| \vec{D E} | = \sqrt{(- 6)^{2} + 8^{2} + 0} = \sqrt{100} = 10$
  $\vec{D F} = \vec{O F} - \vec{O D} = (\begin{array}{c} 0 \\ 0 \\ 5 \end{array}) - (\begin{array}{c} 6 \\ 0 \\ 5 \end{array}) = (\begin{array}{c} - 6 \\ 0 \\ 0 \end{array})$
  $| \vec{D F} | = 6$
  Setze die berechneten Größen in den Kosinus ein:
  $\cos (α) = \frac{(\begin{array}{c} - 6 \\ 8 \\ 0 \end{array}) \circ (\begin{array}{c} - 6 \\ 0 \\ 0 \end{array})}{10 \cdot 6} = \frac{36}{60} = 0,6$
  $\Rightarrow α = \cos^{- 1} (0,6) \approx {53,13}^{\circ}$
  Die Größe des Innenwinkels des Dreiecks $D E F$ bei $D$ beträgt rund ${53,13}^{\circ}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Vektoren $\vec{D E}$ , $\vec{D F}$ und ihre Beträge.
  Setze in $\begin{aligned} \cos (α) = \frac{\vec{D E} \circ \vec{D F}}{| \vec{D E} | \cdot | \vec{D F} |} \end{aligned}$ ein.
3. Berechnen Sie den Inhalt der Oberfläche des Prismas. (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prisma
  Berechne den Inhalt der Oberfläche des Prismas
  Für die Oberflächenberechnung werden verschiedene Vektoren und ihre Beträge benötigt.
  Aus Aufgabe a) folgt:
  $\vec{D E} = (\begin{array}{c} - 6 \\ 8 \\ 0 \end{array})$ , $| \vec{D E} | = 10$
  $\vec{D F} = (\begin{array}{c} - 6 \\ 0 \\ 0 \end{array})$ , $| \vec{D F} | = 6$
  Berechne weiter:
  $\begin{array}{l} \vec{F E} = \vec{O E} - \vec{O F} = (\begin{array}{c} 0 \\ 8 \\ 5 \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 5 \end{array}) = (\begin{array}{c} 0 \\ 8 \\ 0 \end{array}) \\ | \vec{F E} | = 8 \end{array}$
  Die Höhe des Prismas ist $h = 5$ .
  Dann folgt für den Oberflächeninhalt des Prismas:
  $O_{Prisma} = | \vec{D F} | \cdot h + | \vec{E F} | \cdot h + | \vec{D E} | \cdot h + 2 \cdot \frac{1}{2} \cdot | \vec{D F} | \cdot | \vec{E F} |$
  $O_{Prisma} = (6 + 8 + 10) \cdot 5 + 2 \cdot \frac{1}{2} \cdot 6 \cdot 8 = 168$
  Der Inhalt der Oberfläche des Prismas beträgt $168 FE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Vektor $\vec{F E}$ und seinen Betrag.
  Die Höhe des Prismas ist die z-Koordinate eines in der Deckfläche liegenden Punktes.
  $O_{Prisma} = | \vec{D F} | \cdot h + | \vec{E F} | \cdot h + | \vec{D E} | \cdot h + 2 \cdot \frac{1}{2} \cdot | \vec{D F} | \cdot | \vec{E F} |$
4. Begründen Sie, dass die Punkte $D, E$ und $F$ auf einem Kreis mit dem Mittelpunkt $M$ liegen. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Einführung zum Kreis
  Begründe, dass die Punkte $D, E$ und $F$ auf einem Kreis mit dem Mittelpunkt $M$ liegen
  Berechne die Vektoren $\vec{D M}, \vec{F M}$ und $\vec{E M}$ , sowie ihre Beträge.
  $\vec{D M} = \vec{O M} - \vec{O D} = (\begin{array}{c} 3 \\ 4 \\ 5 \end{array}) - (\begin{array}{c} 6 \\ 0 \\ 5 \end{array}) = (\begin{array}{c} - 3 \\ 4 \\ 0 \end{array})$
  $| \vec{D M} | = \sqrt{(- 3)^{2} + 4^{2} + 0} = \sqrt{25} = 5$
  $\vec{F M} = \vec{O M} - \vec{O F} = (\begin{array}{c} 3 \\ 4 \\ 5 \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 5 \end{array}) = (\begin{array}{c} 3 \\ 4 \\ 0 \end{array})$
  $| \vec{F M} | = \sqrt{3^{2} + 4^{2} + 0} = \sqrt{25} = 5$
  $\vec{E M} = \vec{O M} - \vec{O E} = (\begin{array}{c} 3 \\ 4 \\ 5 \end{array}) - (\begin{array}{c} 0 \\ 8 \\ 5 \end{array}) = (\begin{array}{c} 3 \\ - 4 \\ 0 \end{array})$
  $| \vec{E M} | = \sqrt{3^{2} + (- 4)^{2} + 0} = \sqrt{25} = 5$
  Es gilt: $| \vec{D M} | = | \vec{F M} | = | \vec{E M} | = 5$
  Alle Punkte liegen zusammen mit $M$ in einer Ebene und haben den gleichen Abstand $5$ vom Punkt $M$ und liegen deshalb auf einem Kreis um $M$ mit dem Radius $5$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Vektoren $\vec{D M}, \vec{F M}$ und $\vec{E M}$ , sowie ihre Beträge.
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
In Aufgabe 1 sind das gerade Prisma $A B C D E F$ mit den Eckpunkten $C (0 | 0 | 0), D (6 | 0 | 5)$ , $E (0 | 8 | 5)$ und $F (0 | 0 | 5)$ sowie der Punkt $M (3 | 4 | 5)$ gegeben.
Die Ebene $W$ enthält die Punkte $M, F$ und $S (7,5 | 0 | 0)$ (vgl. Abbildung 2).
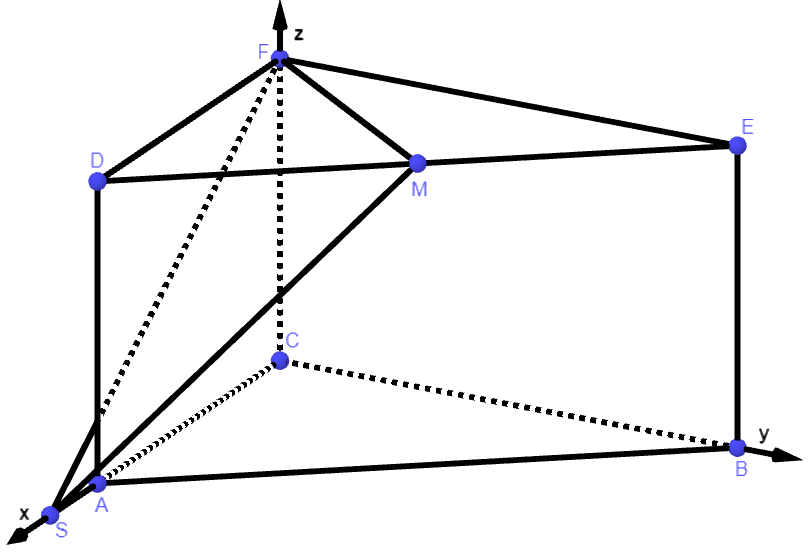
Abbildung 2
1. Begründen Sie, dass
  $\vec{x} = (\begin{array}{l} 0 \\ 0 \\ 5 \end{array}) + m \cdot (\begin{array}{l} 3 \\ 4 \\ 0 \end{array}) + n \cdot (\begin{array}{c} 7,5 \\ 0 \\ - 5 \end{array}), m \in ℝ, n \in ℝ,$
  eine Gleichung von $W$ in Parameterform ist. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene aus drei Punkten
  Begründe, dass die gegebene Ebenengleichung eine Gleichung von $W$ in Parameterform ist
  Gegeben ist: $\vec{x} = (\begin{array}{l} 0 \\ 0 \\ 5 \end{array}) + m \cdot (\begin{array}{l} 3 \\ 4 \\ 0 \end{array}) + n \cdot (\begin{array}{c} 7,5 \\ 0 \\ - 5 \end{array})$
  Die Ebene $W$ enthält die Punkte $M (3 | 4 | 5), F (0 | 0 | 5)$ und $S (7,5 | 0 | 0)$ .
  Wegen $(\begin{array}{l} 0 \\ 0 \\ 5 \end{array}) + m \cdot (\begin{array}{l} 3 \\ 4 \\ 0 \end{array}) + n \cdot (\begin{array}{c} 7,5 \\ 0 \\ - 5 \end{array}) = \vec{O F} + m \cdot \vec{F M} + n \cdot \vec{F S}$ ist die angegebene Gleichung eine Parametergleichung der Ebene $W$ .
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Stelle die Ebenengleichung mit den Punkten $F, M$ und $S$ auf und vergleiche sie mit der angegebenen Ebenengleichung.
2. Im Folgenden sind zwei Schritte der Lösung einer Aufgabe angegeben, die im Zusammenhang mit den betrachteten geometrischen Objekten steht:
  (I) $P (6 | 0 | r) mit 0 \leq r \leq 5$
  (II) $| \begin{array}{lcc} 6 & = & 3 \cdot m + 7,5 \cdot n \\ 0 & = & 4 \cdot m \\ r & = & 5 - 5 \cdot n \end{array} |$ .
  Geben Sie eine passende Aufgabenstellung an. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung Punkt-Ebene (Inzidenz)
  Gib eine passende Aufgabenstellung an
  In (I) ist der Punkt $P$ gegeben. Er liegt für $0 \leq r \leq 5$ auf der Strecke $A D$ .
  Gleichung (II): Es wird geprüft, ob der Punkt $P$ in der Ebene $W$ aus Aufgabe a) liegt.
  Daraus ergibt sich die folgende Aufgabenstellung:
  Bestimmen Sie die Koordinaten des Punktes der Strecke $A D$ , der in der Ebene $W$ liegt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Was ist in (I) gegeben und was stellt die Gleichung in (II) dar?
3. Gegeben ist die Gerade $g$ durch die Gleichung
  $g : \vec{x} = (\begin{array}{c} - 1,5 \\ 8 \\ 10 \end{array}) + k \cdot (\begin{array}{c} 7,5 \\ 0 \\ - 5 \end{array}), k \in ℝ$
  Die Gerade $h$ verläuft durch die Punkte $S$ und $M$ und lässt sich beschreiben durch
  $h : \vec{x} = \vec{O S} + q \cdot \vec{S M} = (\begin{array}{c} 7,5 \\ 0 \\ 0 \end{array}) + q \cdot (\begin{array}{c} - 4,5 \\ 4 \\ 5 \end{array}), q \in ℝ$ .
  Untersuchen Sie rechnerisch, ob die Gerade $g$ und die Strecke $S M$ einen gemeinsamen Punkt besitzen. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineares Gleichungssystem
  Untersuche rechnerisch, ob die Gerade $g$ und die Strecke $S M$ einen gemeinsamen Punkt besitzen
  Setze $g = h$ :
  $(\begin{array}{c} - 1,5 \\ 8 \\ 10 \end{array}) + k \cdot (\begin{array}{c} 7,5 \\ 0 \\ - 5 \end{array}) = (\begin{array}{c} 7,5 \\ 0 \\ 0 \end{array}) + q \cdot (\begin{array}{c} - 4,5 \\ 4 \\ 5 \end{array})$
  $\Rightarrow (\begin{array}{c} - 1,5 \\ 8 \\ 10 \end{array}) - (\begin{array}{c} 7,5 \\ 0 \\ 0 \end{array}) = k \cdot (\begin{array}{c} - 7,5 \\ 0 \\ 5 \end{array}) + q \cdot (\begin{array}{c} - 4,5 \\ 4 \\ 5 \end{array})$
  $\Rightarrow (\begin{array}{c} - 9 \\ 8 \\ 10 \end{array}) = k \cdot (\begin{array}{c} - 7,5 \\ 0 \\ 5 \end{array}) + q \cdot (\begin{array}{c} - 4,5 \\ 4 \\ 5 \end{array})$
  Aus Gleichung $II$ folgt $8 = 4 \cdot q \Rightarrow q = 2$
  Mit $q = 2$ erhält man in Gleichung $III : 10 = 5 \cdot k + 2 \cdot 5 \Rightarrow k = 0$
  Eingesetz in Gleichung $I : - 9 = 0 \cdot (- 7,5) + 2 \cdot (- 4,5) ✓$
  Demnach sind $q = 2$ und $k = 0$ die Lösungen des Gleichungssystems.
  Wegen $2 \notin [0; 1]$ besitzen die Gerade $g$ und die Strecke $S M$ keinen gemeinsamen Punkt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze $g = h$ und löse das Gleichungssystem nach $k$ und $q$ auf.
  Wenn $0 \leq q \leq 1$ , dann haben die Gerade $g$ und die Strecke $S M$ einen gemeinsamen Punkt.
4. Anstelle des Punktes $S$ werden nun Punkte $S_{t} (t | 0 | 0)$ mit $t \geq 0$ auf der $x$ -Achse betrachtet.
  Bestimmen Sie denjenigen Wert von $t$ , für den das Dreieck $M F S$ im Punkt $M$ rechtwinklig ist. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Bestimme denjenigen Wert von $t$ , für den das Dreieck $M F S$ im Punkt $M$ rechtwinklig ist
  Berechne die Vektoren $\vec{M S_{t}}$ und $\vec{M F}$ .
  $\vec{M S_{t}} = \vec{O S_{t}} - \vec{O M} = (\begin{array}{c} t \\ 0 \\ 0 \end{array}) - (\begin{array}{c} 3 \\ 4 \\ 5 \end{array}) = (\begin{array}{c} t - 3 \\ - 4 \\ - 5 \end{array})$
  $\vec{M F} = \vec{O F} - \vec{O M} = (\begin{array}{c} 0 \\ 0 \\ 5 \end{array}) - (\begin{array}{c} 3 \\ 4 \\ 5 \end{array}) = (\begin{array}{c} - 3 \\ - 4 \\ 0 \end{array})$
  Für einen rechten Winkel muss das Skalarprodukt der beiden Vektoren gleich null sein.
  $\vec{M S_{t}} \circ \vec{M F} = 0 \Rightarrow (\begin{array}{c} t - 3 \\ - 4 \\ - 5 \end{array}) \circ (\begin{array}{c} - 3 \\ - 4 \\ 0 \end{array}) = - 3 \cdot t + 9 + 16 + 0 = 0 \Rightarrow t = \frac{25}{3}$
  Für $t = \frac{25}{3}$ ist das Dreieck $M F S$ im Punkt $M$ rechtwinklig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Vektoren $\vec{M S_{t}}$ und $\vec{M F}$ .
  Für einen rechten Winkel muss das Skalarprodukt der beiden Vektoren gleich null sein.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Teil B: Vektorielle Geometrie

Aufgabe 1

Gib die Koordinaten des Punktes A an

Hast du eine Frage oder Feedback?

Berechne die Größe des Innenwinkels des Dreiecks DEF bei D

Hast du eine Frage oder Feedback?

Berechne den Inhalt der Oberfläche des Prismas

Hast du eine Frage oder Feedback?

Begründe, dass die Punkte D,E und F auf einem Kreis mit dem Mittelpunkt M liegen

Hast du eine Frage oder Feedback?

Aufgabe 2

Begründe, dass die gegebene Ebenengleichung eine Gleichung von W in Parameterform ist

Hast du eine Frage oder Feedback?

Gib eine passende Aufgabenstellung an

Hast du eine Frage oder Feedback?

Untersuche rechnerisch, ob die Gerade g und die Strecke SM einen gemeinsamen Punkt besitzen

Hast du eine Frage oder Feedback?

Bestimme denjenigen Wert von t, für den das Dreieck MFS im Punkt M rechtwinklig ist

Hast du eine Frage oder Feedback?

Gib die Koordinaten des Punktes $A$ an

Berechne die Größe des Innenwinkels des Dreiecks $D E F$ bei $D$

Begründe, dass die Punkte $D, E$ und $F$ auf einem Kreis mit dem Mittelpunkt $M$ liegen

Begründe, dass die gegebene Ebenengleichung eine Gleichung von $W$ in Parameterform ist

Untersuche rechnerisch, ob die Gerade $g$ und die Strecke $S M$ einen gemeinsamen Punkt besitzen

Bestimme denjenigen Wert von $t$ , für den das Dreieck $M F S$ im Punkt $M$ rechtwinklig ist