Dieser Inhalt wurde gelöscht.

B4

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Ein Unternehmen stellt Olivenöl her und füllt es in Flaschen ab. Laut Aufdruck beträgt die Füllmenge jeder Flasche $600$ ml.
Die Flaschen werden in Kartons verpackt; jeder Karton enthält zwölf Flaschen. Ein Karton gilt als fehlerhaft, wenn mehr als eine Flasche weniger als $600$ ml Öl enthält.
Für jede Flasche beträgt die Wahrscheinlichkeit dafür, dass sie weniger als $600$ ml Öl enthält, $1,5 %$ .
1. Die Rechnung $0{,}985^{12} \approx 83{,}4 \%$ stellt im Sachzusammenhang die Lösung einer Aufgabe dar.
  Formulieren Sie eine passende Aufgabenstellung und erläutern Sie den Ansatz der Rechnung. (3 P)
  
  Formuliere eine passende Aufgabenstellung und erläutere den Ansatz der Rechnung
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimmen Sie die Wahrscheinlichkeit, dass sich unter $100$ Flaschen genau drei Flaschen mit weniger als $600$ ml Öl befinden. (2 P)
  
  Bestimme die Wahrscheinlichkeit, dass sich unter $100$ Flaschen genau drei Flaschen mit weniger als $600$ ml Öl befinden
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Es wird eine Flasche nach der anderen geöffnet und die Füllmenge überprüft.
  Ermitteln Sie die Wahrscheinlichkeit, dass die vierte geöffnete Flasche die erste überprüfte Flasche ist, die weniger als $600$ ml Öl enthält. (2 P)
  
  Ermittele die Wahrscheinlichkeit, dass die vierte geöffnete Flasche die erste überprüfte Flasche ist, die weniger als $600$ ml Öl enthält
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. An einen Supermarkt wird regelmäßig die gleiche Anzahl von Flaschen geliefert. Dabei enthalten im Mittel mehr als $780$ Flaschen mindestens $600$ ml Öl.
  Ermitteln Sie die Anzahl der Flaschen, die eine regelmäßige Lieferung mindestens umfasst. (3 P)
  
  Ermittele die Anzahl der Flaschen, die eine regelmäßige Lieferung mindestens umfasst
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Ein Supermarkt erhält eine Lieferung von $150$ Kartons.
  Bestimmen Sie die Wahrscheinlichkeit dafür, dass mehr als $3 %$ der Kartons fehlerhaft sind. (4 P)
  
  Bestimme die Wahrscheinlichkeit dafür, dass mehr als $3 %$ der Kartons fehlerhaft sind
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Die Füllmenge der Flaschen soll als normalverteilt mit einem Erwartungswert von $600,5$ ml und einer Standardabweichung von $0,23$ ml angenommen werden.
1. Eine Flasche wird zufällig ausgewählt.
  Ermitteln Sie für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:
  A: „Die Flasche enthält mehr als 601 ml Öl.“
  B: „Die Füllmenge der Flasche weicht höchstens um $0,5$ ml vom Erwartungswert ab.“
  (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  $A$ : „Die Flasche enthält mehr als $601 \mathrm{~ml}$ Öl.“
  $X$ : Füllmenge in $\mathrm{ml}$
  Normalverteilung mit $\mu=600{,}5\; \mathrm{ml}$ und $\sigma=0{,}23\; \mathrm{ml}$
  Gesucht ist: $P(X>601)=\text{normCdf}(601,\infty,600.5, 0.23)\approx0{,}0148558$
  Die Wahrscheinlichkeit, dass die Flasche mehr als $601\; \mathrm{ml}$ Öl enthält, beträgt rund $1,5 %$ .
  $B$ : „Die Füllmenge der Flasche weicht höchstens um $0{,}5\; \mathrm{ml}$ vom Erwartungswert ab.“
  Es ist $\mu-0{,}5=600$ und $\mu+0{,}5=601$
  Berechne: $P(600\leq X\leq601)=\text{normCdf}(600, 601, 600.5, 0.23)\approx0{,}9702884$
  Die Wahrscheinlichkeit, dass die Füllmenge der Flasche um höchstens $0{,}5\; \mathrm{ml}$ vom Erwartungswert abweicht, beträgt etwa $97 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  A: Berechne $P(X>601)=\text{normCdf}(601,\infty,600.5, 0.23)$ .
  B: Berechne $P(600\leq X\leq601)=\text{normCdf}(600, 601, 600.5, 0.23)$ .
2. Die Füllmenge einer Flasche ist nie negativ. Die Normalverteilung, die zur Beschreibung der Füllmenge der Flaschen verwendet wird, ist jedoch auch für negative reelle Zahlen definiert und nimmt dabei ausschließlich positive Werte an.
  Begründen Sie, dass die Verwendung der Normalverteilung dennoch sinnvoll ist.
  (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  Begründe, dass die Verwendung der Normalverteilung dennoch sinnvoll ist
  Die Wahrscheinlichkeit, die die verwendete Normalverteilung für negative Füllmengen liefert, ist so gering, dass sie im Sachzusammenhang vernachlässigt werden kann $\left(P_{600{,}5 ; 0{,}23}(X<0) \approx 0\right)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Zeige, dass $P_{600{,}5 ; 0{,}23}(X<0)$ ungefähr gleich null ist.
3. Das Unternehmen möchte die Wahrscheinlichkeit dafür, dass eine Flasche weniger als $600$ ml Öl enthält, verringern. Für die nötige Änderung der Maschine, die die Flaschen befüllt, gibt es zwei Vorschläge:
  Vorschlag 1： Die eingestellte Füllmenge von $600,5$ ml wird erhöht.
  Vorschlag 2: Die Genauigkeit, mit der die eingestellte Füllmenge von $600,5$ ml erreicht wird, wird erhöht.
  Die eingestellte Füllmenge entspricht stets dem Erwartungswert der Zufallsgröße.
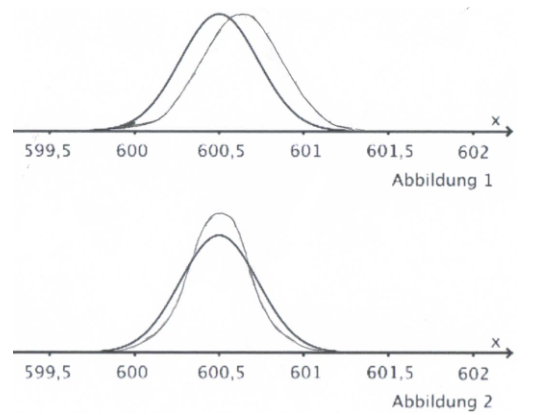
  Die Abbildungen 1 und 2 zeigen jeweils den Graphen der Dichtefunktion, die vor der Änderung der Maschine die Füllmenge der Flaschen beschreibt.
  Skizzieren Sie in Abbildung 1 den Graphen einer Dichtefunktion, die sich aus dem Vorschlag 1 ergeben könnte, und in Abbildung 2 den Graphen einer Dichtefunktion, die zum Vorschlag 2 passt.
  Begründen Sie für jeden Vorschlag mithilfe des skizzierten Graphen, dass damit das Ziel des Unternehmens erreicht wird. (6 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  Vorschlag 1:
  Der Erwartungswert der Verteilung muss größer werden, d.h. die Verteilung rutscht nach rechts. Die Form der Verteilung ändert sich nicht, d.h. die Genauigkeit der Abfüllung bleibt unverändert.
  Vorschlag 2:
  Hier muss der Erwartungswert beibehalten werden. Die Streuung um den Erwartungswert soll aber kleiner sein, d.h. der Graph wird etwas "schlanker". Dafür muss aber das Maximum größer werden, denn die Fläche unter dem Graphen muss weiterhin den Wert $1$ haben.
  Begründung für Vorschlag 1, damit das Ziel des Unternehmens erreicht wird
  Wie kann man am Graphen erkennen, wie wahrscheinlich es ist, dass die Flasche weniger als $600\; \mathrm{ml}$ Öl enthält?
  Man findet diese Wahrscheinlichkeit als Fläche zwischen dem Graphen und der x-Achse im Intervall von minus unendlich bis $600$ .
  Diese Fläche ist beim ursprünglichen Graphen größer als bei dem nach rechts verschobenen Graphen. In der Abbildung 1 ist die Fläche schwarz markiert, um die der ursprüngliche Graph in dem angegebenen Intervall größer ist.
  Mit anderen Worten: Vorschlag 1 führt durch die Verschiebung in positive 𝑥-Richtung zu einer Verkleinerung dieser Fläche.
  Der Vorschlag eignet sich dafür, dass die Firma ihr Ziel erreicht.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Vorschlag 1:
  Der Erwartungswert der Verteilung muss größer werden, d.h. die Verteilung rutscht nach rechts. Die Form der Verteilung ändert sich nicht.
  Vorschlag 2:
  Der Erwartungswert wird beibehalten. Die Streuung um den Erwartungswert soll aber kleiner sein, d.h. der Graph wird etwas "schlanker". Dafür muss aber das Maximum größer werden, denn die Fläche unter dem Graphen muss weiterhin den Wert $1$ haben.
  Die Wahrscheinlichkeit, dass die Flasche weniger als $600\; \mathrm{ml}$ Öl enthält, entspricht der Fläche zwischen dem Graphen und der x-Achse in Intervall $]-\infty; 600]$ . Vorschlag 1 führt durch die Verschiebung in positive 𝑥-Richtung zu einer Verkleinerung dieser Fläche.
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Ein Unternehmen stellt Olivenöl her und füllt es in Flaschen ab. Laut Aufdruck beträgt die Füllmenge jeder Flasche $600$ ml.
Die Flaschen werden in Kartons verpackt; jeder Karton enthält zwölf Flaschen. Ein Karton gilt als fehlerhaft, wenn mehr als eine Flasche weniger als $600$ ml Öl enthält.
Für jede Flasche beträgt die Wahrscheinlichkeit dafür, dass sie weniger als $600$ ml Öl enthält, $1,5 %$ .
1. Die Rechnung $0{,}985^{12} \approx 83{,}4 \%$ stellt im Sachzusammenhang die Lösung einer Aufgabe dar.
  Formulieren Sie eine passende Aufgabenstellung und erläutern Sie den Ansatz der Rechnung. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Gegenereignis
  Formuliere eine passende Aufgabenstellung und erläutere den Ansatz der Rechnung
  Aufgabenstellung: „Berechnen Sie die Wahrscheinlichkeit dafür, dass in einem Karton alle Flaschen mindestens $600$ ml Öl enthalten.“
  Die Wahrscheinlichkeit dafür, dass eine Flasche mindestens $600$ ml Öl enthält, beträgt $1 - 0,015 = 0,985$ , die Wahrscheinlichkeit dafür, dass alle Flaschen eines Kartons diese Eigenschaft haben, beträgt $0{,}985^{12}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte das Gegenereignis.
2. Bestimmen Sie die Wahrscheinlichkeit, dass sich unter $100$ Flaschen genau drei Flaschen mit weniger als $600$ ml Öl befinden. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Bestimme die Wahrscheinlichkeit, dass sich unter $100$ Flaschen genau drei Flaschen mit weniger als $600$ ml Öl befinden
  Es ist $n = 100, p = 0,015$ . $Y$ : Anzahl der Flaschen mit einer Füllmenge von weniger als $600$ ml.
  Berechne $P(Y=3)=\text{binomPdf}(100, 0.015{,}3)\approx0{,}126$ .
  Die Wahrscheinlichkeit, dass sich unter $100$ Flaschen genau drei Flaschen mit weniger als $600$ ml Öl befinden, beträgt rund $12{,}6\;\%$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es ist $n = 100, p = 0,015$ .
  $Y$ : Anzahl der Flaschen mit einer Füllmenge von weniger als $600$ ml.
  Berechne $P (Y = 3)$ .
3. Es wird eine Flasche nach der anderen geöffnet und die Füllmenge überprüft.
  Ermitteln Sie die Wahrscheinlichkeit, dass die vierte geöffnete Flasche die erste überprüfte Flasche ist, die weniger als $600$ ml Öl enthält. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Ermittele die Wahrscheinlichkeit, dass die vierte geöffnete Flasche die erste überprüfte Flasche ist, die weniger als $600$ ml Öl enthält
  Vor der ersten Flasche mit weniger als $600$ ml Inhalt müssen drei Flaschen mit mindestens $600$ ml Inhalt geöffnet worden sein. Daher ist die Wahrscheinlichkeit $0{,}985^{3} \cdot 0{,}015 \approx 0{,}014=1{,}4 \%$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Vor der ersten Flasche mit weniger als $600$ ml Inhalt müssen drei Flaschen mit mindestens $600$ ml Inhalt geöffnet worden sein.
  Was folgt dann für die Wahrscheinlichkeit?
4. An einen Supermarkt wird regelmäßig die gleiche Anzahl von Flaschen geliefert. Dabei enthalten im Mittel mehr als $780$ Flaschen mindestens $600$ ml Öl.
  Ermitteln Sie die Anzahl der Flaschen, die eine regelmäßige Lieferung mindestens umfasst. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
  Ermittele die Anzahl der Flaschen, die eine regelmäßige Lieferung mindestens umfasst
  Die Anzahl der gelieferten Flaschen ist $n$ .
  Dann gilt: $\mu=n\cdot p$
  Im Mittel enthalten mehr als $780$ Flaschen mindestens $600 \mathrm{~ml}$ Öl $\;\Rightarrow\;\mu>780$ und $p = 1 - 0,015 = 0,985$
  ( $p$ ist hier die Gegenwahrscheinlichkeit zu der Wahrscheinlichkeit $1,5 %$ , dass sie weniger als $600 \mathrm{~ml}$ Öl enthält.)
  Damit erhältst Du folgende Ungleichung:
  $n\cdot 0{,}985>780\;\Rightarrow\;n\geq 792$
  Es müssen mindestens $792$ Flaschen geliefert werden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Löse die Ungleichung $n\cdot 0{,}985>780$ .
5. Ein Supermarkt erhält eine Lieferung von $150$ Kartons.
  Bestimmen Sie die Wahrscheinlichkeit dafür, dass mehr als $3 %$ der Kartons fehlerhaft sind. (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Bestimme die Wahrscheinlichkeit dafür, dass mehr als $3 %$ der Kartons fehlerhaft sind
  $Z$ : Anzahl der fehlerhaften Kartons
  $Z$ ist binomialverteilt mit $n = 150$ und $p=P(Y\geq 2)$
  $p=P(Y\geq 2)=\text{binomCdf}(12{,}0.015{,}2,12)\approx0{,}0134$
  $3 %$ von $150$ Kartons sind $4{,}5\;\Rightarrow\;$ mehr als $3 %$ sind demnach $5$ Kartons oder mehr, die fehlerhaft sind.
  Berechne $P(Z\geq 5)=\text{binomCdf}(150{,}0.0134{,}5,150)\approx0{,}0523$
  Die Wahrscheinlichkeit dafür, dass mehr als $3 %$ der Kartons fehlerhaft sind, beträgt rund $5 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  $Z$ : Anzahl der fehlerhaften Kartons
  $Z$ ist binomialverteilt mit $n = 150$ und $p=P(Y\geq 2)$
  Berechne $p=P(Y\geq 2)\;\Rightarrow\;p_1$
  $3 %$ von $150$ Kartons sind $4{,}5\;\Rightarrow\;$ mehr als $3 %$ sind demnach $5$ Kartons oder mehr, die fehlerhaft sind.
  Berechne $P(Z\geq 5)=\text{binomCdf}(150,p_1{,}5,150)$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

B4

Aufgabe 1

Formuliere eine passende Aufgabenstellung und erläutere den Ansatz der Rechnung

Hast du eine Frage oder Feedback?

Bestimme die Wahrscheinlichkeit, dass sich unter 100100100 Flaschen genau drei Flaschen mit weniger als 600600600 ml Öl befinden

Hast du eine Frage oder Feedback?

Ermittele die Wahrscheinlichkeit, dass die vierte geöffnete Flasche die erste überprüfte Flasche ist, die weniger als 600600600 ml Öl enthält

Hast du eine Frage oder Feedback?

Ermittele die Anzahl der Flaschen, die eine regelmäßige Lieferung mindestens umfasst

Hast du eine Frage oder Feedback?

Bestimme die Wahrscheinlichkeit dafür, dass mehr als 3 %3\;\%3% der Kartons fehlerhaft sind

Hast du eine Frage oder Feedback?

Aufgabe 2

AAA : „Die Flasche enthält mehr als 601 ml601 \mathrm{~ml}601 ml Öl.“

BBB : „Die Füllmenge der Flasche weicht höchstens um 0,5 ml0{,}5\; \mathrm{ml}0,5ml vom Erwartungswert ab.“

Hast du eine Frage oder Feedback?

Begründe, dass die Verwendung der Normalverteilung dennoch sinnvoll ist

Hast du eine Frage oder Feedback?

Begründung für Vorschlag 1, damit das Ziel des Unternehmens erreicht wird

Hast du eine Frage oder Feedback?

Aufgabe 1

Formuliere eine passende Aufgabenstellung und erläutere den Ansatz der Rechnung

Hast du eine Frage oder Feedback?

Bestimme die Wahrscheinlichkeit, dass sich unter 100100100 Flaschen genau drei Flaschen mit weniger als 600600600 ml Öl befinden

Hast du eine Frage oder Feedback?

Ermittele die Wahrscheinlichkeit, dass die vierte geöffnete Flasche die erste überprüfte Flasche ist, die weniger als 600600600 ml Öl enthält

Hast du eine Frage oder Feedback?

Ermittele die Anzahl der Flaschen, die eine regelmäßige Lieferung mindestens umfasst

Hast du eine Frage oder Feedback?

Bestimme die Wahrscheinlichkeit dafür, dass mehr als 3 %3\;\%3% der Kartons fehlerhaft sind

Hast du eine Frage oder Feedback?

Bestimme die Wahrscheinlichkeit, dass sich unter $100$ Flaschen genau drei Flaschen mit weniger als $600$ ml Öl befinden

Ermittele die Wahrscheinlichkeit, dass die vierte geöffnete Flasche die erste überprüfte Flasche ist, die weniger als $600$ ml Öl enthält

Bestimme die Wahrscheinlichkeit dafür, dass mehr als $3 %$ der Kartons fehlerhaft sind

$A$ : „Die Flasche enthält mehr als $601 \mathrm{~ml}$ Öl.“

$B$ : „Die Füllmenge der Flasche weicht höchstens um $0{,}5\; \mathrm{ml}$ vom Erwartungswert ab.“

Bestimme die Wahrscheinlichkeit, dass sich unter $100$ Flaschen genau drei Flaschen mit weniger als $600$ ml Öl befinden

Ermittele die Wahrscheinlichkeit, dass die vierte geöffnete Flasche die erste überprüfte Flasche ist, die weniger als $600$ ml Öl enthält

Bestimme die Wahrscheinlichkeit dafür, dass mehr als $3 %$ der Kartons fehlerhaft sind