Fruchtfliegen
Jasmin möchte für ein Biologieprojekt untersuchen, wie schnell sich
Fruchtfliegen (Abbildung 1) vermehren. Sie kauft im Zoo-Center drei Zuchtboxen und bezeichnet diese mit A, B und C.

Zuchtbox A enthält anfänglich zehn Fruchtfliegen. Jasmin bewahrt die Box in ihrem warmen Zimmer auf und protokolliert in den folgenden Tagen die Anzahl der Tiere in der Box (Abbildung 2).
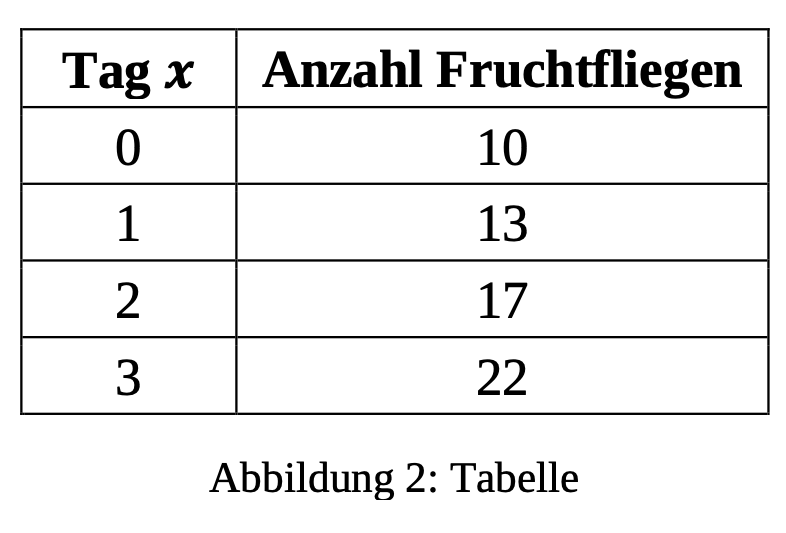
Die Anzahl der Fruchtfliegen in Zuchtbox A wächst täglich um ca. . Weise dies für den Übergang von Tag 0 auf Tag 1 nach. (2BE)
Jasmin stellt die Funktion mit der Funktionsgleichung auf, um die Anzahl der Fruchtfliegen am Tag zu berechnen.
Bestimme die voraussichtliche Anzahl an Fruchtfliegen nach 30 Tagen. (2BE)
Bestimme, nach wie vielen Tagen die Anzahl der Fruchtfliegen erstmals größer als sein müsste. (3BE)
Zuchtbox B enthält anfänglich 20 Fruchtfliegen . Jasmin bewahrt diese im kühleren Keller auf und stellt fest, dass sich die Fruchtfliegen dort langsamer vermehren als in ihrem warmen Zimmer. Zur Berechnung der Anzahl der Fruchtfliegen am Tag in der zweiten Box nutzt Jasmin die Funktion mit , mit .
In Abbildung 3 sind die Graphen und dargestellt. Begründe, dass die Funktion mit durch Graph dargestellt wird und die Funktion mit durch Graph dargestellt wird. (3BE)
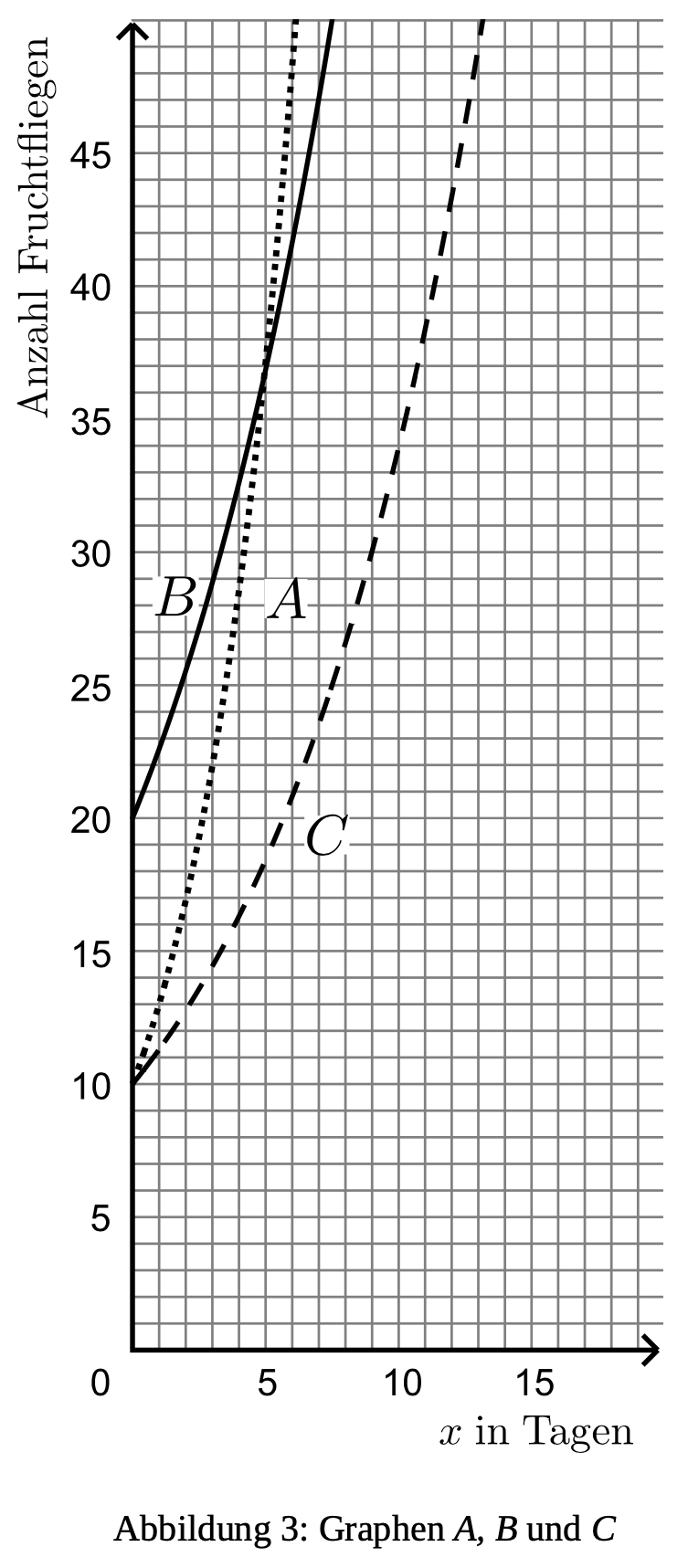
Bestimme mithilfe von Abbildung 3 den Tag, an dem die Zuchtboxen A und B etwa gleich viele Fruchtfliegen enthalten und gib die Anzahl an. (2BE)
Jasmin führt ein drittes Experiment mit Zuchtbox C durch. Die Entwicklung der Anzahl an Fruchtfliegen wird mit dem Graphen beschrieben. Bestimme für den Graphen näherungsweise die Funktionsgleichung mit . (3BE)
Stelle eine begründete Vermutung zu den Bedingungen auf, unter denen das Experiment mit Zuchtbox C durchgeführt wurde, indem du die drei abgebildeten Graphen vergleichst. (3BE)
