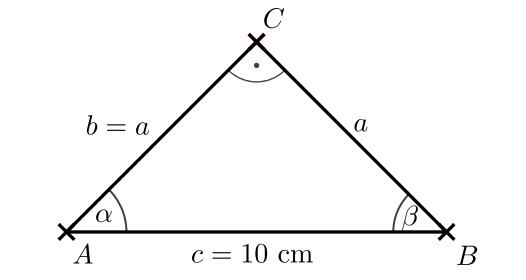
Dreieck
Abbildung 1 zeigt das Dreieck mit vorgegebenen Maßangaben.
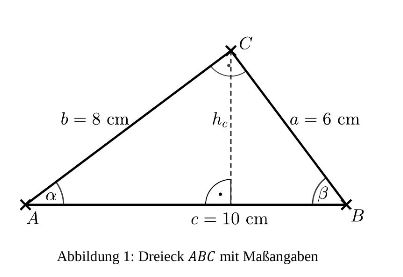
Zeige rechnerisch, dass der Flächeninhalt dieses Dreiecks groß ist.
Begründe, dass die folgende Gleichung gilt:
Bestimme rechnerisch die Länge der Strecke .
Bestimme rechnerisch die Größe des Winkels .
Gegeben ist ein gleichschenkliges rechtwinkliges Dreieck mit der Basis und den beiden Schenkeln und . (1) Skizziere eine geeignete Planfigur. (2) Berechne die Länge der Schenkel.
Kai behauptet: „Es gibt auch ein rechtwinkliges Dreieck, bei dem alle drei Seiten gleich lang sind." Entscheide begründet, ob Kais Behauptung stimmt.
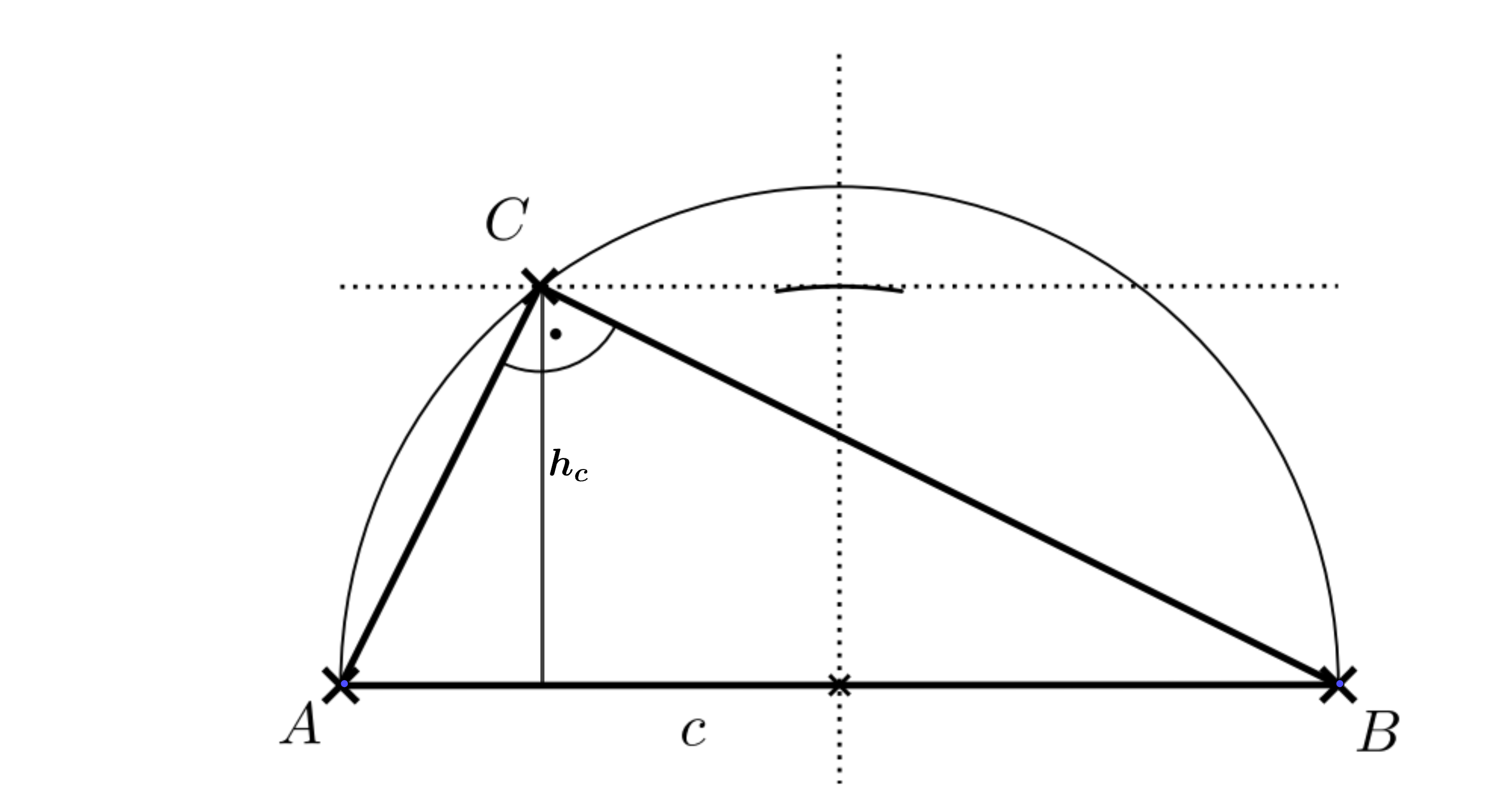
Konstruiere mithilfe des Satz des Thales ein rechtwinkliges Dreieck mit der Hypotenuse und der Höhe .