Aufgabe 6
Eine Zufallsgröße ist binomialverteilt mit .
Das unvollständige Histogramm der Verteilung ist in Abbildung 3 dargestellt.
Es gilt: .
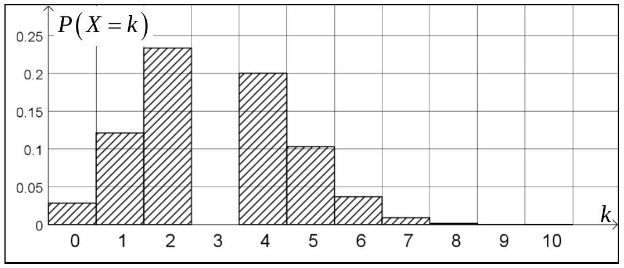
Abbildung 3
(i) Ermitteln Sie näherungsweise die Wahrscheinlichkeit . (1 P)
(ii) Ermitteln Sie näherungsweise die Wahrscheinlichkeit . (1 P)
Die Histogramme I bis III in den Abbildungen 4-1 bis 4-3 zeigen Ausschnitte aus Wahrscheinlichkeitsverteilungen von drei binomialverteilten Zufallsgrößen und .
Zu den Zufallsgrößen gehören die folgenden Werte für die Parameter und :
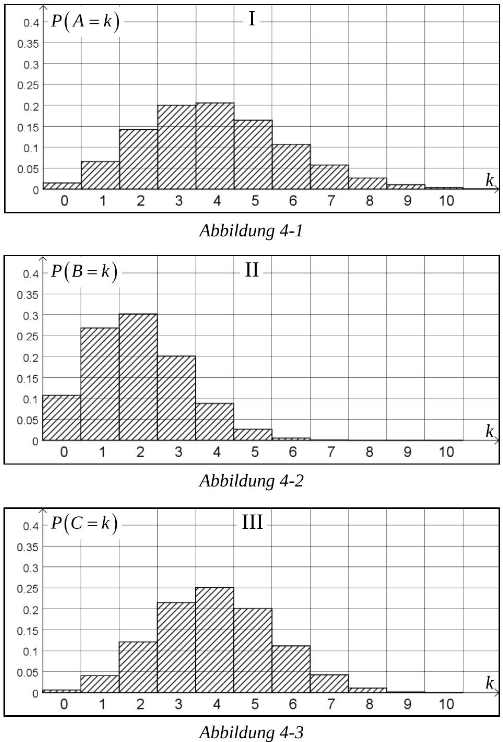
Ordnen Sie den Histogrammen I bis III die passenden Werte von und zu und begründen Sie Ihre Zuordnung. (3 P)
