Aufgabe 2
Die folgende Aufgabe ist eine Fortsetzung der Aufgabe 1.
Abbildung 1 zeigt schematisch die achsensymmetrische Seitenansicht einer Hängebrücke. Die beiden vertikalen Pfeiler haben einen Abstand von . Die Wasseroberfläche liegt unterhalb der Fahrbahn.
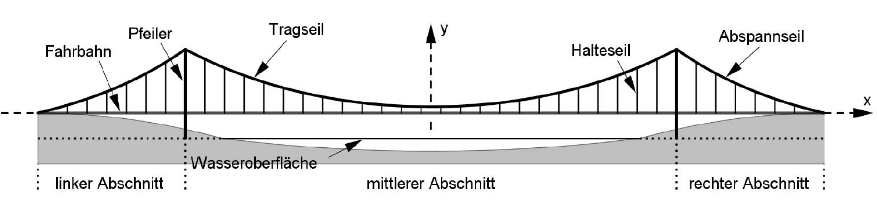
Abbildung 1
Die beiden Pfeiler gliedern die Brücke in einen linken, einen mittleren und einen rechten Abschnitt. Am oberen Ende jedes Pfeilers ist sowohl das Tragseil des mittleren Abschnitts als auch das Abspannseil des linken bzw. rechten Abschnitts befestigt. Die beiden Abspannseile sind am jeweiligen Ende der Fahrbahn verankert.
Im verwendeten Koordinatensystem entspricht eine Längeneinheit in der Realität. In der Seitenansicht der Brücke verläuft die x-Achse entlang der horizontal verlaufenden Fahrbahn, die y-Achse entlang der Symmetrieachse.
Im Folgenden wird der mittlere Abschnitt der Brücke betrachtet. Die vertikal verlaufenden Halteseile verbinden die Fahrbahn mit dem Tragseil. Sie haben sowohl von den Pfeilern als auch untereinander einen horizontalen Abstand von .
Der Verlauf des Tragseils wird modellhaft durch den Funktionsterm beschrieben.
Begründen Sie, dass der Term von damit in Einklang steht, dass die Seitenansicht der Brücke achsensymmetrisch ist. (2 P)
Zwei der Halteseile im mittleren Brückenabschnitt haben eine Länge von jeweils .
Zeigen Sie rechnerisch, dass sich diese Halteseile im Modell an den Stellen und befinden, d. h. links bzw. rechts der Brückenmitte.
Geben Sie außerdem an, an wievielter Position von der Brückenmitte aus sich diese Halteseile befinden. (2 P)
Zwei Punkte des Tragseils in der rechten Hälfte des mittleren Abschnitts haben einen horizontalen Abstand von und einen Höhenunterschied von .
Geben Sie eine Gleichung an, deren Lösung die x-Koordinate des höher liegenden Punkts im Modell ist. (2 P)
Geben Sie die Bedeutung des Terms
im Sachzusammenhang an und begründen Sie Ihre Angabe. (4 P)

