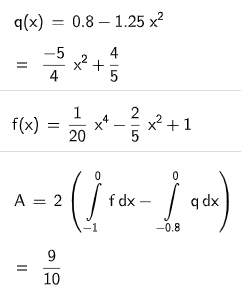B5

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Die Abbildung zeigt modellhaft den Längsschnitt einer dreiteiligen Brücke aus Holz für eine Spielzeugeisenbahn. Die Züge können sowohl über die Brücke fahren als auch darunter hindurch.
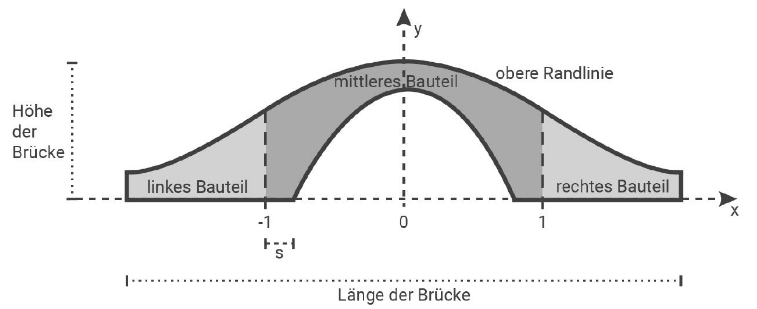
Abbildung
Die obere Randlinie des Längsschnitts der Brücke kann mithilfe des Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)=\frac{1}{20} x^{4}-\frac{2}{5} x^{2}+1$ beschrieben werden. Dabei werden die Endpunkte dieser Randlinie durch die beiden Tiefpunkte des Graphen von $f$ dargestellt. Im verwendeten Koordinatensystem beschreibt die $x$ -Achse die Horizontale; eine Längeneinheit entspricht einem Dezimeter in der Realität.
1. Begründen Sie, dass die obere Randlinie achsensymmetrisch zur $y$ -Achse ist. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
  Begründe, dass die obere Randlinie achsensymmetrisch zur $y$ -Achse ist
  Gegeben ist $f(x)=\frac{1}{20} x^{4}-\frac{2}{5} x^{2}+1$ . Es treten nur gerade Exponenten auf. Der Graph von $f$ ist symmetrisch zur y-Achse.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es treten bei der Funktion $f$ nur gerade Exponenten auf. Was bedeutet das für die Symmetrie?
2. Bestimmen Sie rechnerisch die Höhe und die Länge der Brücke (vgl. Abbildung). $[$ Kontrolllösung: Ein Tiefpunkt des Graphen von $f$ hat die $x$ -Koordinate $2$ $]$ (5 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
  Bestimme rechnerisch die Höhe und die Länge der Brücke
  Höhe
  Die Höhe der Brücke entspricht dem y-Achsenabschnitt von $f$ .
  $\Rightarrow\;f(0)=1$
  Die Höhe der Brücke beträgt $1\mathrm{~dm}$ .
  Länge
  Berechne die Koordinaten des Tiefpunktes:
  Die notwendige Bedingung für ein Extremum ist $f^{'} (x) = 0$ .
  Berechne $f^{'} (x)$ :
  $f'(x)=\dfrac{4}{20} x^{3}-\dfrac{4}{5} x=\dfrac{1}{5}\cdot x \cdot\left(x^2-4\right)$
  $f'(x)=0\;\Rightarrow\;0=\dfrac{1}{5}\cdot x \cdot\left(x^2-4\right)$
  Es folgt mit dem Satz vom Nullprodukt:
  $x=0\vee x=\pm 2$
  An den Stellen $x = - 2, x = 0$ und $x = 2$ liegen Extremstellen vor.
  Die hinreichende Bedingung für ein Extremum ist $f''(x)\neq 0$ .
  Berechne $f^{''} (x)$ :
  $f''(x)=\dfrac{3}{5} x^{2}-\dfrac{4}{5}$
  Setze die berechneten Extremstellen ein:
  $f''(0)=-\dfrac{4}{5}<0\;\Rightarrow\; HP$
  $f''(-2)=\dfrac{3}{5} (-2)^{2}-\dfrac{4}{5}=\dfrac{8}{5}>0\;\Rightarrow\;TP$
  $f''(2)=\dfrac{3}{5} 2^{2}-\dfrac{4}{5}=\dfrac{8}{5}>0\;\Rightarrow\;TP$
  An den Stellen $x = - 2$ bzw. $x = 2$ liegen die Tiefpunkte des Graphen von $f$ .
  $\Rightarrow\;$ Länge der Brücke entspricht dem Abstand der x-Koordinaten der beiden Tiefpunkte $l = 2 - (- 2) = 4$
  Die Länge der Brücke beträgt $4\mathrm{~dm}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Die Höhe der Brücke entspricht dem y-Achsenabschnitt von $f$ .
  Teil 2
  Berechne die Koordinaten des Tiefpunktes.
3. Geben Sie die Bedeutung des Terms $\frac{f(2)-f(1)}{2-1}$ im Sachzusammenhang an und bestimmen Sie seinen Wert. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Differenzenquotient
  Gib die Bedeutung des Terms $\frac{f(2)-f(1)}{2-1}$ im Sachzusammenhang an
  Der Term $\frac{f(2)-f(1)}{2-1}$ ist ein Differenzenquotient. Mit ihm wird die mittlere Steigung der oberen Randlinie im Intervall $[1; 2]$ berechnet.
  Bestimme seinen Wert
  Es gilt:
  $f(2)=\dfrac{1}{20} 2^{4}-\dfrac{2}{5} 2^{2}+1=\dfrac{16}{20}-\dfrac{8}{5}+1=\dfrac{1}{5}=0{,}2$ und
  $f(1)=\dfrac{1}{20} 1^{4}-\dfrac{2}{5} 1^{2}+1=\dfrac{1}{20}-\dfrac{2}{5}+1=\dfrac{13}{20}=0{,}65$ .
  Berechne $\dfrac{f(2)-f(1)}{2-1}=\dfrac{0{,}2-0{,}65}{1}=-0{,}45$ .
  Der Wert des Terms beträgt $- 0,45$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Was ist ein Differenzenquotient im Sachzusammenhang?
  Teil 2
  Berechne $f (2)$ und $f (1)$ und setze in den gegebenen Term ein.
4. Bestimmen Sie die größte Steigung der Brücke, die beim Überfahren zu überwinden ist. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
  Bestimme die größte Steigung der Brücke, die beim Überfahren zu überwinden ist
  Die 1. Ableitung muss maximal werden:
  $f'(x=\dfrac{1}{5} x^{3}-\dfrac{4}{5} x$
  Lasse Dir den Graphen von $f^{'} (x)$ anzeigen und bestimme das Maximum:
  Man erhält $x_M\approx-1{,}1547...$ und $y_M\approx0{,}61584...\;\Rightarrow\;HP(-1{,}155\mid 0{,}616)$
  Die größte Steigung der Brücke, die beim Überfahren zu überwinden ist, ist $f'(1{,}155)\approx 0{,}616$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die 1. Ableitung muss maximal werden. Berechne $f^{'} (x)$ .
  Lasse Dir den Graphen von $f^{'} (x)$ anzeigen und bestimme das Maximum.
  Der y-Wert des Hochpunktes ist die gesuchte Steigung.
5. Der parabelförmige Teil der unteren Randlinie des Längsschnitts der Brücke kann mithilfe des Graphen einer in $\mathbb{R}$ definierten Funktion $q_{a}$ mit $q_{a}(x)=0{,}8-a \cdot x^{2}$ mit $a \in \mathbb{R}, a>0$ , beschrieben werden.
  In der Abbildung ist die Länge einer der beiden Bodenflächen des mittleren Bauteils mit $s$ bezeichnet. Bestimmen Sie den Wert von $a$ , für den $s=0{,}1 \mathrm{~dm}$ gilt. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
  Bestimme den Wert von $a$ , für den $s=0{,}1 \mathrm{~dm}$ gilt
  Wenn $s = 0,1$ ist, dann muss $x = - 1 + 0,1 = - 0,9$ sein.
  Berechne für $x = - 0,9$ die Nullstelle von $q_{a}(x)=0{,}8-a \cdot x^{2}$ .
  $\Rightarrow\;0=0{,}8-a \cdot (-0{,}9)^{2}\;\Rightarrow\;0=0{,}8-0{,}81\cdot a\;\Rightarrow\;a=\dfrac{0{,}8}{0{,}81}=\dfrac{80}{81}\approx0{,}988$
  Somit ist für $a = 0,988$ die Länge $s=0{,}1 \mathrm{~dm}$ lang.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Wenn $s = 0,1$ ist, dann muss $x = - 1 + 0,1 = - 0,9$ sein.
  Berechne für $x = - 0,9$ die Nullstelle von $q_{a}(x)=0{,}8-a \cdot x^{2}$ und löse nach a auf.
6. Begründen Sie im Sachzusammenhang, dass für die Beschreibung der unteren Randlinie beliebig große Werte von $a$ nicht infrage kommen. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Einfluss der Parameter in der Scheitelform
  Begründe im Sachzusammenhang, dass für die Beschreibung der unteren Randlinie beliebig große Werte von $a$ nicht infrage kommen
  Je größer $a$ wird, umso kleiner wird die Breite der Durchfahrt für die Züge (der Graph von $q_{a}$ wird schmaler).
  Die Öffnungsbreite muss größer als die Breite des Zuges sein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Was passiert, wenn $a$ größer wird.
  Kann der Zug dann noch durch die Brücke fahren?
7. Für die Brücke gilt $a = 1,25$ . Die drei Bauteile der Brücke werden aus massivem Holz hergestellt; $1 \mathrm{~dm}^{3}$ des Holzes hat eine Masse von $800$ Gramm. Die Brücke ist $0{,}4 \mathrm{~dm}$ breit.
  Bestimmen Sie die Nullstellen von $q_{1{,}25}$ und ermitteln Sie die Masse des mittleren Bauteils. (5 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Bestimme die Nullstellen von $q_{1{,}25}$
  $q_{1{,}25}(x)=0{,}8-1{,}25 \cdot x^{2}$
  Berechne die Nullstellen von $q_{a}$ :
  $0=0{,}8-1{,}25 \cdot x^{2}\;\Rightarrow\;x^2=\dfrac{0{,}8}{1{,}25}=0{,}64\;\Rightarrow\;x=\pm 0{,}8$ .
  Die Nullstellen von $q_{1{,}25}$ sind $x_1=-0{,}8$ und $x_2=0{,}8$ .
  Ermittle die Masse des mittleren Bauteils
  Bekannt sind: Für die Brücke gilt $a = 1,25$ . Die drei Bauteile der Brücke werden aus massivem Holz hergestellt; $1 \mathrm{~dm}^{3}$ des Holzes hat eine Masse von $800$ Gramm. Die Brücke ist $0{,}4 \mathrm{~dm}$ breit.
  Berechne den Flächeninhalt des mittleren Bauteils. (Beachte, dass das Flächenstück symmetrisch zur y-Achse ist.):
  $A=2\cdot \left(\displaystyle\int_{-1}^0 f(x)\;\mathrm{d}x-\displaystyle\int_{-0{,}8}^0 q_{1{,}25}(x)\;\mathrm{d}x\right)$
  Der Flächeninhalt des mittleren Bauteils beträgt $A=0{,}9\mathrm{~dm}^{2}$ .
  Da die Brücke $0{,}4 \mathrm{~dm}$ breit ist, berechnet man das Volumen mit: $V=A\cdot 0{,}4=0{,}9\cdot 0{,}4=0{,}36$
  Das Volumen beträgt $0{,}36\mathrm{~dm}^{3}$ .
  $1 \mathrm{~dm}^{3}$ des Holzes hat eine Masse von $800$ Gramm.
  Die Masse des mittleren Bauteils ist dann $m=V\cdot 800=0{,}36\cdot 800=288$ .
  Die Masse des mittleren Bauteils beträgt $m=288\mathrm{~g}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Es ist $q_{1{,}25}(x)=0{,}8-1{,}25 \cdot x^{2}$ .
  Berechne die Nullstellen von $q_{a}$ $\;\Rightarrow\;x_1, x_2$ . ( $x_{1}$ ist die linke Nullstelle.)
  Teil 2
  Der Flächeninhalt des mittleren Bauteils berechnet man mit $A=2\cdot \left(\displaystyle\int_{-1}^0 f(x)\;\mathrm{d}x-\displaystyle\int_{x_1}^0 q_{1{,}25}(x)\;\mathrm{d}x\right)$ (Beachte dabei, dass das Flächenstück symmetrisch zur y-Achse ist.) $\;\Rightarrow\;A$ in $\mathrm{dm}^2$ .
  Da die Brücke $0{,}4 \mathrm{~dm}$ breit ist, berechnet man das Volumen mit $V=A\cdot 0{,}4$ .
  Die Masse des mittleren Bauteils in Gramm berechnet man mit $m=V\cdot 800$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

B5

Aufgabe 1

Begründe, dass die obere Randlinie achsensymmetrisch zur yyy-Achse ist

Hast du eine Frage oder Feedback?

Bestimme rechnerisch die Höhe und die Länge der Brücke

Hast du eine Frage oder Feedback?

Gib die Bedeutung des Terms f(2)−f(1)2−1\frac{f(2)-f(1)}{2-1}2−1f(2)−f(1)​ im Sachzusammenhang an

Bestimme seinen Wert

Hast du eine Frage oder Feedback?

Bestimme die größte Steigung der Brücke, die beim Überfahren zu überwinden ist

Hast du eine Frage oder Feedback?

Bestimme den Wert von aaa, für den s=0,1 dms=0{,}1 \mathrm{~dm}s=0,1 dm gilt

Hast du eine Frage oder Feedback?

Begründe im Sachzusammenhang, dass für die Beschreibung der unteren Randlinie beliebig große Werte von aaa nicht infrage kommen

Hast du eine Frage oder Feedback?

Bestimme die Nullstellen von q1,25q_{1{,}25}q1,25​

Ermittle die Masse des mittleren Bauteils

Hast du eine Frage oder Feedback?

Begründe, dass die obere Randlinie achsensymmetrisch zur $y$ -Achse ist

Gib die Bedeutung des Terms $\frac{f(2)-f(1)}{2-1}$ im Sachzusammenhang an

Bestimme den Wert von $a$ , für den $s=0{,}1 \mathrm{~dm}$ gilt

Begründe im Sachzusammenhang, dass für die Beschreibung der unteren Randlinie beliebig große Werte von $a$ nicht infrage kommen

Bestimme die Nullstellen von $q_{1{,}25}$