Melina und Paul besitzen Fußball-Sammelbilder. In Pauls Schuhkarton liegen 20 Sammelbilder von Nationalspielern.
Die Tabelle zeigt deren Verteilung auf drei Nationalmannschaften.
Nationalmannschaft | Frankreich | Deutschland | Portugal |
|---|---|---|---|
Anzahl der Sammelbilder |
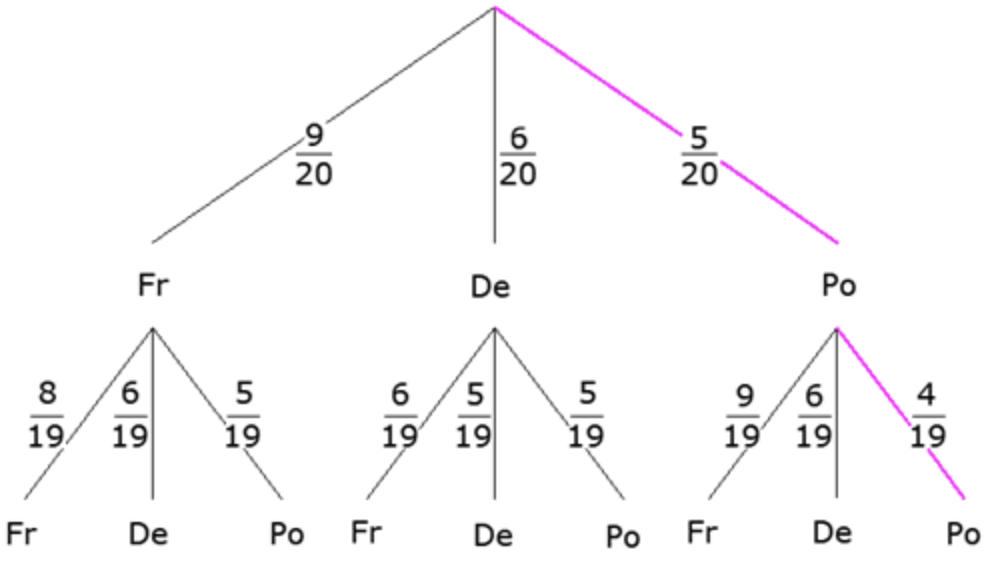
Melina zieht zwei Sammelbilder gleichzeitig.
Wie groß ist die Wahrscheinlichkeit, dass auf den beiden gezogenen Sammelbildern
- portugiesische Spieler abgebildet sind?
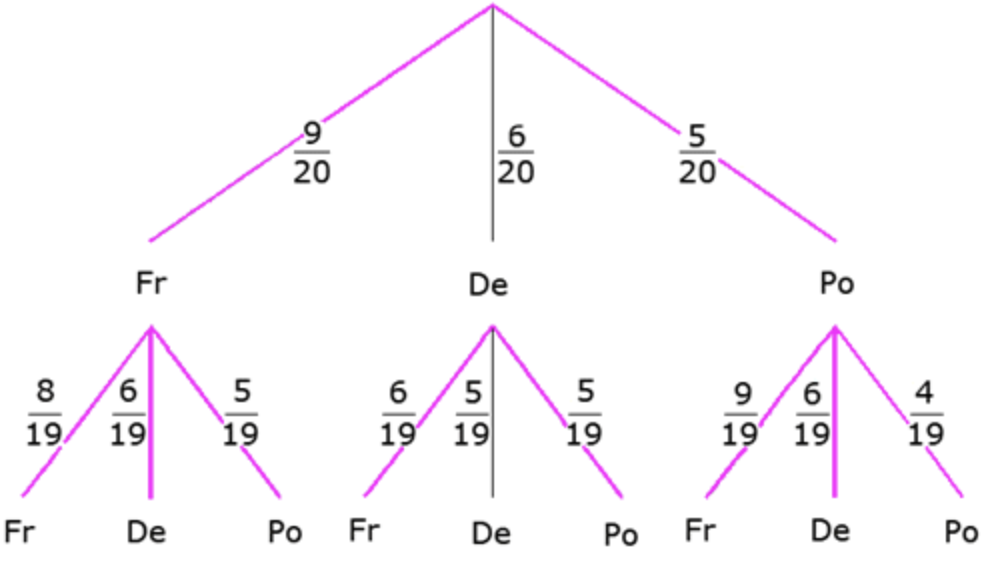
- höchstens ein deutscher Spieler abgebildet ist?
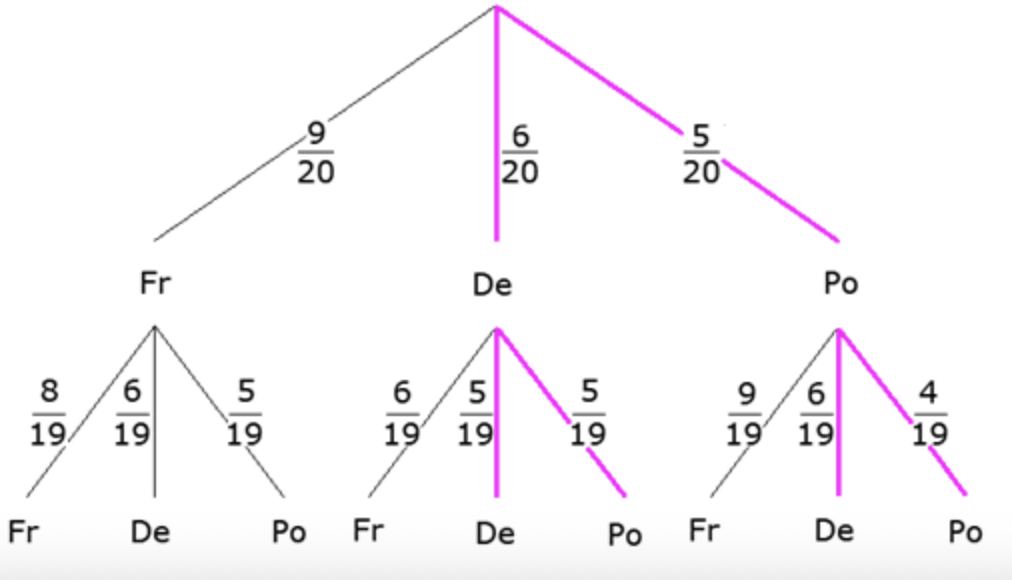
- kein französischer Spieler abgebildet ist?
[3 Pkte]