Wahlteil B - lernen mit Serlo!

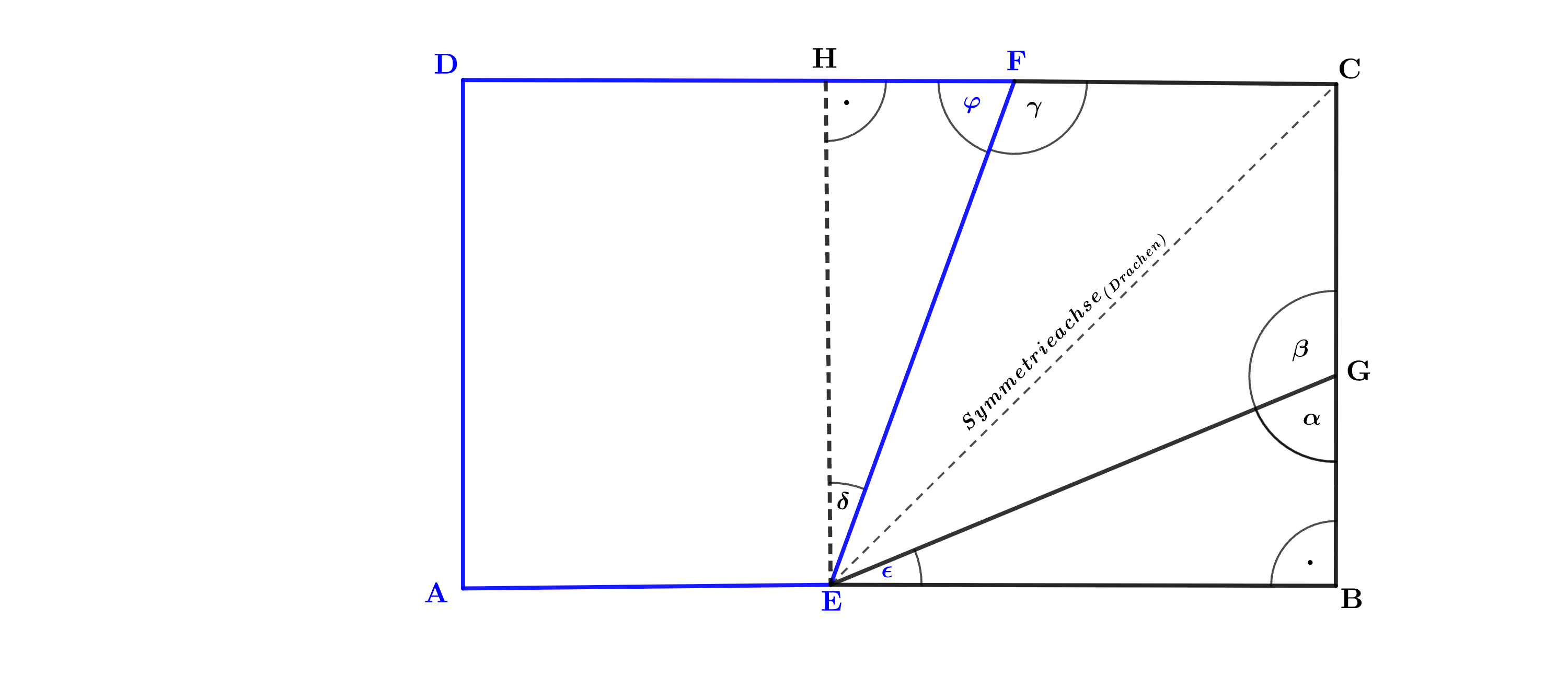
Im Rechteck $A B C D$ liegt das Drachenviereck $E G C F$ .
Es gilt:
$\begin{aligned} A B & = 9,4 c m \\ B E & = 5,6 c m \\ ε & = {20,0}^{\circ} \end{aligned}$
Berechne den Winkel $φ$ . Berechne den Umfang des Vierecks $A E F D$ .
[5 Pkte]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens im rechtwinkligen Dreieck
Berechnen des Winkels $φ$ .
Berechnen von $α$ :
$\begin{array}{l} α = 90 ° - ϵ \\ α = 90 ° - 20 ° \\ α = 70 ° \end{array}$
Berechnen von $β$ :
$\begin{array}{l} β = 180 ° - α \\ β = 180 ° - 70 ° \\ β = 110 ° \end{array}$
$β = γ$ wegen Achsensymmetrie des Drachenvierecks.
Der Winkel $φ$ ist dann:
$\begin{array}{l} φ = 180 ° - 110 ° \\ φ = 70 ° \end{array}$
Berechnen des Umfangs des Vierecks $AEFD$ .
Umfang des Vierecks $AEFD$ :
$U_{A E F D} = A E + E F + F H + D H + A D$
$\begin{array}{l} A E = A B - B E \\ A E = 9,4 - 5,6 \\ A E = 3,8 cm \end{array}$
$E G = E F$ und $B E = E H$ wegen Achsensymmetrie des Drachenvierecks.
Wir berechnen $E G$ mithilfe des Kosinus.
$\cos ϵ = \frac{B E}{E G} \Rightarrow E G = \frac{B E}{\cos ϵ}$
$E G = \frac{5,6}{c o s 20 °}$
$E G = \frac{5,6}{0,9397}$
$E G = 5,96 cm$
Jetzt müssen wir noch $F H$ berechnen, dann können wir den Umfang
des Vierecks $AEFD$ berechnen.
Wir berechnen $F H$ mithilfe des Tangens.
$\cos φ = \frac{F H}{E F} \Rightarrow F H = E F \cdot \cos φ$
$F H = 5,96 \cdot \cos 70 °$
$F H = 5,96 \cdot 0,3420$
$F H \approx 2,04 cm$
$U_{A E F D} = 3,8 + 5,96 + 2,04 + 3,8 + 5,6$
$U_{A E F D} = 21,2 cm$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne den Winkel $α$ .
Berechne den Winkel $β$ .
Berechne den Winkel $γ$ .
Berechne den Winkel $φ$ .
Berechne den Umfang des Vierecks $AEFD$ .
Die Parabeln $p_{1}$ und $p_{2}$ sind zwei nach oben geöffnete verschobene Normalparabeln. Die Parabel $p_{1}$ hat den Scheitelpunkt $S_{1} (1 | 1)$ . Die Parabel $p_{2}$ schneidet die $x$ -Achse in den Punkten $N_{1} (- 6 | 0)$ und $N_{2} (- 2 | 0)$ . Bestimme die Funktionsgleichungen von $p_{1}$ und $p_{2}$ .
Die Gerade $g$ verläuft durch den Scheitelpunkt $S_{1}$ und den Punkt $A (2 | - 1)$ . Berechne die Funktionsgleichung von $g$ .
Der Punkt $S_{2}$ ist der Scheitelpunkt der Parabel $p_{2}$ . Berechne die Entfernung zwischen $S_{1}$ und $S_{2}$ .
Milo behauptet: „Die Parabeln $p_{1}$ und $p_{2}$ sowie die Gerade $g$ schneiden sich in einem gemeinsamen Punkt."
Überprüfe diese Behauptung. Begründe deine Antwort rechnerisch.
[5 Pkte]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen - Parabeln
Bestimmen der Funktionsgleichungen von $p_{1}$ und $p_{2}$ .
Bestimmen der Funktionsgleichung von $p_{1}$ .
Die allgemeine Scheitelform lautet:
$f (x) = a (x - d)^{2} + e$
Folgende Werte sind aus der Aufgabenstellung bekannt:
$d = 1$
$e = 1$
$a = 1$ (da es sich hier um eine nach oben geöffnete Normalparabel handelt)
Einsetzen der bekannten Werte in die allgemeine Scheitelform:
$p_{1} (x) = (x - 1)^{2} + 1$ ausmultiplizieren
$p_{1} (x) = x^{2} - 2 x + 2$
Bestimmen der Funktionsgleichng von $p_{2}$ .
Die allgemeine Linearfaktordarstellung lautet:
$f (x) = a (x - x_{1}) (x - x_{2})$
Folgende Werte sind aus der Aufgabenstellung bekannt:
$x_{1} = - 6$
$x_{2} = - 2$
$a = 1$ (da es sich hier um eine nach oben geöffnete Normalparabel handelt)
Einsetzen der bekannten Werte in die allgemeine Linearfaktordarstellung:
$p_{2} (x) = (x + 6) (x + 2)$ ausmultiplizieren
$p_{2} (x) = x^{2} + 8 x + 12$
Berechnen der Funktionsgleichung von $g$ .
Die allgemeine Geradengleichung lautet:
$y = m \cdot x + t$
Folgende Werte sind aus der Aufgabenstellung bekannt:
$A (2 | - 1)$
$S_{1} (1 | 1)$
Wir berechnen die Steigung $m$ .
Die Formel zur Berechnung der Steigung $m$ lautet:
$m = \frac{y_{Δ}}{x_{Δ}} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$
Einstezen der bekannten Werte in die Formel:
$m = \frac{1 - (- 1)}{1 - 2} \Rightarrow m = - 2$
Berechnen von $t$ .
$1 = - 2 + t \Rightarrow t = 3$
Die Funktionsgleichung von $g$ lautet dann:
$g : y = - 2 x + 3$
Berechnen der Entfernung zwischen $S_{1}$ und $S_{2}$ .
Ermitteln des Scheitelpunktes der Parabel $p_{2}$ .
Berechnen des Scheitelpunktes mit der Formel:
$S (- \frac{b}{2 \cdot a} | c - \frac{b^{2}}{4 \cdot a})$
Folgende Werte sind bekannt $($ siehe Funktionsgleichung $p_{2} (x)$ $)$ :
$a = 1$
$b = 8$
$c = 12$
Einsetzen der Werte in die Formel:
$S_{2} (- \frac{8}{2 \cdot 1} | 12 - \frac{8^{2}}{4 \cdot 1})$
$S_{2} (- \frac{8}{2} | 12 - \frac{64}{4})$
$S_{2} (- 4 | - 4)$
Berechnen des Abstandes $a$ mit dem Satz des Pythagoras:
$a^{2} = (x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}$
$a = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$
$a = \sqrt{(- 4 - 1)^{2} + (- 4 - 1)^{2}}$
$a = \sqrt{50}$
$a \approx 7,07 L E$
Überprüfen von Milas Behauptung.
x
$- 2$
$- 1$
$0$
$1$
$2$
$p_{1}$
$10$
$5$
$2$
$1$
$2$
$p_{2}$
$0$
$5$
$12$
$21$
$32$
$g$
$7$
$5$
$3$
$1$
$- 1$
Milo hat Recht, die Parabeln $p_{1}$ und $p_{2}$ sowie die Gerade $g$ haben einen gemeinsamen Schnittpunkt $P_{g e m .}$ mit den Koordinaten $P_{g e m .} (- 1 | 5)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Stelle die Scheitelform von $p_{1}$ auf.
Multipliziere die Scheitelform aus.
Bestimme die Funktionsgleichung von $p_{2}$ , setze die Nullstellen $N_{1}$ und $N_{2}$ in die Linearfaktordarstellung ein und multipliziere aus.
Ermittle die Geradengleichung, indem Du die Koordinaten der Punkte $S_{2}$ und $A$ in die allgemeine Geradengleichung einsetzt.
Berechne die Entfernung zwischen $S_{1}$ und $S_{2}$ . Wende den Satz des Pythagoras an.

x	$- 2$	$- 1$	$0$	$1$	$2$
$p_{1}$	$10$	$5$	$2$	$1$	$2$
$p_{2}$	$0$	$5$	$12$	$21$	$32$
$g$	$7$	$5$	$3$	$1$	$- 1$

Dieses Werk wurde vom Land Baden-Württemberg zur Verfügung gestellt. → Was bedeutet das?

Berechnen des Winkels φ.

Berechnen des Umfangs des Vierecks AEFD.

Hast du eine Frage oder Feedback?

Bestimmen der Funktionsgleichungen von p1 und p2.

Berechnen der Funktionsgleichung von g.

Berechnen der Entfernung zwischen S1 und S2.

Überprüfen von Milas Behauptung.

Hast du eine Frage oder Feedback?

Berechnen des Winkels $φ$ .

Berechnen des Umfangs des Vierecks $AEFD$ .

Bestimmen der Funktionsgleichungen von $p_{1}$ und $p_{2}$ .

Berechnen der Funktionsgleichung von $g$ .

Berechnen der Entfernung zwischen $S_{1}$ und $S_{2}$ .