Wahlteil B

🎓 Prüfungsbereich für Baden-Württemberg

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
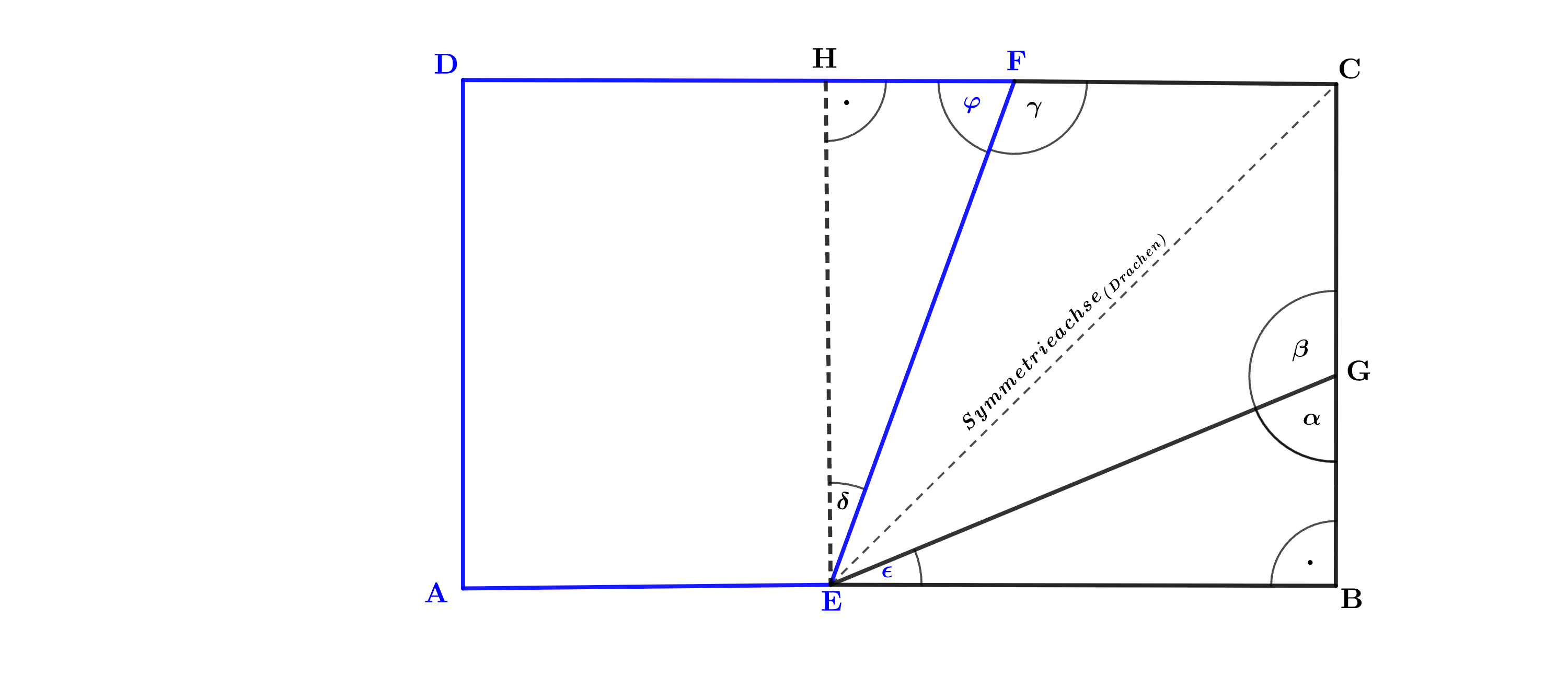
1. Im Rechteck $A B C D$ liegt das Drachenviereck $E G C F$ .
  Es gilt:
  $\def\arraystretch{1.25} \begin{aligned} \overline{A B} & =9{,}4 \mathrm{~cm} \\ \overline{B E} & =5{,}6 \mathrm{~cm} \\ \varepsilon & =20{,}0^{\circ} \end{aligned}$
  Berechne den Winkel $\varphi$ . Berechne den Umfang des Vierecks $A E F D$ .
  [5 Pkte]
2. Die Parabeln $p_{1}$ und $p_{2}$ sind zwei nach oben geöffnete verschobene Normalparabeln. Die Parabel $p_{1}$ hat den Scheitelpunkt $S_{1}(1 \mid 1)$ . Die Parabel $p_{2}$ schneidet die $x$ -Achse in den Punkten $N_{1}(-6 \mid 0)$ und $N_{2}(-2 \mid 0)$ . Bestimme die Funktionsgleichungen von $p_{1}$ und $p_{2}$ .
  Die Gerade $g$ verläuft durch den Scheitelpunkt $S_{1}$ und den Punkt $A(2 \mid-1)$ . Berechne die Funktionsgleichung von $g$ .
  Der Punkt $S_{2}$ ist der Scheitelpunkt der Parabel $p_{2}$ . Berechne die Entfernung zwischen $S_{1}$ und $S_{2}$ .
  Milo behauptet: „Die Parabeln $p_{1}$ und $p_{2}$ sowie die Gerade $g$ schneiden sich in einem gemeinsamen Punkt."
  Überprüfe diese Behauptung. Begründe deine Antwort rechnerisch.
  [5 Pkte]
2
1. Die Gerade $g$ hat die Funktionsgleichung $y = - x - 3$ .
  Sie schneidet die $x$ -Achse im Punkt $A$ und die $y$ -Achse im Punkt $B$ . Bestimme die Koordinaten der Punkte $A$ und $B$ .
  Durch die Punkte $A$ und $B$ verläuft die nach oben geöffnete verschobene Normalparabel $p$ . Berechne die Funktionsgleichung der Parabel $p$ und die Koordinaten ihres Scheitelpunktes $S$ .
  Die beiden Punkte $P\left(x_{P} \mid 12\right)$ und $Q\left(x_{Q} \mid 12\right)$ liegen auf der Parabel $p$ . Sie bilden zusammen mit dem Scheitelpunkt $S$ das Dreieck $P S Q$ . Berechne den Flächeninhalt des Dreiecks $P S Q$ .
  [5 Pkte]
2. Die Abbildung zeigt den Achsenschnitt eines zusammengesetzten Körpers und den Parallelschnitt einer quadratischen Pyramide.
  Der zusammengesetzte Körper besteht aus einer Halbkugel und einem Kegel.
  Es gilt:
  $\def\arraystretch{1.25} \begin{aligned} s & =14{,}4 \mathrm{~cm} \\ \delta & =42{,}0^{\circ} \\ h_{\mathrm{ges}} & =h_{\mathrm{Pyr}} \end{aligned}$
  Der Durchmesser $d$ des zusammengesetzten Körpers ist genauso lang wie die Grundkante $a$ der quadratischen Pyramide.
  Berechne die Differenz der Oberflächeninhalte der beiden Körper.
  [5 Pkte]
3
1. Beim Schulfest bietet die Klasse 10a ein Angelspiel an. Dabei dürfen die Spieler zweimal nacheinander einen Gegenstand aus einem Gefäß angeln. Die Gegenstände werden nicht zurückgelegt. In dem Gefäß liegen fünf Fische, drei Seesterne und zwei Muscheln.
  Berechne die Wahrscheinlichkeit für das Ereignis „zweimal Muschel".
  Für ein Glücksspiel wird der gegebene Gewinnplan eingesetzt.
  Ereignis
  Gewinn
  zweimal Muschel
  $9,00$ €
  zweimal Seestern
  $4,00$ €
  Muschel und Seestern
  $2,50$ €
  Einsatz
  $1,00$ €
  Berechne den Erwartungswert.
  Der Gewinnplan soll so verändert werden, dass das Spiel fair wird. Dazu soll der Gewinn von „zweimal Muschel" verändert werden, während alles andere unverändert bleibt.
  Wie hoch muss der Gewinn für „zweimal Muschel" sein?
  [5 Pkte]
2. Die Vorderseite einer Tennishalle hat annähernd die Form einer Parabel.
  Sie lässt sich mit der Funktionsgleichung $y=a x^{2}+c$ beschreiben.
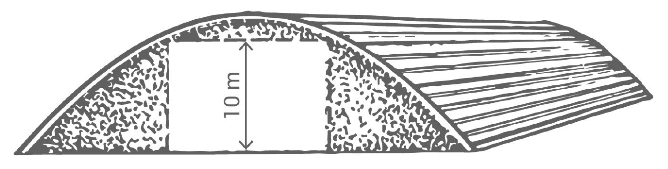
  Die maximale Höhe der Halle beträgt $12\m$ . Die Halle hat am Boden eine Breite von $40\m$ .
  Gib eine mögliche Funktionsgleichung an.
  In die Vorderseite der Tennishalle soll eine rechteckige Fensterfläche mittig eingebaut werden. Dazu werden zwei Vorschläge geprüft.
  Vorschlag 1:
  Die Fensterfläche soll eine Höhe von $10\m$ haben.
  Die beiden oberen Eckpunkte berühren den Parabelbogen (siehe Abbildung).
  Berechne den Flächeninhalt dieser Fensterfläche.
  Vorschlag 2:
  Die Fensterfläche soll eine Breite von $10\m$ haben.
  Berechne die größtmögliche Höhe dieser Fensterfläche.
  Welche der beiden Fensterflächen ist größer? Berechne.
  [5 Pkte]

Ereignis	Gewinn
zweimal Muschel	$9,00$ €
zweimal Seestern	$4,00$ €
Muschel und Seestern	$2,50$ €
Einsatz	$1,00$ €

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?