Auf der Oberfläche des quadratischen Prismas mit $a=3\text{ cm}$ und $h=2a$ liegt der Streckenzug $RSTUV$.

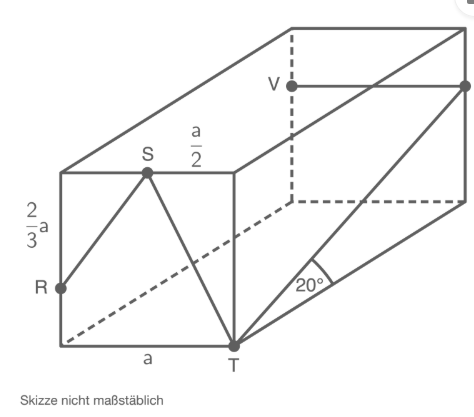
• Berechne die Länge des Streckenzuges $RSTUV$.

• Zeichne das Netz des Prismas und trage den Streckenzug ein.

Emil behauptet: „Wenn man die beiden Seitenlängen der Grundfläche des Prismas verdoppelt, verdoppelt sich auch das Volumen des Prismas."

• Nimm Stellung und begründe deine Entscheidung.

[5 Pkt]

Zu einer verschobenen, nach unten geöffneten Normalparabel gehört folgende Wertetabelle:

• Bestimme die Funktionsgleichung der Parabel.

• Vervollständige die Wertetabelle.

Till behauptet: „Jede nach unten geöffnete Normalparabel der Form $y=-x^2+c$ $(c\ne 0)$ besitzt nur negative $y$-Werte“. Hat Till Recht?

• Begründe deine Entscheidung durch Argumentation.

$(3x+6)\cdot (4-2x)=0$

• Löse die Gleichung.

[5 Pkt]