Nun wird die Funktion mit der Definitionsmenge betrachtet.
Ein Ausschnitt des Graphen von ist nebenstehend abgebildet.
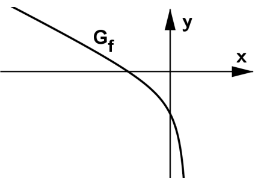
Die Funktion ist umkehrbar (Nachweis ist nicht erforderlich). Ermitteln Sie eine Gleichung der Umkehrfunktion von .
Zeigen Sie, dass gilt:
Der Graph von schließt zusammen mit den beiden Koordinatenachsen im
III. Quadranten des Koordinatensystems ein endliches Flächenstück ein.
Ermitteln Sie die Maßzahl des Flächeninhalts dieses Flächenstücks.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
