Teil 1 ohne Hilfsmittel Analysis

1
Gegeben ist die Funktion $f$ mit der Definitionsmenge $D_{f} = [- 1; + \infty [$ .
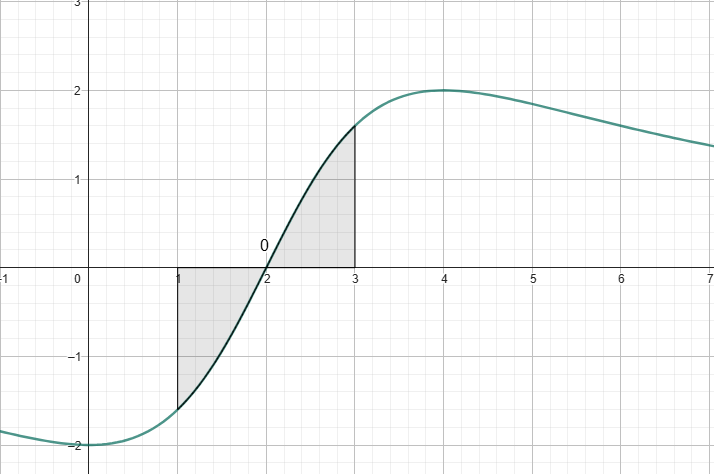
Der Graph von $f$ schneidet die x-Achse genau einmal, ist im Intervall $[4; + \infty [$ streng monoton fallend und wird mit $G_{f}$ bezeichnet. Ein Ausschnitt von $G_{f}$ ist in der nebenstehenden Abbildung zu sehen.
Betrachtet wird nun die Funktion
$F : x \mapsto \int_{1}^{x} f (t) d t$ mit der Definitionsmenge $D_{F} = [- 1; \infty [$ .
1. Geben Sie die Nullstellen von $F$ an. Runden Sie auf eine Nachkommastelle, sofern nötig. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
  Gib die Nullstellen von $F$ an
  Jede Integralfunktion hat eine Nullstelle an ihrer unteren Grenze $\Rightarrow x_{1} = 1$ .
  Die Funktion $f$ ist punktsymmetrisch zum Punkt $(2 | 0)$ . Demnach ist $| \int_{1}^{2} f (t) d t | = \int_{2}^{3} f (t) d t$ $\Rightarrow \int_{1}^{3} f (t) d t = 0$
  Die zweite Nullstelle von $F$ ist dann $x_{2} = 3$ .
  Die folgende Abbildung veranschaulicht den Sachverhalt.
  (Nicht in der Aufgabenstellung gefordert.)
  Flächenbilanz ist gleich null
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Jede Integralfunktion hat eine Nullstelle an ihrer unteren Grenze.
  Die Funktion $f$ ist punktsymmetrisch zum Punkt $(2 | 0)$ . Was folgt daraus für den Betrag des Intergrals $| \int_{1}^{2} f (t) d t |$ ?
2. Bestimmen Sie mithilfe des abgebildeten Graphen jeweils die x-Koordinate und die Art der Extrempunkte von $G_{F}$ . (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  Bestimme mithilfe des abgebildeten Graphen jeweils die x-Koordinate und die Art der Extrempunkte von $G_{F}$
  Es ist $F^{'} (x) = f (x)$ , sodass das Monotonieverhalten am gegebenen Funktionsgraphen abgelesen werden kann.
  $G_{f}$ verläuft für $- 1 \leq x < 2$ unterhalb der x-Achse und für $x > 2$ oberhalb.
  Bei $x = 2$ liegt eine Nullstelle von $f (x)$ vor. Der Graph von $G_{F}$ ist im Intervall $[- 1; 2]$ streng monoton fallend und im Intervall $[2; \infty [$ streng monoton steigend
  $\Rightarrow$ Tiefpunkt bei $x = 2$ und ein Randhochpunkt bei $x = - 1$ .
  Aus den dargestellten Eigenschaften folgt: bei $x = 2$ liegt der absolute Tiefpunkt von $G_{F}$ .
  Die folgende Abbildung veranschaulicht den Sachverhalt.
  (Nicht in der Aufgabenstellung gefordert.)
  Der grüne Graph gehört zur Funktion $f (x)$ .
  Der orangefarbige Graph gehört zu $f^{'} (x)$ .
  Der blaue Graph gehört zur Integralfunktion $F (x)$ .
  $G_{f}, G_{f^{'}}$ und $G_{F}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es ist $F^{'} (x) = f (x)$ , sodass das Monotonieverhalten am gegebenen Funktionsgraphen abgelesen werden kann.
3. Begründen Sie, ob folgende Aussage wahr oder falsch ist:
  „ $G_{F}$ ist im Intervall $[4; + \infty [$ rechtsgekrümmt.“ (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Krümmungsverhalten eines Funktionsgraphen
  Begründe, ob folgende Aussage wahr oder falsch ist: „ $G_{F}$ ist im Intervall $[4; + \infty [$ rechtsgekrümmt.“
  Es ist $F^{''} (x) = f^{'} (x)$ , sodass aus dem Monotonieverhalten von $G_{f}$ auf das Krümmungsverhalten von $G_{F}$ geschlossen werden kann.
  Gegeben: $G_{f}$ ist im Intervall $[4; + \infty [$ streng monoton fallend.
  In diesem Intervall ist $f^{'} (x) < 0$ und somit ist auch $F^{''} (x) < 0$ .
  Ist die zweite Ableitung kleiner null, dann ist $G_{F}$ in diesem Intervall rechtsgekrümmt. Die Aussage ist wahr.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es ist $F^{''} (x) = f^{'} (x)$ , sodass aus dem Monotonieverhalten von $G_{f}$ auf das Krümmungsverhalten von $G_{F}$ geschlossen werden kann.
2
Gegeben ist die streng monotone Funktion $g : x \mapsto \frac{2 e^{x}}{e^{x} + 4}$ mit der Definitionsmenge $D_{g} = ℝ$ .
Die Umkehrfunktion von $g$ wird $g^{- 1}$ bezeichnet.
1. Geben Sie die Wertemenge von $g^{- 1}$ an und ermitteln Sie die Definitionsmenge von $g^{- 1}$ , ohne dabei einen Funktionsterm von $g^{- 1}$ zu verwenden. (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge
  Gib die Wertemenge von $g^{- 1}$ an
  Gegeben ist $D_{g} = ℝ \Rightarrow W_{g^{- 1}} = ℝ$
  Die Wertemenge von $g^{- 1}$ ist $W_{g^{- 1}} = ℝ$ .
  Ermittle die Definitionsmenge von $g^{- 1}$ , ohne dabei einen Funktionsterm von $g^{- 1}$ zu verwenden
  Es gilt: $W_{g} = D_{g^{- 1}}$
  Ermittle also den Wertebereich der Funktion $g$ .
  Dabei ist $\lim_{x \to \infty} 2 \cdot \underset{\to 1}{\underset{⏟}{\frac{e^{x}}{e^{x} + 4}}} = 2$ .
  Weiterhin folgt: $\frac{e^{x} \cdot 2}{e^{x} \cdot (1 + 4 \cdot e^{- x})} = \frac{2}{1 + 4 \cdot e^{- x}}$
  Dann ist $\lim_{x \to - \infty} \frac{2}{1 + \underset{\to \infty}{\underset{⏟}{4 \cdot e^{- x}}}} = 0$
  Somit ist $W_{g} =] 0; 2 [= D_{g^{- 1}}$
  Die Definitionsmenge von $g^{- 1}$ ist $D_{g^{- 1}} =] 0; 2 [$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  $W_{g^{- 1}} = D_{g}$ . Bestimme also $D_{g}$ .
  Teil 2
  $D_{g^{- 1}} = W_{g}$ . Bestimme also $W_{g}$ . (Grenzwertbetrachtung)
2. Bestimmen Sie nun einen Funktionsterm von $g^{- 1}$ . (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Umkehrfunktion
  Bestimme einen Funktionsterm von $g^{- 1}$
  Gegeben ist $g : y = \frac{2 e^{x}}{e^{x} + 4}$ .
  Ersetze $x$ durch $y$ und löse nach $y$ auf.
  $x$ $=$ $\frac{2 e^{y}}{e^{y} + 4}$ $\cdot (e^{y} + 4)$
  ↓
  Löse nach $y$ auf.
  $x \cdot (e^{y} + 4)$ $=$ $2 e^{y}$
  ↓
  Löse die Klammer auf.
  $x \cdot e^{y} + 4 x$ $=$ $2 e^{y}$ $- x \cdot e^{y}$
  $4 x$ $=$ $2 e^{y} - x \cdot e^{y}$
  ↓
  Klammere $e^{y}$ aus.
  $4 x$ $=$ $e^{y} \cdot (2 - x)$ $: (2 - x)$
  $\frac{4 x}{2 - x}$ $=$ $e^{y}$ $\ln ()$
  $\ln (\frac{4 x}{2 - x})$ $=$ $y$
  Damit ist die Umkehrfunktion $g^{- 1} (x) = \ln (\frac{4 x}{2 - x})$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Ersetze $x$ durch $y$ und löse nach $y$ auf.
3. Die Funktion $G$ mit der Definitionsmenge $D_{G} = ℝ$ ist eine Stammfunktion von $g$ . Der Graph der Funktion $G$ schneidet die y-Achse bei $y_{0} = \ln (10)$ . Ermitteln Sie einen möglichen Term der Funktion $G$ . (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden
  Ermittle einen möglichen Term der Funktion $G$
  $\int \frac{2 e^{x}}{e^{x} + 4} d x = 2 \cdot \ln (| e^{x} + 4 |) + C \Rightarrow G (x) = 2 \cdot \ln (e^{x} + 4) + C$
  Der Graph der Funktion $G$ schneidet die y-Achse bei $y_{0} = \ln (10)$ .
  $\Rightarrow G (0) = \ln (10)$
  $2 \cdot \ln (e^{0} + 4) + C$ $=$ $\ln (10)$
  $2 \cdot \ln (1 + 4) + C$ $=$ $\ln (10)$
  $2 \cdot \ln (5) + C$ $=$ $\ln (10)$ $- 2 \cdot \ln (5)$
  $C$ $=$ $\ln (10) - 2 \cdot \ln (5)$
  ↓
  Wende Logarithmusgesetze an.
  $C$ $=$ $\ln (10) - \ln (5^{2})$
  $C$ $=$ $\ln (\frac{10}{5^{2}})$
  $C$ $=$ $\ln (0,4)$
  Damit ist die gesuchte Stammfunktion $G (x) = 2 \cdot \ln (e^{x} + 4) + \ln (0,4)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte, dass die Stammfunktion eine ln-Funktion ist.
  Bestimme die Integrationskonstante mit der Aussage "Der Graph der Funktion $G$ schneidet die y-Achse bei $y_{0} = \ln (10)$ ".

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$x$	$=$	$\frac{2 e^{y}}{e^{y} + 4}$	$\cdot (e^{y} + 4)$
	↓	Löse nach $y$ auf.
$x \cdot (e^{y} + 4)$	$=$	$2 e^{y}$
	↓	Löse die Klammer auf.
$x \cdot e^{y} + 4 x$	$=$	$2 e^{y}$	$- x \cdot e^{y}$
$4 x$	$=$	$2 e^{y} - x \cdot e^{y}$
	↓	Klammere $e^{y}$ aus.
$4 x$	$=$	$e^{y} \cdot (2 - x)$	$: (2 - x)$
$\frac{4 x}{2 - x}$	$=$	$e^{y}$	$\ln ()$
$\ln (\frac{4 x}{2 - x})$	$=$	$y$

$2 \cdot \ln (e^{0} + 4) + C$	$=$	$\ln (10)$
$2 \cdot \ln (1 + 4) + C$	$=$	$\ln (10)$
$2 \cdot \ln (5) + C$	$=$	$\ln (10)$	$- 2 \cdot \ln (5)$
$C$	$=$	$\ln (10) - 2 \cdot \ln (5)$
	↓	Wende Logarithmusgesetze an.
$C$	$=$	$\ln (10) - \ln (5^{2})$
$C$	$=$	$\ln (\frac{10}{5^{2}})$
$C$	$=$	$\ln (0,4)$

Teil 1 ohne Hilfsmittel Analysis

Gib die Nullstellen von F an

Hast du eine Frage oder Feedback?

Bestimme mithilfe des abgebildeten Graphen jeweils die x-Koordinate und die Art der Extrempunkte von GF

Hast du eine Frage oder Feedback?

Begründe, ob folgende Aussage wahr oder falsch ist: „GF ist im Intervall [4;+∞[ rechtsgekrümmt.“

Hast du eine Frage oder Feedback?

Gib die Wertemenge von g−1 an

Ermittle die Definitionsmenge von g−1, ohne dabei einen Funktionsterm von g−1 zu verwenden

Hast du eine Frage oder Feedback?

Bestimme einen Funktionsterm von g−1

Hast du eine Frage oder Feedback?

Ermittle einen möglichen Term der Funktion G

Hast du eine Frage oder Feedback?

Gib die Nullstellen von $F$ an

Bestimme mithilfe des abgebildeten Graphen jeweils die x-Koordinate und die Art der Extrempunkte von $G_{F}$

Begründe, ob folgende Aussage wahr oder falsch ist: „ $G_{F}$ ist im Intervall $[4; + \infty [$ rechtsgekrümmt.“

Gib die Wertemenge von $g^{- 1}$ an

Ermittle die Definitionsmenge von $g^{- 1}$ , ohne dabei einen Funktionsterm von $g^{- 1}$ zu verwenden

Bestimme einen Funktionsterm von $g^{- 1}$

Ermittle einen möglichen Term der Funktion $G$