1 Übersicht
Inhalt des Kurses
Das Prozentzeichen ist dir sicher schon im Alltag begegnet. Man findet es zum Beispiel in Einkaufszentren oder im Supermarkt. Allerdings wissen viele nicht, was genau damit gemeint ist und was das mit den Preisen zu tun hat. Das Ziel dieses Kurses ist, dass du anschließend mit dem Prozentzeichen umgehen kannst und die Grundprinzipien der Prozentrechnung verinnerlicht hast. Im Folgenden wird erklärt, was das Prozentzeichen bedeutet und wie Prozentzahlen, Dezimalzahlen und Bruchzahlen zusammenhängen.
Vorkenntnisse
Du solltest gut mit Bruchzahlen umgehen können.
Dazu gehört, dass du Brüche erweitern, kürzen und mit ihnen rechnen kannst. In dem Kurs Rechnen mit Brüchen erhältst du eine Einführung in die Bruchrechnung.
Du solltest gut mit Dezimalzahlen umgehen können. Der Kurs Überblick zu Dezimalbrüchen gibt dir einen Überblick über das Rechnen mit Dezimalzahlen und erklärt, wie man Dezimalzahlen in Brüche umwandelt.
Kursdauer
2 Stunden
2 Prozente aus dem Alltag
Das Prozentzeichen ist aus vielen Situationen bekannt. Häufig findet man es im Supermarkt, bei Wahlergebnissen, auf Lebensmitteln und bei vielem mehr. Bei einigen Prozentangaben weiß man sofort, was gemeint ist, wohingegen man sich zu anderen Prozentangaben weniger vorstellen kann.
In der Akkuanzeige eines Handys, eines Laptops oder einer Kamera
In Nährwerttabellen auf Lebensmittelverpackungen

Sportler sagen oft, sie würden in jedem Wettkampf geben.

Beim Elfmeterschießen berichten Fußballkommentatoren oft von sogenannten Trefferquoten. Ein guter Elfmeterschütze hat zum Beispiel eine Trefferquote von .

Die in der Akkuanzeige bedeuten offenbar, dass noch die Hälfte der Akkuleistung zur Verfügung steht. Man sagt dann oft "der Akku wäre noch halb voll".
"Die Hälfte" kannst du schon als Bruchzahl darstellen. und haben also die gleiche Bedeutung. Nun stellt sich die Frage, wie das mit komplizierteren Prozentangaben wie etwa oder ist.

3 Prozent - Eine neue Zahldarstellung
Wie eben gesehen entspricht also des Handy-Akkus genau der Hälfte und damit dem Bruch .
Dies kann man sich auch gut an einer Pizza veranschaulichen.
Wird eine Pizza halbiert, entspricht eine Hälfte genau der ganzen Pizza.
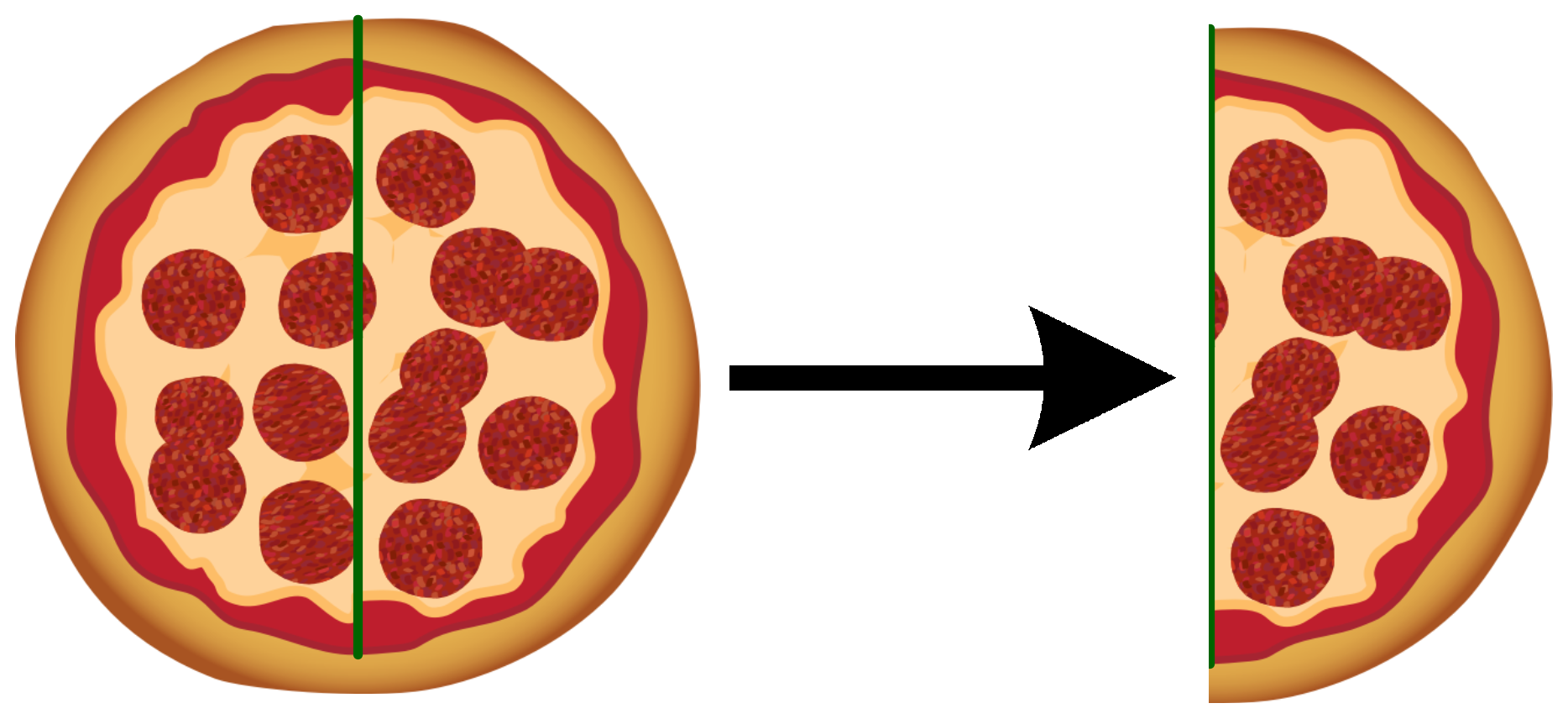
Ein Viertel der Pizza erhältst du bei einer weiteren Halbierung. Die Prozentzahl, die dem Viertel entspricht, erhältst du, wenn du auch die halbierst.
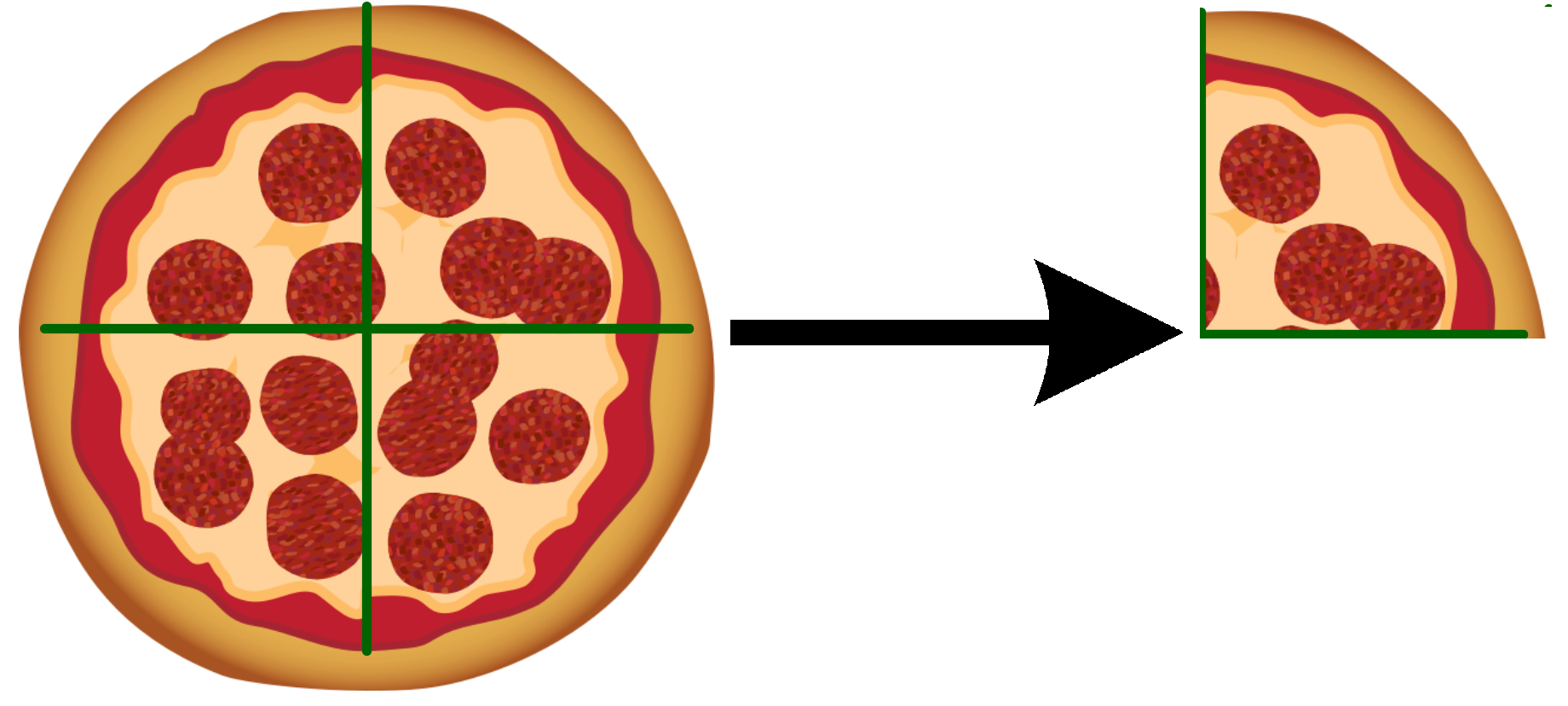
Werden nun die Viertel jeweils in 25 Stücke geteilt, entstehen insgesamt 100 Stücke, die jeweils ein Hundertstel von der ganzen Pizza ausmachen. Dementsprechend werden auch die durch 25 geteilt. Eine hundertstel Pizza entspricht somit .
Daraus lässt sich nun ableiten, dass
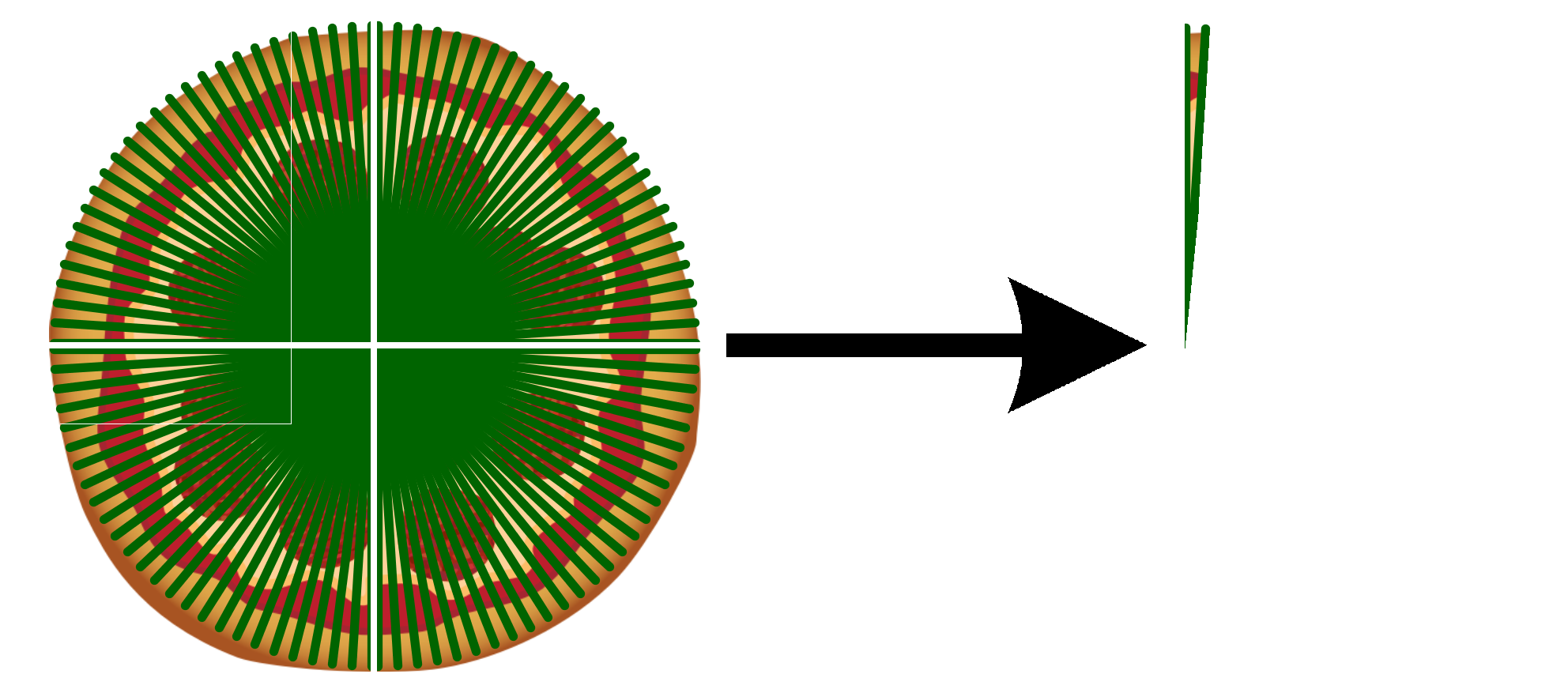
Formal schreibt man:
Laden
Orientiere dich bei folgender Aufgabe an dem Pizzabeispiel von oben:
Laden
4 Prozentzahlen über 100%
Bisher wurden nur solche Prozentzahlen betrachtet, die kleiner als waren. Was aber bedeuten zum Beispiel ?
Um das zu untersuchen, wenden wir die eben hergeleitete Formel auf an.
Also wählen wir .
Also:
Gekürzt sind das:
Wie vorher ist die Prozentzahl nichts anderes als eine weitere Darstellung für einen Bruch (nämlich ).
Auf das Pizzabeispiel übertragen, kann man sich fragen: Was sind von einer Pizza?
von einer Pizza sind das gleiche wie einer Pizza, also eineinviertel Pizzen.

Jede Prozentzahl kann somit als eine andere Darstellung für einen entsprechenden Bruch gesehen werden. Zwischen den beiden Darstellungsformen kann man mit der Formel hin und her wechseln, egal wie groß ist. Dabei wird die Prozentdarstellung im Normalfall vor allem dann verwendet, wenn man Größen vergleichen möchte.
5 Umformungen von Prozentzahlen und Dezimalzahlen
Bisher ist dir bekannt, dass . Jetzt erfährst du, wie Prozentangaben und Dezimalzahlen ineinander umgewandelt werden können.
Prozentzahl Dezimalzahl
Um eine Prozentzahl in eine Dezimalzahl umzurechnen, musst du die Zahl p durch 100 teilen.
Dezimalzahl Prozentzahl
Um eine Dezimalzahl d in eine Prozentzahl umzuwandeln, musst du die Dezimalzahl in einen Bruch mit dem Nenner 100 umrechnen. Dazu erweiterst du die Dezimalzahl mit 100.
Beispiele
Wenn du die 53 durch 100 teilst, erhältst du die gleichwertige Dezimalzahl.
Wenn du die 0,47 mit 100 multiplizierst, erhältst du die gleichwertige Prozentzahl.
Richtig mit dem Komma umgehen
Du weißt inzwischen, dass
Es ist so, dass das Komma bei der Prozentzahl immer zwei Stellen weiter rechts ist als bei der Dezimalzahl.
Prozentzahl in Dezimalzahl umrechnen | Dezimalzahl in Prozent umrechnen |
|---|---|
Man verschiebt das Komma um zwei Stellen nach links. | Man verschiebt das Komma um zwei Stellen nach rechts. |
6 Übungsaufgaben zur Umrechnung von Prozentzahlen und Dezimalzahlen
Laden
Laden
Laden
7 Umrechnungen von Prozentzahlen und Bruchzahlen
Im Folgenden erfährst du nun, wie Prozentangaben und Bruchzahlen ineinander umgewandelt werden können.
Bisher weißt du, dass die Prozentangabe die Anzahl der Hundertstel angibt.
Zum Beispiel gilt . Diesen Bruch musst du nur noch so weit wie möglich kürzen.
Um einen Bruch in eine Prozentzahl umzurechnen, machst du es genau umgekehrt: Du erweiterst den Bruch auf den Nenner 100. Dann entspricht der Zähler der Prozentzahl.
Es gibt aber auch Brüche, die sich nicht so leicht auf den Nenner 100 erweitern lassen. Solche Brüche wandelst du am besten in Dezimalzahlen um. Wenn du den Bruch als Dezimalzahl ausgedrückt hast, kannst du ihn so wie bereits gelernt in eine Prozentzahl umrechnen:
Merke:
8 Übungsaufgaben zur Umrechnung von Prozentzahlen und Bruchzahlen
Laden
Laden
9 Vorstellungen zu Prozenten und Brüchen
Es gibt verschiedene Möglichkeiten, wie du dir Brüche vorstellen kannst.
Bruch als einzelne Zahl | Bruch als Beschreibung eines Anteils |
|---|---|
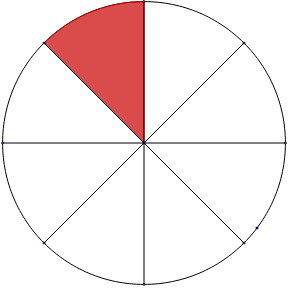
Ein Bruch für sich ist eine rationale Zahl, die man auch auf einem Zahlenstrahl wiederfindet. | Oft beschreiben Brüche aber auch Anteile. So sagt man zum Beispiel " von einer Pizza" oder " der Kinder einer Klasse". Hier bezieht sich der Bruch immer auf einen Grundwert (d.h. auf ein Ganzes, hier "die ganze Pizza" oder "alle Kinder einer Klasse"). |
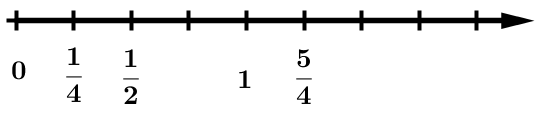 |  |
Ebenso hast du verschiedene Möglichkeiten dir Prozentangaben vorzustellen.
Prozent als Zahl | Prozent als Beschreibung eines Anteils |
|---|---|
Mit der Formel lässt sich jede Prozentzahl als Bruch umwandeln und lässt sich so auch auf einem Zahlenstrahl darstellten. | Fast immer beziehen sich Prozentzahlen auf etwas. Man sagt zum Beispiel " vom Akku" oder " Ballbesitz". Wie bei Brüchen beziehen sich die Prozentzahlen auch auf einen Grundwert ("voll geladener Akku" oder " Ballbesitz"). |
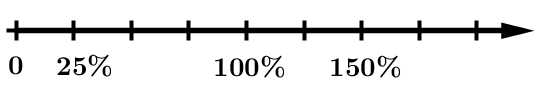 |  |
Die Darstellung von Prozenten am Zahlenstrahl ist sehr ungewöhnlich, soll dir aber zeigen, dass du Prozentzahlen genauso als Zahlen betrachten kannst wie Brüche. Die Zahlvorstellung brauchst du vor allem, wenn du mit Prozentzahlen rechnen willst. | Dass Prozente Anteile von etwas beschreiben, ist dir wahrscheinlich schon geläufig. Diese Vorstellung ist sehr wichtig, um Aufgaben zu verstehen und im täglichen Umgang mit Prozenten zurechtzukommen. |
Achtung: Mit dem Wort "Anteil" kann man auch meinen, dass die Prozentzahl etwas beschreibt, das größer als die Bezugsgröße ist (zum Beispiel sind " von einer Pizza" mehr als eine Pizza).
10 Grafische Veranschaulichung
Hier wird dir veranschaulicht welche Besonderheiten Prozentangaben mit sich bringen.
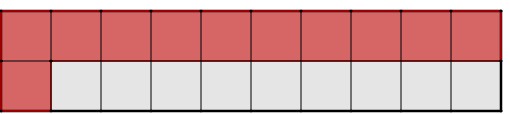
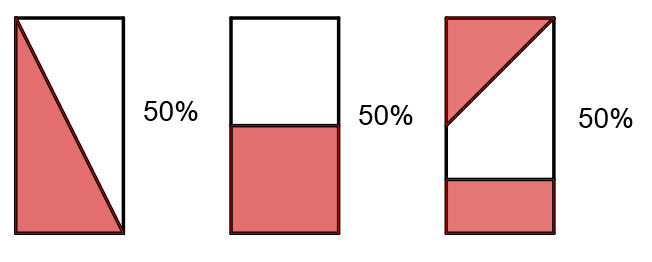
Hier haben alle rot eingezeichneten Flächen des Flächeninhalts des Rechtecks. Das Rechteck entspricht dann der Grundmenge. Man kann somit sehen, dass verschiedene Mengen die gleiche Prozentzahl haben können.
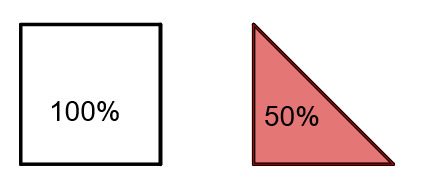
In diesem Beispiel wird eine Dreiecksfläche mit der Fläche eines Quadrats verglichen. Deshalb entspricht hier die gesamte Dreiecksfläche nur . Die Prozentzahl ist nämlich von der Bezugsgröße abhängig. Die Bezugsgröße kann auch ein anderes Objekt sein (hier die Fläche eines Quadrats).
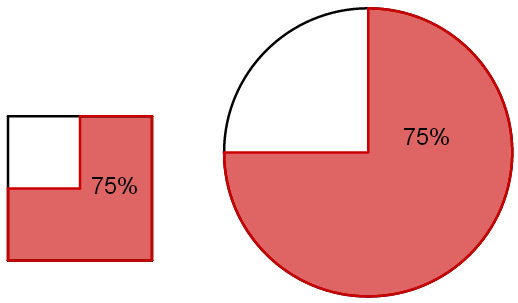
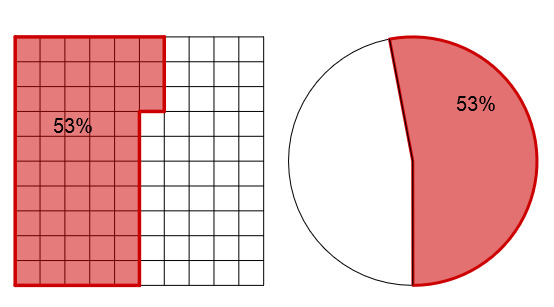
Hier sind die Prozentzahlen dieselben (jeweils ), sie beschreiben aber unterschiedlich große Flächen. Dies liegt daran, dass sich die Prozentzahlen auf unterschiedliche Grundwerte (hier die Quadratfläche und die Kreisfläche) beziehen können.

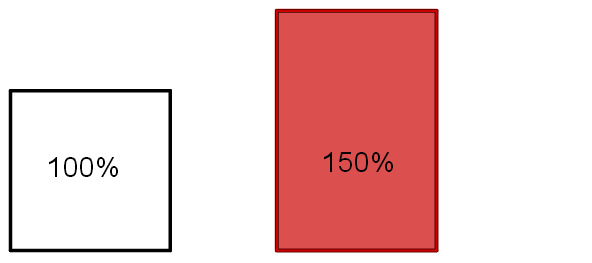
Prozentangaben können auch größer als sein. Dann werden nicht mehr kleinere, sondern größere Flächen mit deiner Ausgangsfläche verglichen.
Diagramme
Es gibt verschiedene Diagramme, mit denen man Prozentzahlen darstellen kann:
Mit dem Kästchen- und dem Kreisdiagramm stellt man meist Teilmengen eines Ganzen dar. Die Gesamtfläche entspricht dann dem Ganzen und der ausgefüllte Teil dem Anteil der Teilmenge.
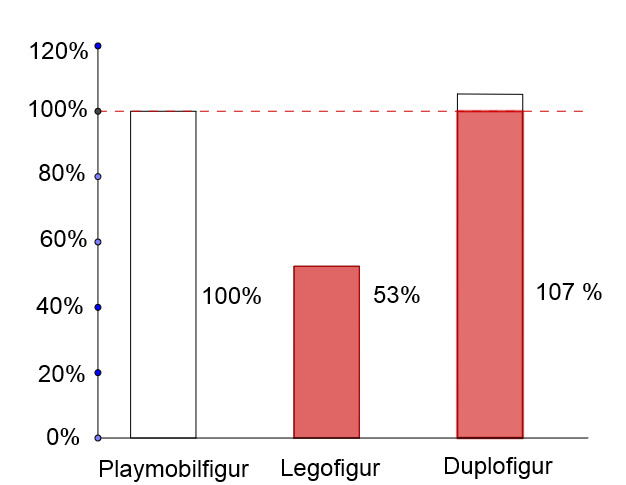
Will man auch einen Zuwachs beschreiben können (z.B. deine jetzige Größe im Vergleich zu deiner Größe in einem Jahr) oder einfach Mengen, die größer sind als unsere Ausgangsmenge, so wählt man am besten ein Säulendiagramm.
Hier sieht man einen Größenvergleich zwischen jeweils einer Playmobil-, Lego- und Duplofigur als Säulendiagramm. Dabei wurde die Größe der Playmobilfigur als gewählt. Die beiden anderen Figuren werden damit verglichen.

11 Grafische Veranschaulichung - Übungsaufgaben
Gib die gefärbte Fläche in Prozent-, Dezimal- und Bruchschreibweise an!
Laden
Laden
Laden
Laden
12 Zusammenfassung
Allgemein gilt:
Mit Prozentzahlen können wir das Verhältnis einer Menge zu einer Grundmenge ausdrücken.
Das funktioniert mit Mengen, die kleiner sind als die Grundmenge, aber auch mit Mengen, die größer sind als die Grundmenge.
Prozentzahlen Dezimalzahlen
Um Dezimalzahlen in Prozentzahlen umzuwandeln, multiplizierst du die Dezimalzahl mit 100 oder verschiebst das Komma um zwei Stellen nach rechts.
Um Prozentzahlen in Dezimalzahlen umzuwandeln, dividierst du die Prozentzahl durch 100 oder verschiebst das Komma um zwei Stellen nach links.
Prozentzahlen Bruchzahlen
Um Bruchzahlen in Prozentzahlen umzuwandeln, erweiterst du den Bruch auf Hundertstel. Wenn das nicht funktioniert, wandelst du die Bruchzahl in eine Dezimalzahl um und gehst so vor wie oben.
Um Prozentzahlen in Bruchzahlen umzuwandeln, schreibst du die Prozentzahl als Hundertstelbruch und kürzt so weit wie möglich.
Jede Zahl hat also drei verschiedene Darstellungsformen.
13 Zeig, was du kannst!
Gib die gefärbte Fläche in Prozent-, Dezimal- und Bruchschreibweise an!
Laden
Laden
Laden
Laden
Hier findest du weitere Aufgaben zum Prozentzeichen und seiner Darstellung.
