Die freie Lernplattform

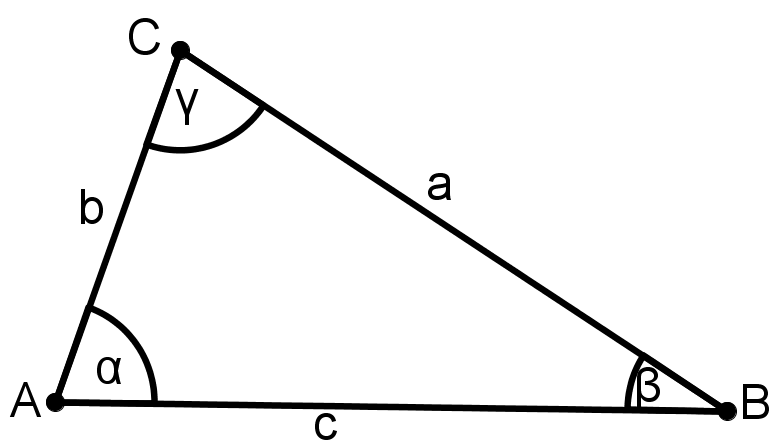
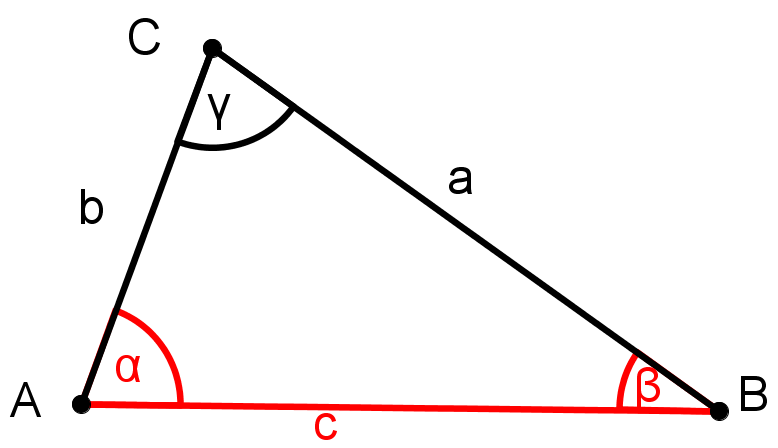
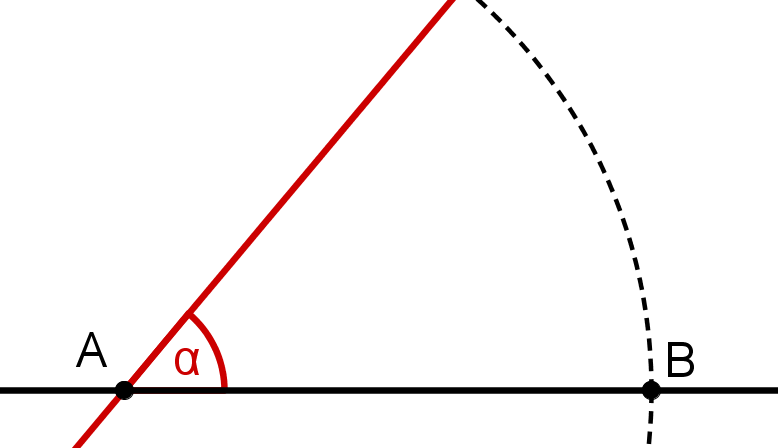
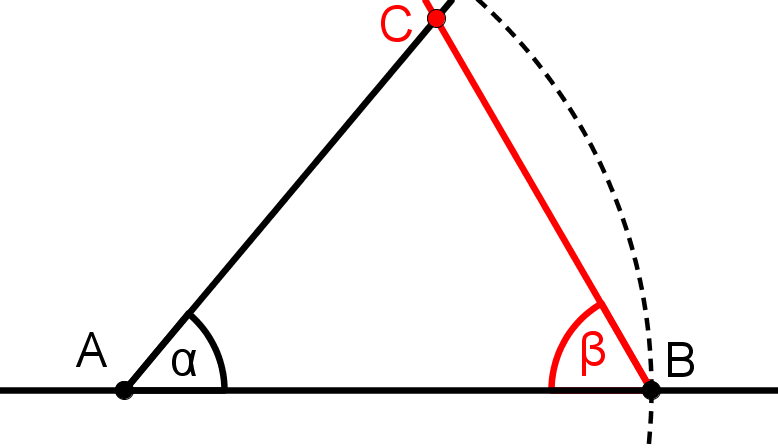
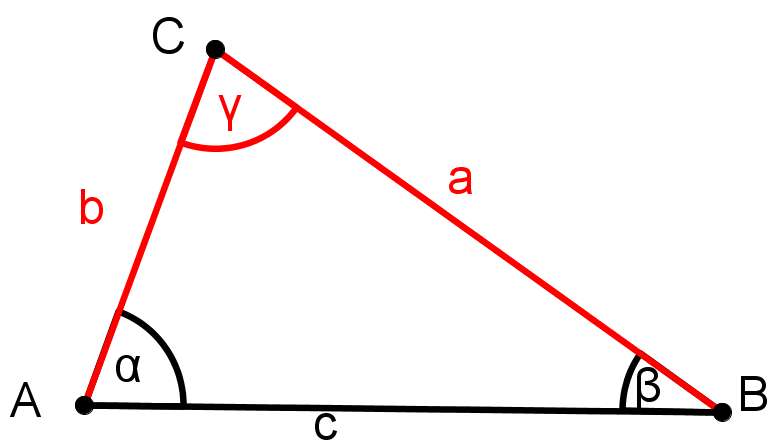
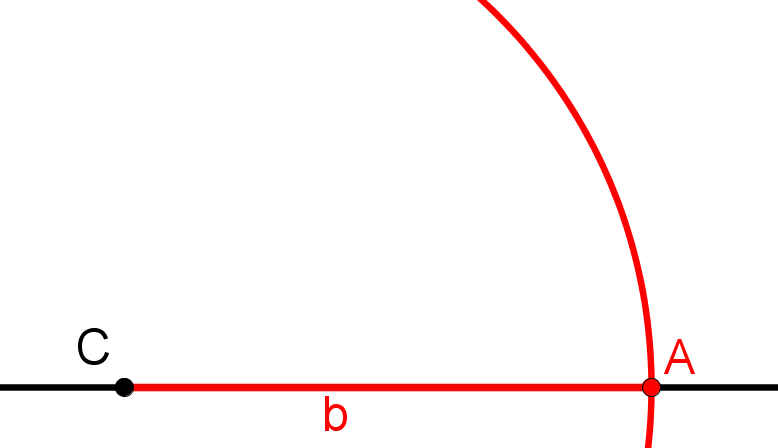
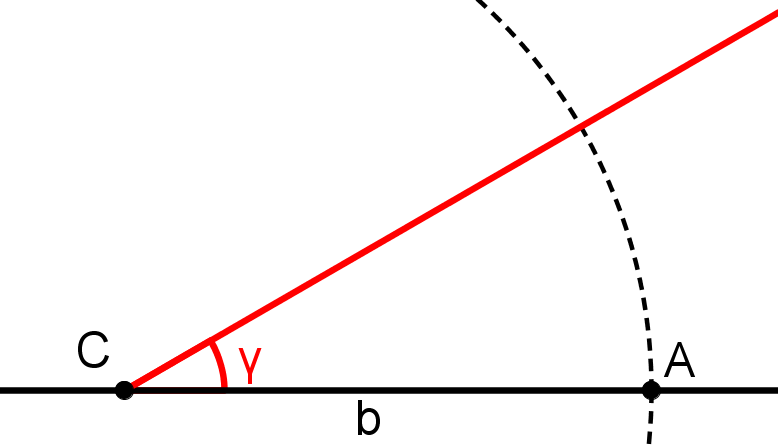
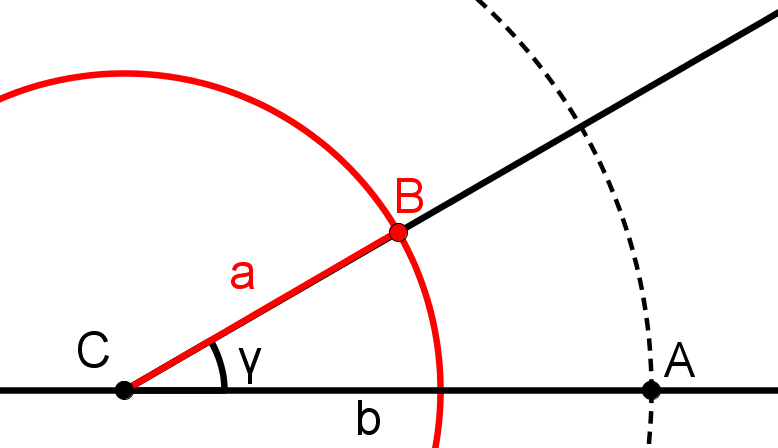
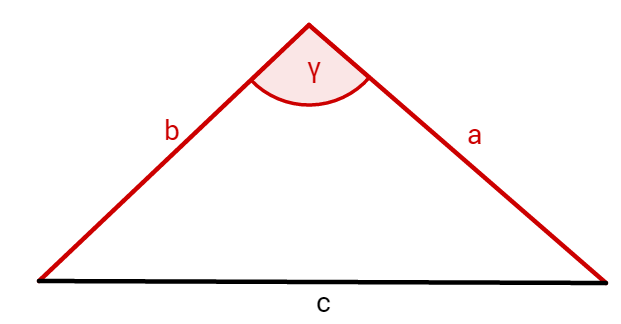
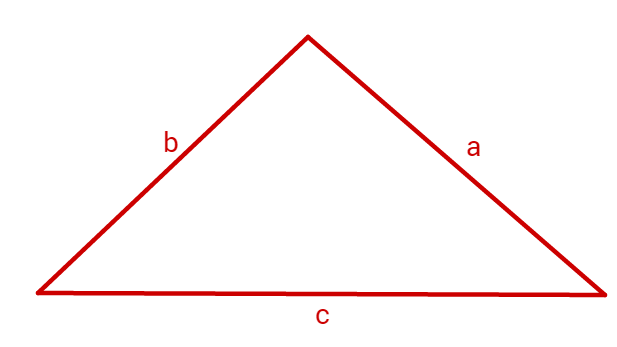
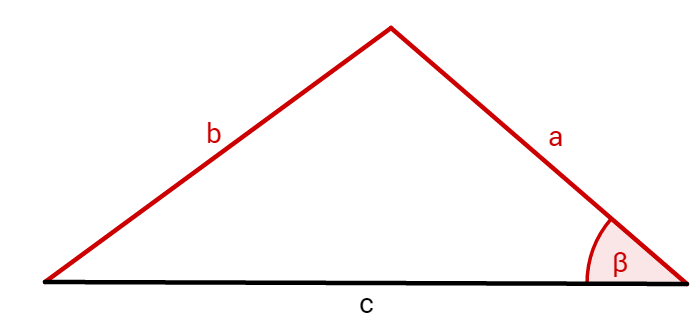
Aufgaben zur Konstruktion von Dreiecken

1
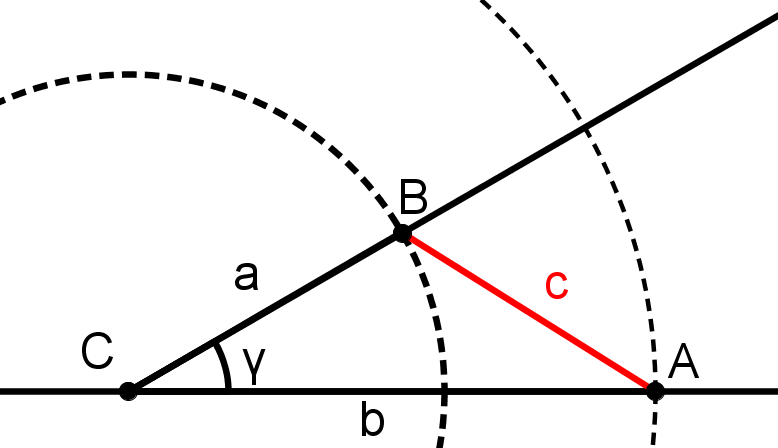
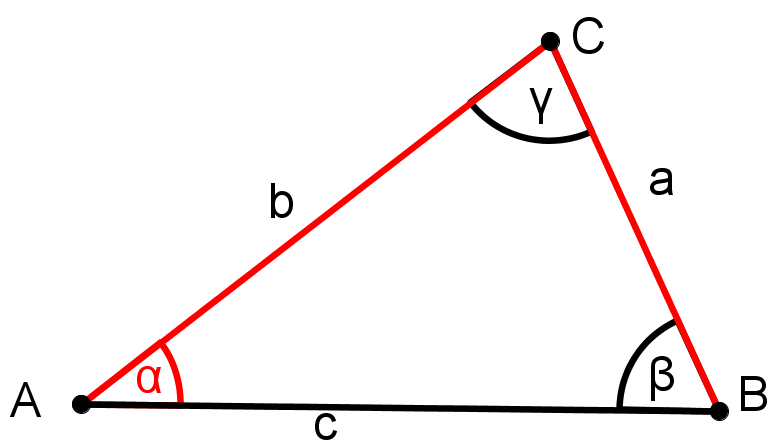
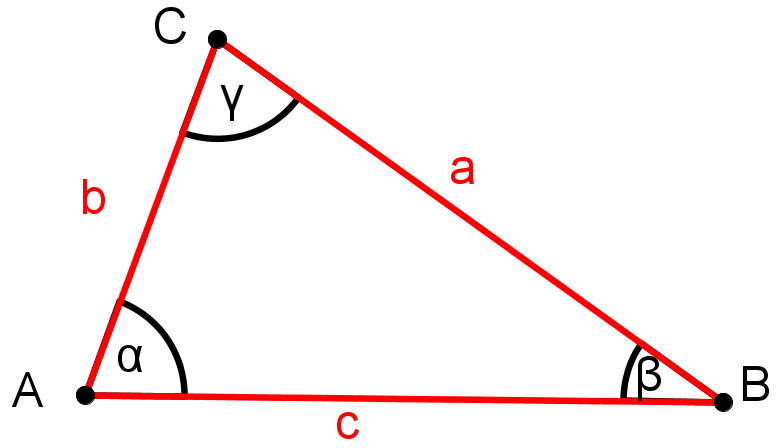
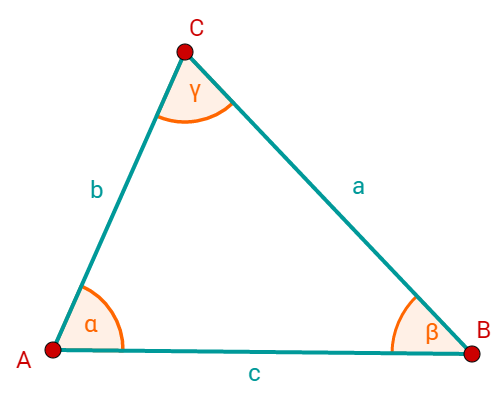
Entscheide, ob man aus folgenden Angaben eindeutig Dreiecke konstruieren kann.
Und wenn ja, konstruiere das Dreieck.
1. $c=5\;cm\;;\;\alpha=50^\circ\;;\;\beta=60^\circ$
  Das Dreieck ist eindeutig konstruierbar.
  Das Dreieck ist nicht eindeutig konstruierbar.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Dreiecken
  Skizze anfertigen
  Benenne ein beliebiges Dreieck
  Markiere die bekannten Größen. Man sieht in der Skizze, dass das Dreieck die Voraussetzung des WSW-Satzes erfüllt. Deshalb ist es eindeutig konstruierbar.
  Dreieck konstruieren
  Hier findest du das Applet zur Konstruktion mithilfe des WSW-Satzes.
  Zeichne eine Gerade und auf ihr irgendwo den Punkt A ein.
  Zeichne einen Kreis um A, dessen Radius genauso groß ist wie die Länge der Seite c.
  Der Schnittpunkt des Kreises mit der Geraden ist der Punkt B.
  Zeichne an A einen 50° Winkel.
  Zeichne an B einen 60° Winkel.
  Der Schnittpunkt der beiden Schenkel ist der Punkt C des Dreiecks.
  Somit hat man das Dreieck eindeutig konstruiert.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $a=3cm\;;\;b=5cm;\;\;\gamma=30^\circ$
  Das Dreieck ist eindeutig konstruierbar.
  Das Dreieck ist nicht eindeutig konstruierbar.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Dreiecken
  Skizze anfertigen
  Benenne ein beliebiges Dreieck
  Markiere die bekannten Größen.
  Man sieht in der Skizze, dass das Dreieck die Voraussetzung des SWS-Satzes erfüllt.
  Deshalb ist es eindeutig konstruierbar.
  Dreieck konstruieren
  Hier findest du ein Applet zur Konstruktion mithilfe des SWS-Satzes.
  Zeichne eine Gerade und auf ihr irgendwo den Punkt C ein.
  Zeichne einen Kreis um C, dessen Radius genauso groß ist wie die Länge der Seite b.
  Der Schnittpunkt des Kreises mit der Geraden ist der Punkt A.
  Konstruiere an C einen 30° Winkel .
  Zeichne um C einen Kreis, dessen Radius so groß ist wie die Seite a.
  Der Schnittpunkt des Kreises mit dem eben konstruierten Schenkel ist der Punkt B.
  Verbinde die Punkte A und B. Diese Strecke ist die Seite c.
  Das Dreieck ABC ist das gesuchte Dreieck.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $a=5\text{cm}\;;\;b=4\text{cm}\;;\;\;\alpha=45^\circ$
  Das Dreieck ist eindeutig konstruierbar.
  Das Dreieck ist nicht eindeutig konstruierbar.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Dreiecken
  Skizze anfertigen
  Benenne ein beliebiges Dreieck und markiere die bekannten Größen.
  Laut Skizze kommt nur der SsW-Satz in Frage. Es muss also noch überprüft werden, ob die Seite, die dem gegebenen Winkel gegenüberliegt größer ist als die andere Seite.
  Laut Angabe ist $a>b$ , weshalb die Voraussetzung des SsW-Satzes erfüllt ist.
  Deshalb ist es eindeutig konstruierbar.
  (VORSICHT: Würde man nur die Skizze betrachten, wäre $a<b$ )
  Dreieck konstruieren
  Hier findest du ein Applet zur Konstruktion mithilfe des SsW-Satzes.
  Zeichne einen Strahl von einem Punkt $A$ aus und konstruiere einen Winkel von $45^\circ$ mit dem Scheitel bei $A$ .
  Der Punkt $C$ liegt auf dem zweiten Schenkel des Winkels $4$ cm von $A$ entfernt.
  Zeichne einen Kreis um $C$ mit dem Radius $5$ cm. Der Schnittpunkt dieses Kreises mit dem Strahl von $A$ aus ist der Punkt $B.$
  Die Strecke AB ist die Seite c.
  Verbinde den Punkt $B$ mit dem Punkt $C$ . Diese Strecke ist die Seite $a$ .
  Das Dreieck $ABC$ ist das gesuchte Dreieck
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $a=3cm\;;\;b=4cm\;;\;c=8cm$
  Das Dreieck ist eindeutig konstruierbar.
  Das Dreieck ist nicht eindeutig konstruierbar.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Dreiecken
  Skizze anfertigen
  Benenne ein beliebiges Dreieck
  Markiere die bekannten Größen.
  Man sieht in der Skizze, dass das Dreieck die Voraussetzung des SSS-Satzes erfüllt.
  Deshalb wäre es eindeutig konstruierbar.
  ABER:
  Artikel zum Thema
  Dreiecksungleichung überprüfen
  $a = 3cm$
  $b = 4cm$
  $a + b = 3cm + 4cm = 7cm$
  aber:
  $c=8cm$
  $\rightarrow c>a+b$
  Da die Seite c größer als die Summe der anderen beiden Seiten ist, existiert dieses Dreieck nicht!
  Versucht man das Dreieck dennoch zu konstruieren (ohne die Dreiecksungleichung beachtet zu haben), stellt man fest, dass sich die Kreise die den Seiten a und b entsprechen nicht schneiden, es also kein Punkt C gibt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Die zwei Freundinnen Julia und Lena fahren sehr gerne Skateboard. Julias Papa hat Julia eine Rampe gebaut und jetzt will Lena auch so eine!
Die beiden telefonieren miteinander und Julia erklärt Lena, wie die Rampe aussieht:
"Die Rampe besteht aus einem Brett, das $2\;m$ lang ist und das andere ist $1{,}50\;m$ lang. Das $2\;m$ -Brett ist vorne, so dass du dann über das $1{,}5\;m$ Brett runter fährst."
Lena zeichnet sich gleich eine Skizze und baut die Rampe:
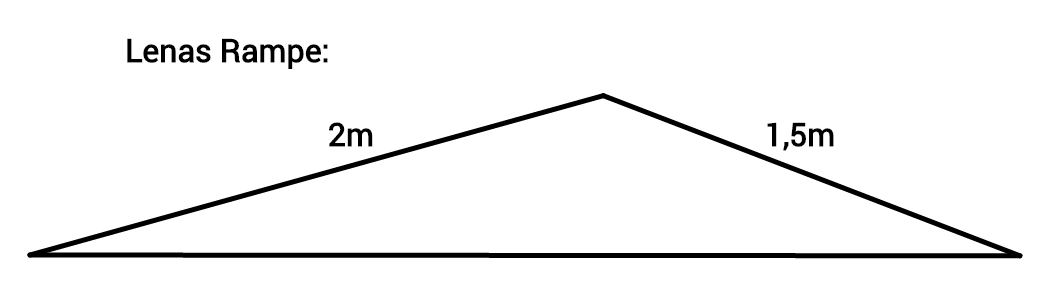
Zwei Wochen später telefonieren die beiden nochmal:
Lena sagt: "Die Rampe ist langweilig! Sie ist überhaupt nicht steil genug!"
Julia: "Meine nicht, sie ist sogar so steil, dass man nur mit viel Anlauf drüber kommt!"
Sie mailen sich die Bilder der Rampen zu, um sie zu vergleichen:
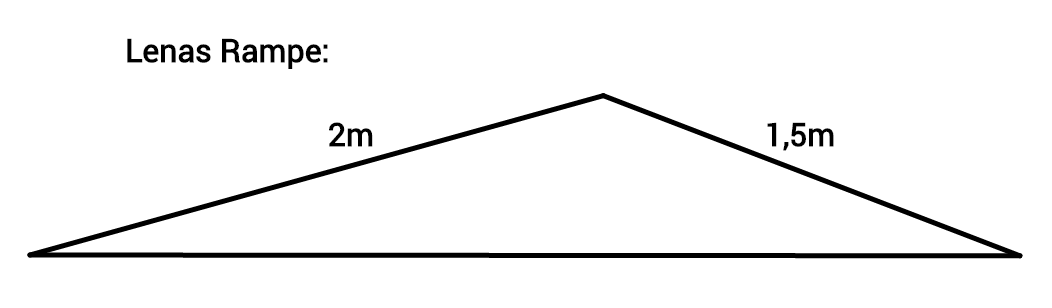
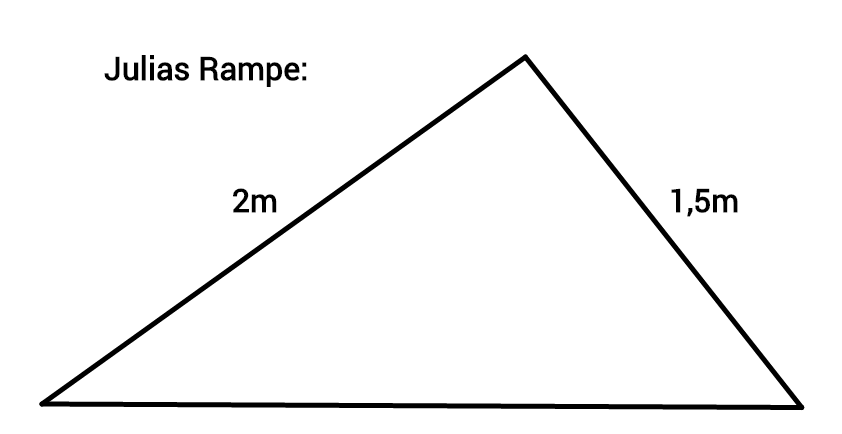
1. Warum sehen die beiden Rampen unterschiedlich aus?
  
  Uneindeutigkeit der Angaben
  Julia hat versucht, die Rampe nur mithilfe von zwei Angaben zu beschreiben. Die Rampe hat die Grundfläche eines Dreiecks, so dass man dieselben Kriterien für die Eindeutigkeit wie bei einem Dreieck annehmen kann.
  Ein Dreieck ist durch zwei Angaben nicht eindeutig beschrieben und somit nicht konstruierbar. Lena hat diese zwei Strecken-Angaben in einem anderen Winkel zusammengebaut als Julia und somit eine andere Rampe erhalten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Welche weitere Angabe könnte Julia an Lena weitergeben, so dass sie die Rampe identisch nachbauen kann?
  
  Eindeutigkeit der Rampe
  Die Rampe hat die Grundfläche eines Dreiecks. Dieses muss eindeutig sein.
  Dreiecke sind eindeutig, wenn ein Kongruenzsatz gegeben ist.
  In diesem Fall hast du zwei Strecken bereits gegeben, du suchst also einen Kongruenzsatz mit zwei Strecken und kannst dann die dritte Angabe hinzufügen.
  Mögliche Kongruenzsätze:
  SWS
  SsW
  SSS
  Überlege dir, welche Angabe Julia nun noch für die verschiedenen Kongruenzsätze ausmessen sollte.
  Gehe davon aus, dass die Strecke mit $2 \; m$ die Strecke $b$ ist und die Strecke $a=1{,}50 \; m$ .
  Für den SWS Satz wird der Winkel $\gamma$ benötigt.
  Für den SSS Satz wird die dritte Seite $c$ benötigt.
  Für den SsW-Satz wird der Winkel $\beta$ benötigt.
  Julia kann also eine der folgenden Angaben ausmessen:
  den Winkel $\gamma$ ,
  die Strecke $c$ ,
  den Winkel $\beta$
  Durch jede dieser drei Angaben wird das Dreieck eindeutig zu konstruieren und ist somit ausreichend beschrieben.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.