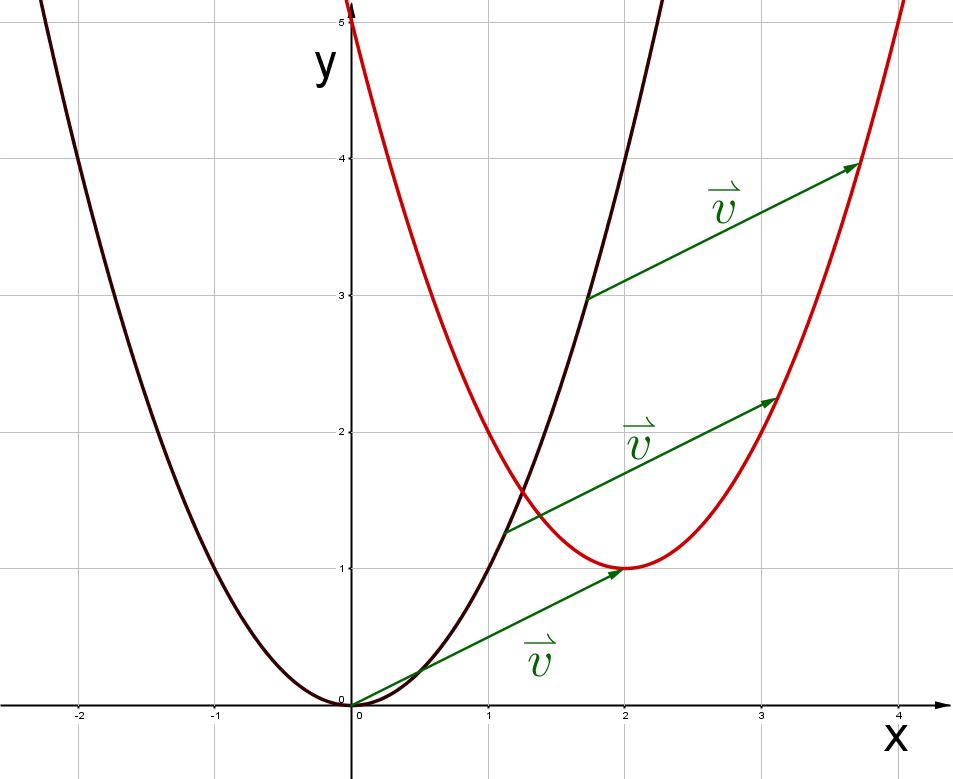
Verschiebe die Funktion um den Vektor .
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung
Um bei einer Funktion eine Parallelverschiebung um den Vektor durchzuführen, setzt du .
Alternative 1: Berechnung in Koordinatenform:
Setze in das Gleichungssystem ein.
Setze die Koordinaten des Vektors in das Gleichungssystem ein.
Ersetze in der Gleichung für .
Dies ist die Funktionsgleichung der verschobenen Funktion.
Alternative 2: Berechnung in Matrixform:
↓ Setze in den Vektor ein.
↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ Setze die Koordinaten des Vektors in den Vektor ein.
Ersetze in der Gleichung für .
Dies ist die Funktionsgleichung der verschobenen Funktion.
Hast du eine Frage oder Feedback?
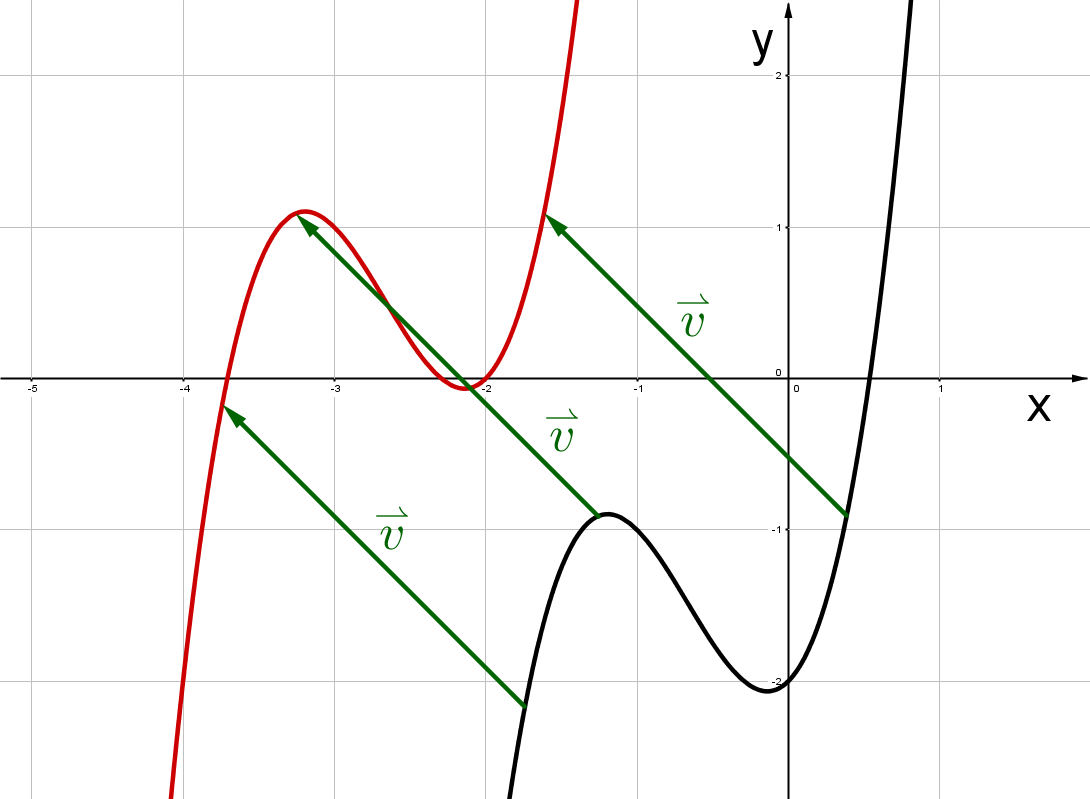
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung
Um bei einer Funtion eine Parallelverschiebung um einen Vektor zu durchzuführen, setzt du .
Alternative 1: Berechnung in Koordinatenform:
Setze in das Gleichungssystem ein.
Setze die Koordinaten des Vektors in das Gleichungssystem ein.
Setze die Gleichung für in die Gleichung für ein und vereinfache.
Dies ist die Funktionsgleichung der verschobenen Funktion.
Alternative 2: Berechnung in Matrixform:
↓ Setze in den Vektor ein.
↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ Setze die Koordinaten des Vektors in den Vektor ein.
Setze die Gleichung für in die Gleichung für ein.
Dies ist die Funktionsgleichung der verschobenen Funktion.
Hast du eine Frage oder Feedback?
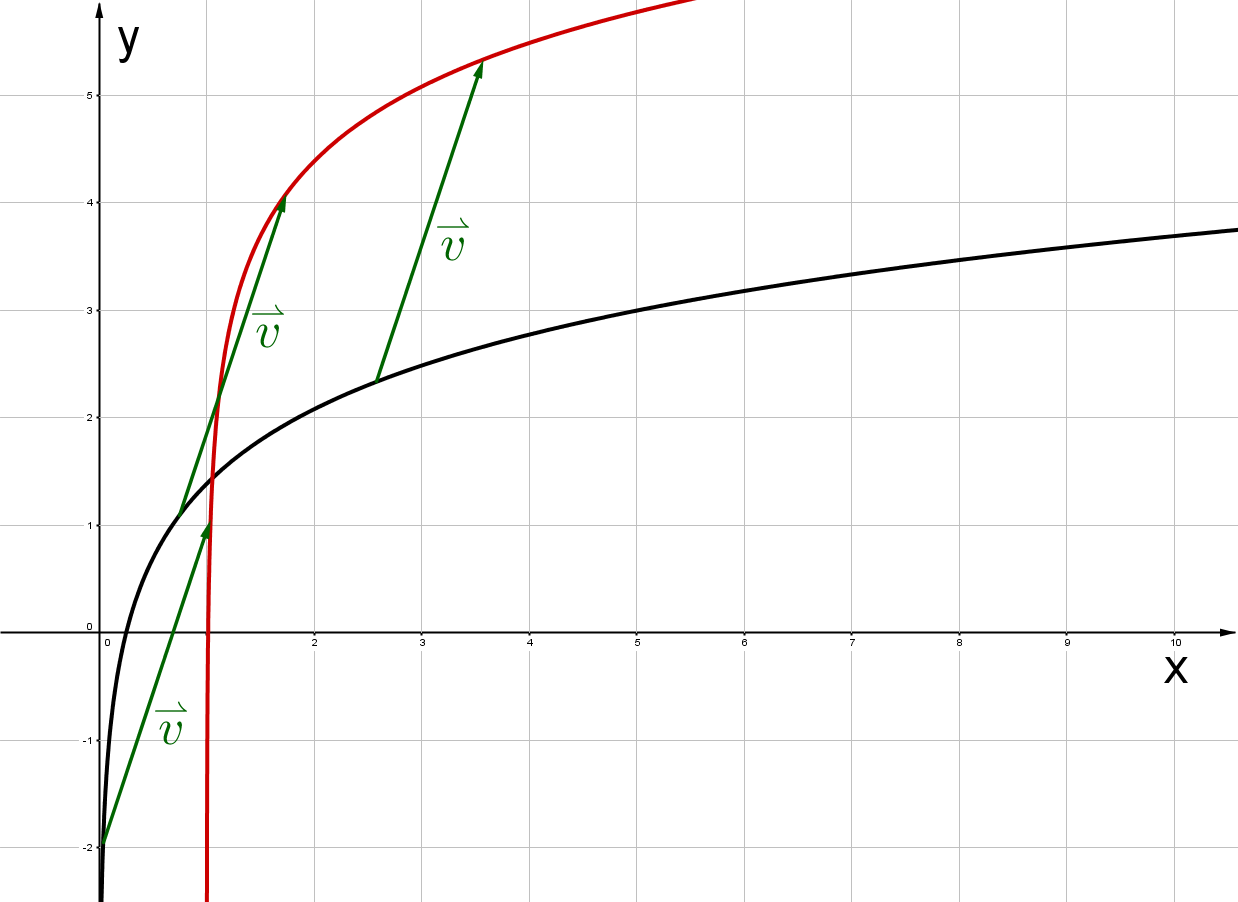
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung
Um bei einer Funktion eine Parallelverschiebung um den Vektor durchzuführen, setzt du .
Alternative 1: Berechnung in Koordinatenform:
Setze in das Gleichungssystem ein.
Setze die Koordinaten des Vektors in das Gleichungssystem ein.
Ersetze in der Gleichung für .
Dies ist die Funktionsgleichung der verschobenen Funktion.
Alternative 2: Berechnung in Matrixform:
↓ Setze in den Vektor ein.
↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ Setze die Koordinaten des Vektors in den Vektor ein.
Ersetze in der Gleichung für .
Dies ist die Funktionsgleichung der verschobenen Funktion.
Hast du eine Frage oder Feedback?
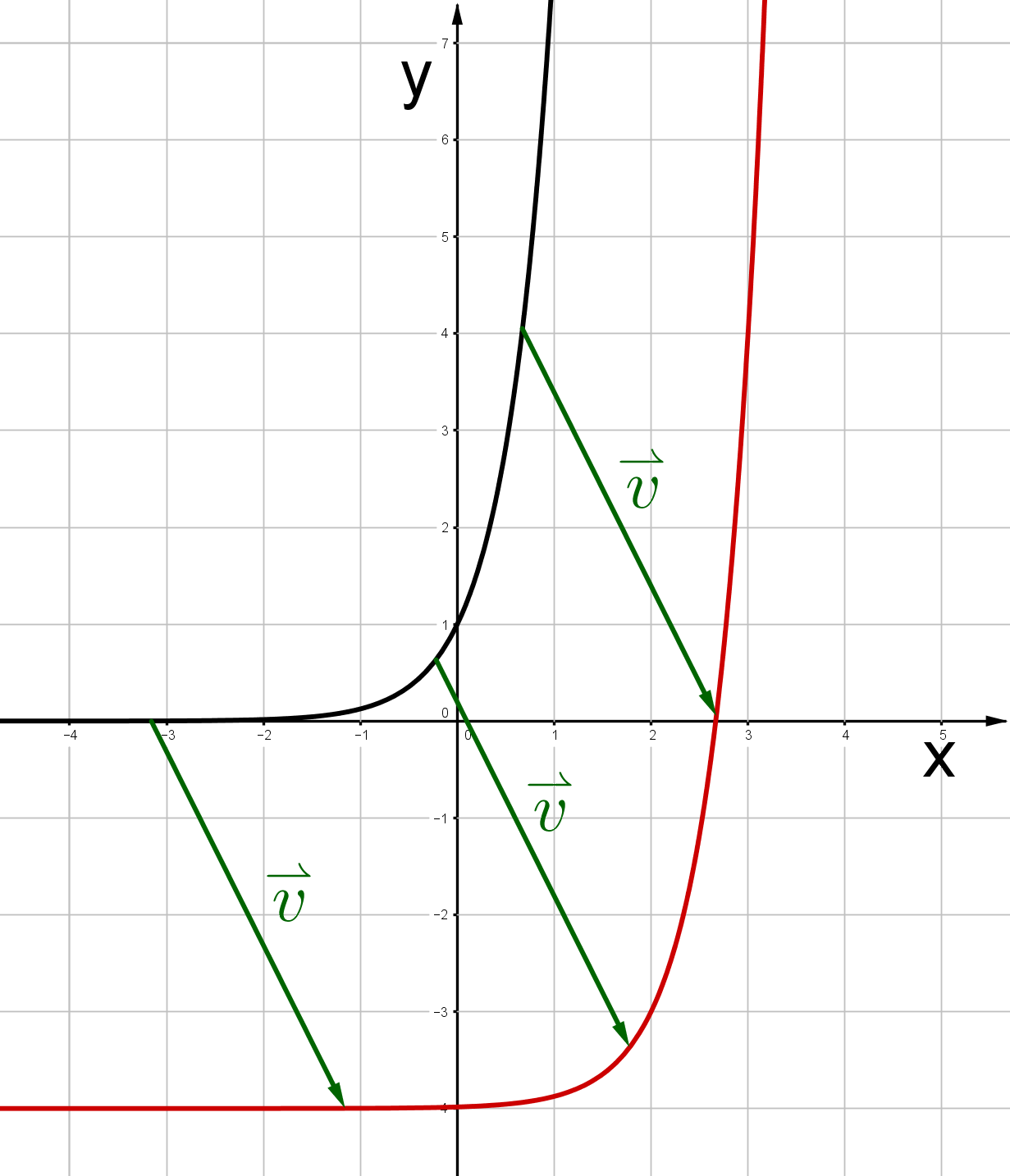
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung
Um bei einer Funktion eine Parallelverschiebung um den Vektor durchzuführen, setzt du .
Alternative 1: Berechnung in Koordinatenform:
Setze in das Gleichungssystem ein.
Setze die Koordinaten des Vektors in das Gleichungssystem ein.
Ersetze in der Gleichung für .
Dies ist die Funktionsgleichung der verschobenen Funktion.
Alternative 2: Berechnung in Matrixform:
↓ Setze in den Vektor ein.
↓ Führe die Matrix-Vektor-Multiplikation durch.
↓ Setze die Koordinaten des Vektors in den Vektor ein.
Ersetze in der Gleichung für .
Dies ist die Funktionsgleichung der verschobenen Funktion.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
