Übungsaufgaben zu trigonometrischen Funktionen

Überarbeiten
Teilen

Berechne alle Winkel $α$ zwischen $0 °$ und $360 °$ , die folgende Gleichung erfüllen:

[4 \cdot \sin (2 \cdot α) - (\sqrt{6} + \sqrt{2})] \cdot [{(\tan (\frac{α}{3}))}^{2} + 2 \cdot \sqrt{5} - 5] = 0

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrische Umkehrfunktion

[4 \cdot \sin (2 \cdot α) - (\sqrt{6} + \sqrt{2})] \cdot [{(\tan (\frac{α}{3}))}^{2} + 2 \cdot \sqrt{5} - 5] = 0

Die Gleichung ist $0$ , wenn einer der beiden Faktoren $0$ ist.

$[4 \cdot \sin (2 \cdot α) - (\sqrt{6} + \sqrt{2})] = 0$ oder $[{(\tan (\frac{α}{3}))}^{2} + 2 \cdot \sqrt{5} - 5] = 0$

Betrachte zunächst den ersten Faktor:

\begin{array}{rcll} 4 \cdot \sin (2 \cdot α) - (\sqrt{6} + \sqrt{2}) & = & 0 & | + (\sqrt{6} + \sqrt{2}) \\ 4 \cdot \sin (2 \cdot α) & = & \sqrt{6} + \sqrt{2} & | \div 4 \\ \sin (2 \cdot α) & = & \frac{\sqrt{6} + \sqrt{2}}{4} & | \sin^{- 1} (\dots) \\ 2 \cdot α & = & \sin^{- 1} (\frac{\sqrt{6} + \sqrt{2}}{4}) & | \div 2 \\ α & = & \frac{\sin^{- 1} (\frac{\sqrt{6} + \sqrt{2}}{4})}{2} \end{array}

Die rechte Seite der Gleichung kannst du nun mit dem Taschenrechner berechnen.

α = 37,5 °

Überprüfe nun, ob außer $α = 37,5 °$ noch weitere Winkel eine Lösung sein können. Betrachte dazu zum Beispiel den Einheitskreis:

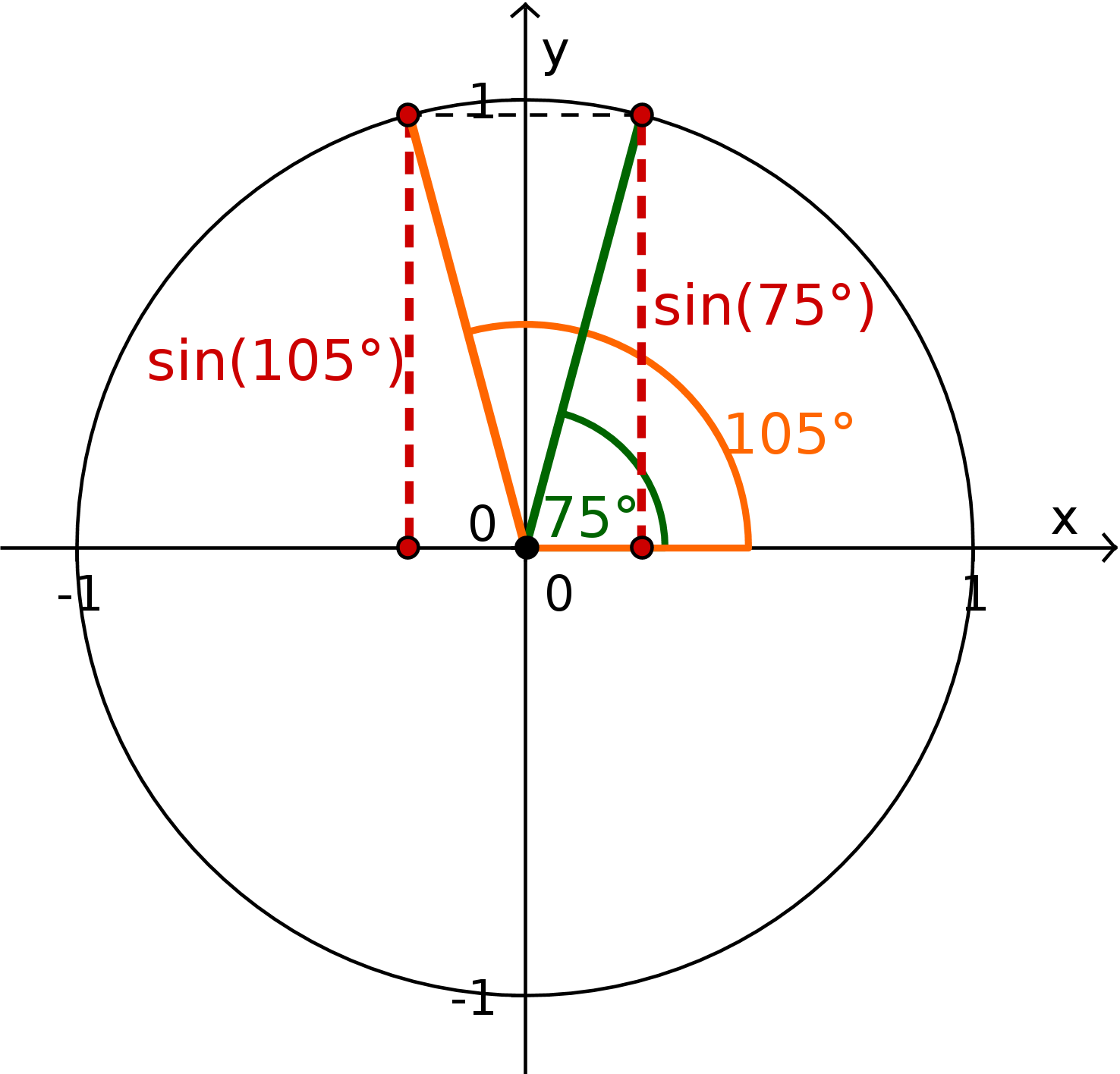
trigonometrische Funktionen Einheitskreis

Hier kannst du sehen, dass der Sinus für zwei Winkel den gleichen Wert annimmt. $\sin (75 °) = \sin (180 ° - 75 °) = \sin (105 °)$ . Daraus folgt $2 α = 105 °$ . Das heißt, $α = 52,5 °$ ist eine weitere Lösung.

Betrachte als nächstes den zweiten Faktor.

\begin{array}{rclll} {(\tan (\frac{α}{3}))}^{2} + 2 \cdot \sqrt{5} - 5 & = & 0 | - 2 \cdot \sqrt{5} | + 5 \\ {(\tan (\frac{α}{3}))}^{2} & = & - 2 \cdot \sqrt{5} + 5 & | \sqrt{} \\ \tan (\frac{α}{3}) & = & \pm \sqrt{- 2 \cdot \sqrt{5} + 5} & | \tan^{- 1} (\dots) \\ \frac{α}{3} & = & \tan^{- 1} (\pm \sqrt{- 2 \cdot \sqrt{5} + 5}) & | \cdot 3 \\ α & = & 3 \cdot \tan^{- 1} (\pm \sqrt{- 2 \cdot \sqrt{5} + 5}) \end{array}

Die rechte Seite der Gleichung kannst du nun mit dem Taschenrechner berechnen.

α = \pm 108 °

Gesucht sind Winkel zwischen $0 °$ und $360 °$ . Also ist $- 108 °$ keine gültige Lösung.

α = 108 °

Beachte: Für den Tangens gilt die Supplementbeziehung

\tan (\frac{α}{3}) = \tan (\frac{α}{3} + 180 °) .

Überprüfe damit, ob weitere Winkel eine Lösung sein können. Es folgt daraus, dass auch

\tan (\frac{108 °}{3} + 180 °) = \tan (216 °) .

Aber $\frac{α}{3} = 216 °$ ergibt $α = 648 °$ . Der Winkel ist größer als $360 °$ und damit keine Lösung. $108 °$ ist also von diesem Teil der Gleichung die einzige Lösung.

Insgesamt wird die Gleichung von allen $α \in {37,5 °; 52,5 °; 108 °}$ gelöst.

Überarbeiten
Teilen

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0

serlo.org CC BY-SA 4.0

→ Was bedeutet das?