Volumenberechnung bei zusammengesetzten Körpern

Wenn man das Volumen eines Körpers berechnen will, kann man ihn oft in schon bekannte Körper aufteilen und damit das Volumen leichter errechnen.

Zerlegung in Quader

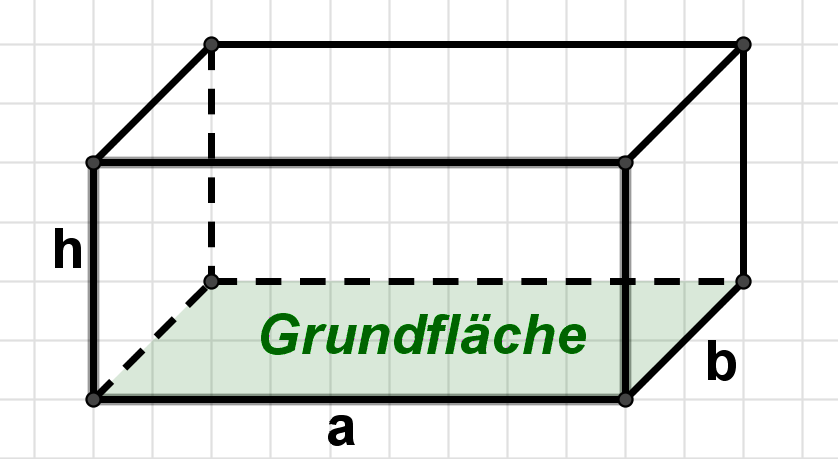
Grundwissen: Das Volumen eines Quaders

Das Volumen eines Quaders berechnet man, indem man die Grundfläche mit der Höhe multipliziert.

$V_{\text{Quader}} = G \cdot h = a\cdot b\cdot h$

Volumenberechnung durch Zerlegen in Einzelteile

Schwierigere Körper lassen sich manchmal in mehrere Quader unterteilen. Mit diesem Trick kann man dann auch ihr Volumen einfach berechnen.

Beispiel

Der Körper lässt sich zum Beispiel entlang den rot gepunkteten Linien in zwei Quader aufteilen. Du rechnest beide einzeln aus und addierst sie dann.

$V = V_{\text{Quader unten}} + V_{\text{Quader oben}} \\ \hphantom{V} = (6\ \mathrm{cm} \cdot 2\ \mathrm{cm} \cdot 1{,}5\ \mathrm{cm}) + (2\ \mathrm{cm} \cdot 2\ \mathrm{cm} \cdot 2\ \mathrm{cm}) \\\hphantom{V} = 18\ \mathrm{cm^3} + 8\ \mathrm{cm^3} = 26\ \mathrm{cm^3}$

Volumenberechnung durch Abziehen bestimmter Teile

Manchmal kann man das Volumen auch geschickter berechnen, indem man von einem größeren Körper Teile abzieht.

Beispiel

Um das Volumen dieses Körpers zu berechnen, kann man zum Beispiel zuerst den kompletten Quader mit Länge $5 \mathrm{cm}$ , Breite $2 \mathrm{cm}$ und Höhe $7 \mathrm{cm}$ berechnen. Davon zieht man dann die Lücken noch ab.

$V_\text{Quader groß} = 5\ \mathrm{cm} \cdot 2\ \mathrm{cm} \cdot 7\ \mathrm{cm} = 70\ \mathrm{cm}^3$

$V_\text{Lücke} = 3\ \mathrm{cm} \cdot 2\ \mathrm{cm} \cdot 1{,}4\ \mathrm{cm} = 8{,}4\ \mathrm{cm}^3$

$V_\text{Körper} = V_\text{Quader groß} - V_\text{Lücke} - V_\text{Lücke} = 70\ \mathrm{cm}^3 - 8{,}4\ \mathrm{cm}^3 - 8{,}4\ \mathrm{cm}^3 = 53{,}2\ \mathrm{cm}^3$

Zerlegung in Prismen und Zylinder

Grundwissen

Die Formel "Grundfläche mal Höhe" kann man nicht nur für das Volumen von Quadern verwenden, sondern bei allen Prismen und Zylindern.

$V_{\text{Prisma}}=\mathrm{G_P}\cdot\mathrm{h_p}$

$V_{\text{Zylinder}}=\mathrm{G_Z}\cdot\mathrm{h_Z}=r^2\pi\cdot\mathrm{h_Z}$

Wie man die Grundfläche berechnet, hängt von der Form der Grundfläche ab.

Für viele dieser ebenen Figuren gibt es Formeln zur Berechnung.

Volumenberechnung durch Zerlegen in Prismen und Zylinder

Mit Prismen und Zylindern kann man von vielen weiteren Körpern das Volumen berechnen.

Beispiel

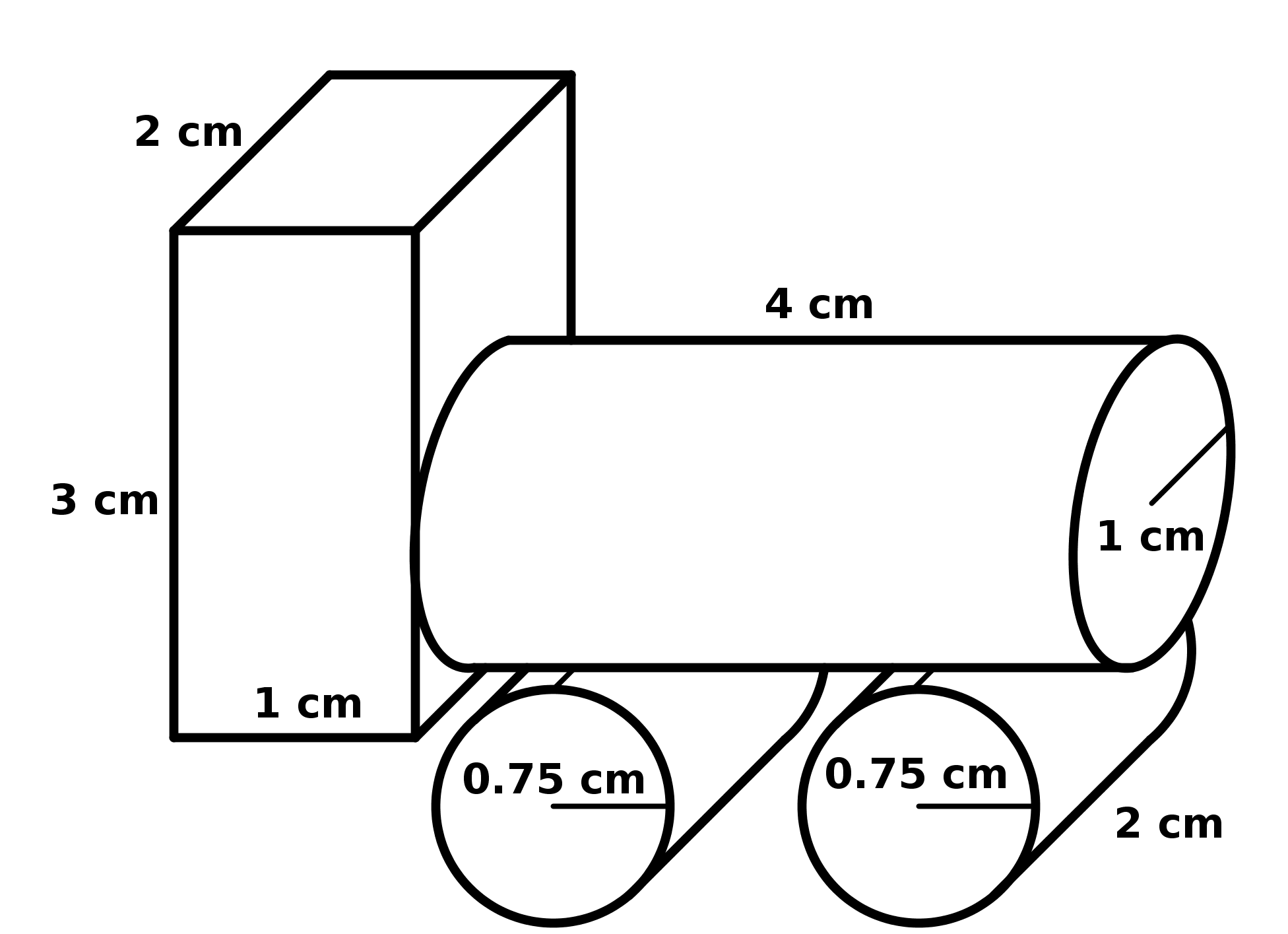
Um das Volumen dieser Spielzeuglokomotive näherungsweise auszurechnen, überlegt man sich zuerst, aus welchen Körpern sie ungefähr zusammengesetzt ist.

Ein mögliches Modell könnte so aussehen:

Man berechnet also die Volumen des Quaders, und der Zylinder

$V_{Führerstand} = 2\ \mathrm{cm}\cdot 1 \ \mathrm{cm} \cdot 3 \ \mathrm{cm} = 6 \ \mathrm{cm^3}$

$V_{Radzylinder} = (0.75\ \mathrm{cm})^2 \pi \cdot 2\ \mathrm{cm} = 1.125 \ \mathrm{cm^3} \cdot \pi \approx 3.53 \ \mathrm{cm^3}$

$V_{Rumpf} = (1\ \mathrm{cm})^2 \pi \cdot 4\ \mathrm{cm} = 4 \ \mathrm{cm^3}\cdot \pi \approx 12.57 \ \mathrm{cm^3}$

Insgesamt erhält man dann das Volumen der Lokomotive, indem man die einzelnen Teile zusammenaddiert.

$V_{Lokomotive} = V_{Führerstand} + 2 \cdot V_{Radzylinder} + V_{Rumpf} \approx 6 \ \mathrm{cm^3} + 2\cdot 3.53 \ \mathrm{cm^3} + 12.57 \ \mathrm{cm^3} = 25.63 \ \mathrm{cm^3}$

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?