Berechne möglichst geschickt die Lösungen der folgenden Gleichungen. Überprüfe deine Ergebnisse grafisch, z. B. mithilfe eines Funktionsplotters.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung
↓ Diskriminante berechnen
↓ daher 2 Lösungen
↓ In die Mitternachtsformel einsetzen dabei die berechnete Diskriminante einsetzen
↓ berechnen
Graphen zeichnen

Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung
Gleichung bestimmen
↓ Klammer mit Hilfe der 1. Binomischen Formel ausmultiplizieren.
↓ Gleiche Elemente zusammenfassen
↓ Diskriminante berechnen
↓ daher 2 Lösungen
↓ In die Mitternachtsformel einsetzten, dabei die berechnete Diskriminante einsetzen.
Graphen zeichnen

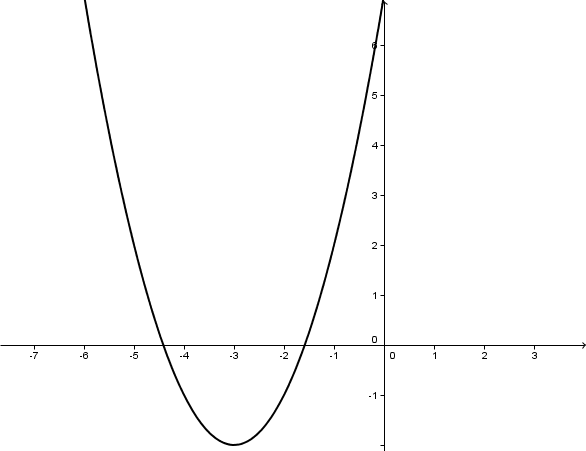
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Mitternachtsformel (Quadratische Lösungsformel)
Quadratische Gleichung lösen
↓ Stelle die Gleichung so um, dass auf einer Seite 0 ist
↓ Setze in die Mitternachtsformel ein
↓ ausrechnen
Graphische Darstellung
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Äquivalenzumformungen
Lösungen von Gleichungen
Graphen zeichen

Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Mitternachtsformel (Quadratische Lösungsformel)
Lösung mit Hilfe der pq-Formel:
↓ Die Gleichung liegt in der Normalform vor.
Nach der pq-Formel gilt:
mit und
↓ Einsetzen der Werte
↓ Vereinfachen der Wurzel
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
Quadratische Gleichung
↓ Gleiches zusammenfassen
↓ Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

