Aufgaben zum Addieren und Subtrahieren von ganzen Zahlen

Wie gut kennst du dich mit dem Addieren und Subtrahieren aus? Teste dich mit diesen gemischten Rechenaufgaben!

1
Welche Aufgabe hat das Ergebnis $- 5$ ?
$5 - 10$
$- 10 - 5$
$10 - 5$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
$10 - 5$ ist nicht richtig, weil: $10 - 5 = 5$
$- 10 - 5$ ist nicht richtig, weil: $- 10 - 5 = - 15$
$5 - 10$ ist richtig, weil: $5 - 10 = - 5$
Die richtige Aufgabe ist also: $5 - 10$ .
2
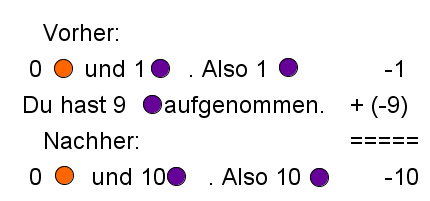
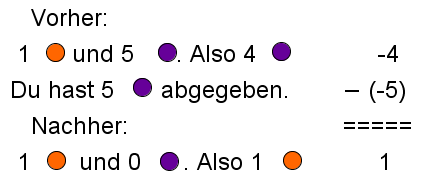
Berechne folgende Ausdrücke mit den Rechenregeln.
1. $7 - 10$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
  Lösungsweg 1
  Du ziehst von einer positiven Zahl eine größere ab. Das Ergebnis ist also negativ.
  $7 - 10 = - 3$
  Lösungsweg 2
  …mit dem Kontospiel: (Beide Möglichkeiten sind richtig.)
  Möglichkeit 1:
  Möglichkeit 2:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $1 - (- 1)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
  Lösungsweg 1
  Beachte: "Minus und Minus gibt Plus"
  $1 - (- 1) = 1 + 1 = 2$
  Lösungsweg 2
  … mit dem Kontospiel:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $- 5 + 9$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
  Lösungsweg 1
  $- 5 + 9$
  In der Rechnung steht ein Minuszeichen. Bilde also die Beträge der Zahlen.
  $| - 5 | = 5$ und $| 9 | = 9$
  Ziehe vom größeren Betrag den kleineren Betrag ab.
  $9 - 5 = 4$
  Schreibe vor die Differenz das Vorzeichen der betragsmäßig größeren Zahl. Das ist hier die $+ 9$ . Das Vorzeichen also ein Plus.
  $- 5 + 9 = 4$
  Lösungsweg 2
  … mit dem Kontospiel:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $- 1 + (- 9)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
  Lösungsweg 1
  $- 1 + (- 9)$
  Zur negativen Zahl $- 1$ kommen weitere $- 9$ hinzu.
  $- 1 + (- 9) = - 10$
  Lösungsweg 2:
  … mit dem Kontospiel:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $- 4 - (- 5)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
  Lösungsweg 1
  $- 4 - (- 5)$
  Es gilt die Regel: "Minus und Minus ergibt Plus"
  $- 4 + 5$
  Zur negativen Zahl $- 4$ wird eine positive Zahl mit größerem Betrag addiert. Das Ergebnis ist also positiv.
  $- 4 + 5 = 1$
  Lösungsweg 2
  …mit dem Kontospiel:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. $- 5 - 9$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtrakiton ganzer Zahlen
  $- 5 - 9$
  Von der negativen Zahl $- 5$ werden weitere $9$ abgezogen.
  $- 5 - 9 = - 14$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. $4 - (- 8)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
  $4 - (- 8)$
  Aus Minus und Minus wird Plus.
  $4 - (- 8) = 4 + 8 = 12$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8. $- 17 + 10$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
  $- 17 + 10 = - 7$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
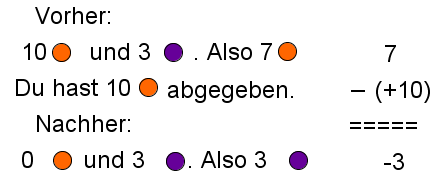
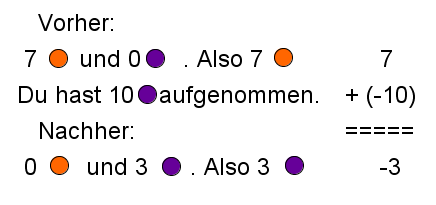
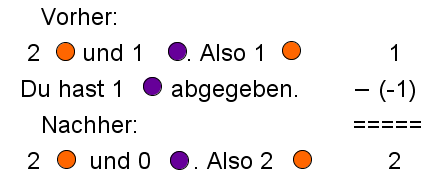
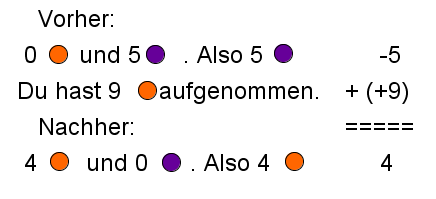
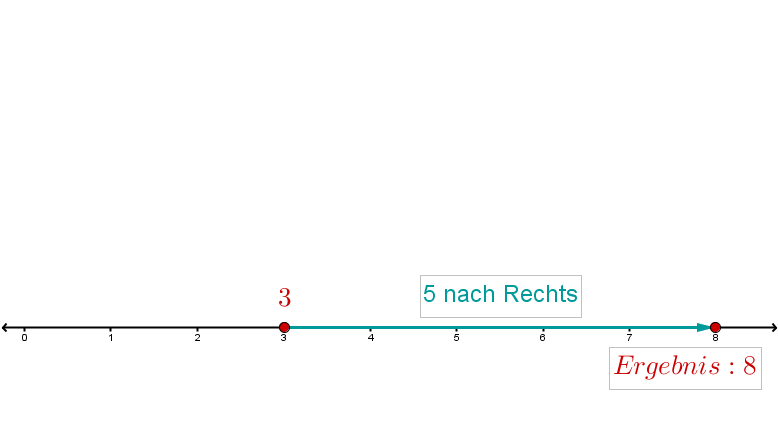
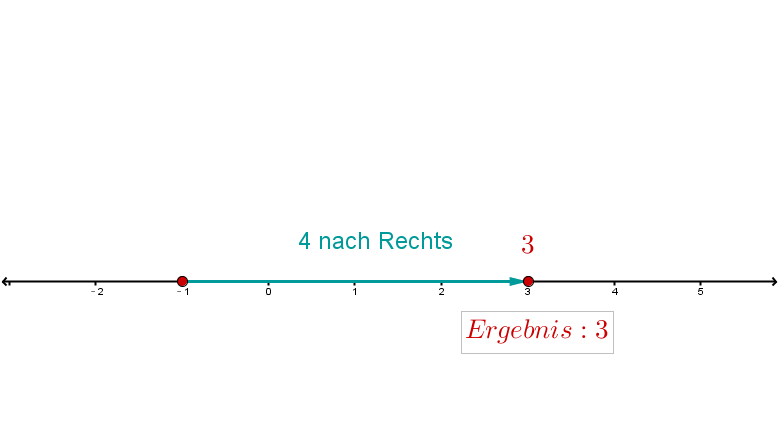
Führe folgende Additionen/Subtraktionen mit Hilfe einer Zahlengeraden durch:
1. $3 + 5$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition auf der Zahlengerade
  Gehe vom Nullpunkt aus $3$ Schritte nach rechts, um $3$ zu finden.
  Da es sich um eine Addition handelt, gehe $5$ Schritte nach rechts.
  Das Ergebnis ist $3 + 5 = 8$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $- 1 + 4$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition auf der Zahlengerade
  Da $- 1$ eine negative Zahl ist, muss man vom Nullpunkt aus einen Schritt nach links gehen, um $- 1$ zu finden.
  Gehe $4$ Schritte nach rechts, da es sich um eine Addition handelt.
  Das Ergebnis ist $- 1 + 4 = 3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $- 2 - 1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition auf der Zahlengerade
  Da $- 2$ eine negative Zahl ist, muss man vom Nullpunkt aus $2$ Schritte nach links gehen, um $- 2$ zu finden.
  Gehe einen Schritt nach links, da es sich um eine Subtraktion handelt.
  Das Ergebnis ist $- 2 - 1 = - 3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Was ist die Lösung der Differenz $8765 - 43210$ ?
Begründe ohne Rechnung.
$- 34445$
$- 3445$
$- 35554$
$3445$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
Eine Überschlagsrechnung ergibt:
$8765 - 43210 \approx 9000 - 43000 = - 34000$
Damit kommen nur noch $- 35554$ oder $- 34445$ als mögliche Lösungen in Frage.
Die Betrachtung der letzten Ziffern ergibt: $5 - 0 = 5$ . Damit muss auch die letzte Ziffer der Lösung eine $5$ sein.
Also ist $- 34445$ das korrekte Ergebnis.

Berechne:

\begin{array}{l} 12 + 722 + [(22 \cdot 84 + 11 - 22) + 15 - 22 + (- 12 + 25)] \end{array}

6
Subtrahiere von der kleinsten ungeraden dreistelligen Zahl die Summe der vier größten zweistelligen Zahlen.
Du kannst dein Ergebnis im Eingabefeld überprüfen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Grundrechenarten
Zahlen bestimmen
Kleinste ungerade dreistellige Zahl: $101$
Vier größten zweistelligen Zahlen: $99, 98, 97, 96$
Wert des Terms berechnen
$101 - (99 + 98 + 97 + 96)$
↓
In der Klammer addieren .
$=$ $101 - 390$
↓
Subtrahiere.
$=$ $- 289$
7
Zähle die Rechenzeichen auf und begründe, welches Zeichen in der angegebenen Term ein Rechenzeichen ist.
$- 5 + (- 1) + 4 + (- 1)$

Lösung:
$- 5 + (- 1) + 4 + (- 1)$
Die orange markierten Zeichen sind Rechenzeichen. Das Minus vor der $5$ am Anfang und den beiden $1$ en sind Vorzeichen der Zahl und somit kein Rechenzeichen.
Hierbei schauen wir uns die Vorzeichen der Zahlen von links nach rechts an und kontrollieren ob es ein Vorzeichen der Zahl ist, oder ein Rechenzeichen ist.
8
Fülle die Lücken.
1. $- 148 -__= 256$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Subtraktion
  Überlegung: Welche Zahl muss von $- 148$ subtrahiert werden, um $256$ zu erhalten?
  Stelle nach der unbekannten Zahl um.
  $- 148 -__$ $=$ $256$
  $- 148$ $=$ $256 +__$
  $- 148 - 256$ $=$ $__$
  $- 404$ $=$ $__$
  Setze $- 404$ in die Anfangsgleichung ein:
  $- 148 - (- 404) = - 148 + 404 = 256$
  Das Ergebnis ist richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $287 +__= - 211$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition
  Überlegung: Welche Zahl muss man zu $287$ addieren, um $- 211$ zu erhalten?
  Stelle nach der unbekannten Zahl um.
  $287 +__$ $=$ $- 211$
  $__$ $=$ $- 211 - 287$
  $__$ $=$ $- 498$
  Setze $- 498$ in die Anfangsgleichung ein:
  $287 + (- 498) = 287 - 498 = - 211$
  Das Ergebnis ist richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $389 -__= 523$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Subtraktion
  Überlegung: Welche Zahl muss von $389$ subtrahiert werden, um $523$ zu erhalten?
  Stelle nach der unbekannten Zahl um.
  $389 -__$ $=$ $523$
  $389$ $=$ $523 +__$
  $389 - 523$ $=$ $__$
  $- 134$ $=$ $__$
  Setze $- 134$ in die Anfangsgleichung ein:
  $389 - (- 134) = 389 + 134 = 523$
  Das Ergebnis ist richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $- 148 +__= 1347$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition
  Überlegung: Welche Zahl muss man zu $287$ addieren, um $- 211$ zu erhalten?
  Stelle nach der unbekannten Zahl um.
  $- 148 +__$ $=$ $1347$
  $__$ $=$ $1347 + 148$
  $__$ $=$ $1495$
  Setze $1495$ in die Anfangsgleichung ein:
  $- 148 + 1495 = 1495 - 148 = 1347$
  Das Ergebnis ist richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $14 - [__] = - 70$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Subtraktion
  $14 - [__] = - 70$
  Überlegung: Welche Zahl muss man von 14 subtrahieren, um $- 70$ zu erhalten?
  $\Rightarrow$ Um von $14$ auf $0$ zu kommen, muss man $14$ abziehen. Um von $0$ auf $- 70$ zu kommen, weitere $70$ .
  $14 + 70 = 84$
  $\Rightarrow 14 - 84 = - 70$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
  $- 2005 -__= 2006$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Subtraktion
  $- 2005 -__= 2006$
  Überlegung: Welche Zahl muss von $- 2005$ subtrahiert werden, um $2006$ zu erhalten?
  Stelle nach der unbekannten Zahl um.
  $- 2005 -__$ $=$ $2006$
  ↓
  addiere auf beiden Seiten 2005 und multipliziere anschließend beide Seiten mit (-1)
  $__$ $=$ $- 2006 - 2005$
  $__$ $=$ $- 4011$
  Setze $- 4011$ in die Anfangsgleichung ein.
  $- 2005 - (- 4011) = 2006$
  Das Ergebnis ist richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9
Welche Aufgaben ergeben das Ergebnis $10$ ?
$- 5 - (- 15)$
$- 5 + 15$
$- 8 + (- 2)$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition von ganzen Zahlen
Lösung für:
$- 5 - (- 15)$
Löse die Klammer auf.
$= - 5 + 15 = 10$
Lösung für:
$- 5 - (- 15)$
Löse die Klammer auf.
$= - 5 + 15 = 10$
Lösung für:
$- 8 + (- 2)$
Löse die Klammer auf
$- 8 - 2 = - 10$
Zwei Aufgaben haben das Ergebnis $10$ . Richtig sind somit:
$- 5 + 15$ und $- 5 - (- 15)$
10
Schreibe das richtige Vorzeichen („+“ oder „-“) in die Lücke.
1. $□ 34 - 20 = - 54$
  $+$
  $-$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion von ganzen Zahlen
  $- 25 - 10 = - 35$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $- 76 + 82 = □ 6$
  $+$
  $-$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion von ganzen Zahlen
  $- 76 + 82 = + 6$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $+ 36 - 79 = □ 43$
  +
  $-$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion von ganzen Zahlen
  $+ 36 - 79 = - 43$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $- 86 + 38 = □ 48$
  $+$
  $-$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion von ganzen Zahlen
  $- 86 + 38 = - 48$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $□ 56 + 75 = 131$
  $+$
  $-$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion von ganzen Zahlen
  $+ 56 + 75 = 131$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. $- 91 + 36 = □ 55$
  $+$
  $-$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion von ganzen Zahlen
  $- 91 + 36 = - 55$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. $□ 23 - 76 = - 53$
  $+$
  $-$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion von ganzen Zahlen
  $+ 23 - 76 = - 53$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8. $□ 176 - 298 = - 474$
  $+$
  $-$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion von ganzen Zahlen
  $- 176 - 298 = - 474$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9. $- 576 + 297 = □ 279$
  $+$
  $-$
  
  $- 576 + 297 = - 279$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
10. $□ 349 + 394 = 45$
  $+$
  $-$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion von ganzen Zahlen
  $- 349 + 394 = 45$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
11. $- 834 + 849 = □ 15$
  $+$
  $-$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion von ganzen Zahlen
  $- 834 + 849 = 15$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
12. $763 - 761 = □ 2$
  $+$
  $-$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion von ganzen Zahlen
  $763 - 761 = + 2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
13. $763 - 765 = □ 2$
  $+$
  $-$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion von ganzen Zahlen
  $763 - 765 = - 2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
11
Gegeben ist der Term $13 - (12 - 21) - (- 14 + 41)$ .
1. Berechne den Termwert.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion
  $13 - (12 - 21) - (- 14 + 41)$
  ↓
  In den Klammern subtrahieren bzw. addieren .
  $=$ $13 - (- 9) - 27$
  ↓
  Addieren, denn: "Minus und Minus gibt Plus".
  $=$ $22 - 27$
  ↓
  Subtrahieren
  $=$ $- 5$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Ändere eine Zahl des Terms so ab, dass der neue Term den Wert Null annimmt.
  
  Der Wert des Termes beträgt $- 5$ .
  Damit der Term $0$ ergibt, muss eine der Zahlen, die nicht subtrahiert werden, um $5$ erhöht werden.
  Das einfachste ist, die $13$ zu $18$ zu ändern
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
12
Nachdem 100€ auf das Konto eingezahlt worden sind, beträgt der Kontostand 20€.
1. Wie hoch war der Kontostand vor der Einzahlung? (in €)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
  Nachdem zum alten Kontostand 100€ hinzugekommen sind, beträgt der neue Kontostand 20€.
  Mache einen Ansatz mit einer unbestimmten Größe, dem alten Kontostand.
  Rechne zunächst ohne Einheiten.
  $x + 100$ $=$ $20$ $- 100$
  $x$ $=$ $20 - 100 = - 80$
  Der alte Kontostand betrug also -80€, d.h. das Konto war mit 80€ überzogen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Wie viel muss nun abgehoben werden, um einen Kontostand von -50€ zu erreichen?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition und Subtraktion ganzer Zahlen
  Mache nun einen Ansatz mit der Abhebung als unbekannte Größe.
  Rechne zunächst ohne Einheiten.
  $20 - x$ $=$ $- 50$
  $x$ $=$ $20 + 50 = 70$
  Nach einer Abhebung von 70€ beträgt der Kontostand also -50€.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Gegeben ist der Term $4 - (89 + 18) - (25 - 73)$ .

Mache zuerst eine Überschlagsrechnung.

Berechne anschließend den genauen Termwert und überprüfe diesen mithilfe des Eingabefelds.

Wie ändert sich der Wert des Terms, wenn leichtsinnigerweise statt 89 die Zahl 98 abgeschrieben wurde? Begründe deine Antwort ohne neue Rechnung.

Überlegung:
$98$ ist um $9$ größer als $89$ . Im Term wird $89$ subtrahiert.
Also wird der Gesamtwert des Termes kleiner, wenn $89$ durch $98$ ersetzt wird.
Der Wert des neuen Terms wäre dann genau um 9 kleiner als der Wert des Ursprungsterms.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

	$4 - (89 + 18) - (25 - 73)$
	↓ Um das Ergebnis zu überschlagen, werden die Werte auf Zehner gerundet.
$=$	$0 - (90 + 20) - (30 - 70)$
	↓ Addiere und subtrahiere in den beiden inneren Klammern.
$=$	$- 110 - (- 40)$
	↓ "Minus und Minus gibt Plus".
$=$	$- 110 + 40$
	↓ Addiere.
$=$	$- 70$

	$4 - (89 + 18) - (25 - 73)$
	↓ Addiere und subtrahiere in den beiden inneren Klammern.
$=$	$4 - 107 - (- 48)$
	↓ Subtrahiere.
$=$	$- 103 - (- 48)$
	↓ "Minus und Minus gibt Plus".
$=$	$- 103 + 48$
	↓ Addiere.
$=$	$- 55$

	$=$	$12 + 722 + [(1848 + 11 - 22) + 15 - 22 + (- 12 + 25)]$
	↓	Berechne $12 + 722$ und $15 - 22$ (mitten in der eckigen Klammer) und die hintere runde Klammer.
	$=$	$734 + [(1848 + 11 - 22) - 7 + (+ 13)]$
	↓	Berechne den Term in der runden Klammer und $- 7 + (+ 13)$ .
	$=$	$734 + [(+ 1837) + 6]$
	↓	Berechne die eckige Klammer.
	$=$	$2571 + 6$
	$=$	$2577$

	$101 - (99 + 98 + 97 + 96)$
	↓ In der Klammer addieren .
$=$	$101 - 390$
	↓ Subtrahiere.
$=$	$- 289$

$- 148 -__$	$=$	$256$
$- 148$	$=$	$256 +__$
$- 148 - 256$	$=$	$__$
$- 404$	$=$	$__$

$389 -__$	$=$	$523$
$389$	$=$	$523 +__$
$389 - 523$	$=$	$__$
$- 134$	$=$	$__$

$- 2005 -__$	$=$	$2006$
	↓	addiere auf beiden Seiten 2005 und multipliziere anschließend beide Seiten mit (-1)
$__$	$=$	$- 2006 - 2005$
$__$	$=$	$- 4011$

	$13 - (12 - 21) - (- 14 + 41)$
	↓ In den Klammern subtrahieren bzw. addieren .
$=$	$13 - (- 9) - 27$
	↓ Addieren, denn: "Minus und Minus gibt Plus".
$=$	$22 - 27$
	↓ Subtrahieren
$=$	$- 5$

$x + 100$	$=$	$20$	$- 100$
$x$	$=$	$20 - 100 = - 80$

$20 - x$	$=$	$- 50$
$x$	$=$	$20 + 50 = 70$

Aufgaben zum Addieren und Subtrahieren von ganzen Zahlen

Lösungsweg 1

Lösungsweg 2

Hast du eine Frage oder Feedback?

Lösungsweg 1

Lösungsweg 2

Hast du eine Frage oder Feedback?

Lösungsweg 1

Lösungsweg 2

Hast du eine Frage oder Feedback?

Lösungsweg 1

Lösungsweg 2:

Hast du eine Frage oder Feedback?

Lösungsweg 1

Lösungsweg 2

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Zahlen bestimmen

Wert des Terms berechnen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?