Aufgaben zum Zylinder

Hier findest du verschiedene Aufgaben rund um den Zylinder. Teste dein Wissen, berechne Oberflächen und Volumen oder finde Zylindernetze.

1
Finde Beispiele für Objekte, die ungefähr zylinderförmig sind, zum Beispiel Gegenstände aus dem Alltag, der Technik, der Natur oder der Architektur.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
Beispiele für Gegenstände, die ungefähr die Form eines Zylinders haben:
Mülleimer
Benzinfass
Plakatsäule
2
Der Durchmesser des Mülleimers ist 30 cm und die Höhe ist 60 cm (ohne den Deckel). Wie groß ist das Volumen?
Runde auf ganze $c m^{3} cm³$ .
cm³

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
$V=r^2 \cdot \pi \cdot h$
Das ist die Formel für das Volumen eines Zylinders.
Die Höhe 60 cm ist in der Aufgabe angegeben, den Radius berechnest du aus dem Durchmesser.
$r= d:2= 30\, \text{cm} :2 = 15\, \text{cm}$
Nun kannst du in die Volumenformel einsetzen.
$V=(15\, \text{cm})^2 \cdot \pi \cdot 60\,\text{cm}$
Das rechnest du aus,
$=13\, 500 \cdot \pi\ \text{cm}^3$
$= 42\,411{,}5008….\, \text{cm}^3$
und rundest das Ergebnis.
$\approx 42\,412\, \text{cm}^3$
3
Dieses Glas hat einen Durchmesser von 7 cm und seine Höhe ist 8 cm.
Berechne das Volumen des Glases. Runde dein Ergebnis auf Einer.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
$V=r^2\cdot\mathrm{\pi}\cdot\mathrm{h}$
Das ist die Formel für das Volumen eines Zylinder. Die Höhe 8 cm ist in der Aufgabe angegeben, den Radius berechnest du aus dem Durchmesser. Nun kannst du in die Volumenformel einsetzen.
$V=(3{,}5\;\mathrm{cm})^2\cdot\;\mathrm\pi\;\cdot\;8\;\mathrm{cm}$
$\;\;\;=\;98\cdot\mathrm\pi\;\mathrm{cm}^3$
$\;\;\;=\;307{,}876…\;\mathrm{cm}^3$
$\;\;\;\;\;\approx\;308\;\mathrm{cm}^3$
4
Gegeben ist ein Zylinder mit einem Durchmesser von $8 m$ und einer Höhe von $5 m$ .
Berechne das Volumen, die Mantelfläche und die Oberfläche des Zylinders.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen, Mantelfläche und Oberfläche eines Zylinders
Der Radius $r$ ist halb so lang wie der Durchmesser, also gilt $r=4\ \text{m}$ .
$\def\arraystretch{1.25} \begin{array}{l}V=r^2\mathrm{πh}\\\mathrm M=2\mathrm{rπh}\\\mathrm O=2\mathrm r^2\mathrm\pi+2\mathrm{rπh}\end{array}$
$V=r^2\mathrm{πh}=(4\mathrm m)^2\cdot3{,}14\cdot5\mathrm m=16\mathrm m^2\cdot3{,}14\cdot5\mathrm m=251{,}2\mathrm m^3$
$M=2r\mathrm{πh}=2(4\mathrm m)\cdot3{,}14\cdot5\mathrm m=8\mathrm m\cdot3{,}14\cdot5\mathrm m=125{,}6\mathrm m^2$
$O=2r^2\mathrm\pi+2\mathrm{rπh}=2(4\mathrm m)^2\cdot3{,}14+2\cdot4\mathrm m\cdot3{,}14\cdot5\mathrm m$
$\;\;\;\;=100{,}48\mathrm m^2+125{,}60\mathrm m^2=226{,}08\mathrm m^2$
Das Volumen des Zylinders beträgt $251{,}2m^3$ , die Mantelfläche $125{,}6m^2$ und die Oberfläche $226{,}08m^2$ .
5
Gegeben ist ein Zylinder mit einer Oberfläche von $150{,}72cm^2$ und einem Durchmesser von $6 c m$ .
Berechne die Höhe des Zylinders.
cm

Für diese Aufgabe benötigst Du folgendes Grundwissen: Oberfläche eines Zylinders
$O=2r^2\mathrm\pi+2\mathrm{rπh} \quad | -2r^2\mathrm\pi$
$O-2r^2\mathrm\pi=2\mathrm r\mathrm\pi\mathrm h \quad | :2r\mathrm\pi$
$h=\cfrac{O-2r^2\mathrm\pi}{2r\mathrm\pi}$
$h=\dfrac{150{,}72-2\cdot9\cdot3{,}14}{2\cdot3\cdot3{,}14}=\dfrac{150{,}72-56{,}52}{18{,}84}=\dfrac{94{,}2}{18{,}84}=5$
Die Höhe des Zylinders beträgt $5 c m$ .
6
Herr Müller möchte ein Kabel mit einem Volumen von $0{,}63 \,\mathrm{m^3}$ verlegen. Der Radius beträgt $10 \,\mathrm{cm}$ . Berechne die Länge des Kabels. Runde beim Ergebnis auf ganze Zahlen.
m

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
Die allgemeine Formel für das Volumen eines Zylinders ist:
$\displaystyle V = \pi r^2 \cdot l$
Da die Länge $l$ gesucht ist, musst du die Formel danach auflösen, wie folgt:
$\displaystyle V = \pi r^2 \cdot l \Rightarrow l = \dfrac{V}{\pi r^2}$
Nun brauchst du nur noch die Werte einzusetzen. Hierbei musst du beachten, dass der Radius in $\mathrm{cm}$ angegeben ist und in $\mathrm{m}$ umgerechnet werden muss:
$\displaystyle \def\arraystretch{2} \begin{array}{rcl} l &=& \dfrac{V}{\pi r^2} \\\\ l &=& \dfrac{0{,}63 \,\mathrm{m^3}}{\pi \cdot (10 \,\mathrm{cm})^2} \\\\ l &=& \dfrac{0{,}63 \,\mathrm{m^3}}{\pi \cdot (0{,}1 \,\mathrm{m})^2} \\\\ l &=& 20 \,\mathrm{m} \end{array}$
Das heißt, dass die Länge des Kabels $20 \,\mathrm{m}$ beträgt.
7
Eine Getränkedose hat eine Höhe $h$ von $16{,}8 \text{cm}$ . Der Durchmesser $d$ beträgt $6{,}7 \text{cm}$ . Berechne das Volumen der Dose.
Runde dein Ergebnis auf ganze Zahlen.
cm³

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
Die allgemeine Formel zur Berechnung des Volumens eines Zylinders ist:
$\displaystyle V_{\mathrm{Zyl}} = \pi r^2 \cdot h$
Da der Durchmesser gegeben ist, musst du den Radius daraus erechnen, wie folgt:
$\displaystyle \def\arraystretch{2} \begin{array}{rcl} d = 2r \Rightarrow r &=& \dfrac{1}{2}d \\\\ r &=& \dfrac{1}{2} \cdot 6{,}7 \mathrm{cm} = 3{,}35 \mathrm{cm} \end{array}$
Nun kannst du die Werte in die Formel einsetzen, um das Volumen zu berechnen.
$\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} V_{\mathrm{Zyl}} &=& \pi r^2 \cdot h \\ V_{\mathrm{Zyl}} &=& \pi \cdot (3{,}35 \,\mathrm{cm})^2 \cdot 16{,}8 \,\mathrm{cm} \\ V_{\mathrm{Zyl}} &=& 592 \,\mathrm{cm}^3 \end{array}$
Daraus folgt, dass das Volumen des Zylinders $592 \,\mathrm{cm}^3$ beträgt.
8
Ein zylinderförmiger Lautsprecher hat eine Höhe von $h = 18 \,\mathrm{cm}$ . Der Radius beträgt $r = 3{,}75 \,\mathrm{cm}$ . Berechne das Volumen.
Runde dein Ergebnis auf ganze Zahlen.
cm³

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
Die allgemeine Formel zur Berechnung des Volumens eines Zylinders ist:
$\displaystyle V_{\mathrm{Zyl}} = \pi r^2 \cdot h$
In diese Formel setzt du nun die gegebnen Werte ein.
$\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} V_{\mathrm{Zyl}} &=& \pi r^2 \cdot h \\ V_{\mathrm{Zyl}} &=& \pi \cdot (3{,}75 \,\mathrm{cm})^2 \cdot 18 \,\mathrm{cm} \\ V_{\mathrm{Zyl}} &\approx& 795 \,\mathrm{cm^3} \end{array}$
Daraus folgt, dass das Volumen des Zylinders ca. $795 \,\mathrm{cm^3}$ beträgt.
9
Welche Aussagen zu Zylindern sind richtig?
Ein Zylinder kann als Grundfläche jede beliebige Fläche haben.
Wenn man die Mantelfläche eines Zylinders ausbreitet, entsteht ein Rechteck.
Wenn ich die Höhe des Zylinders verdopple, erhalte ich den doppelten Flächeninhalt der Mantelfläche.
Die Mantelfläche ist ein Quadrat, wenn Höhe und Umfang der Grundfläche gleich lang sind.
Ein Zylinder hat keine Ecken, aber 2 Kanten und 3 Flächen.
Die Deck- und Grundfläche liegen parallel übereinander.
10
Ein Zylinder hat eine Höhe von $5\textsf{ cm}$ . Die Grundfläche (also der Kreis) hat einen Durchmesser von $4\textsf{ cm}$ und einen Umfang von $12{,}5\textsf{ cm}$ .
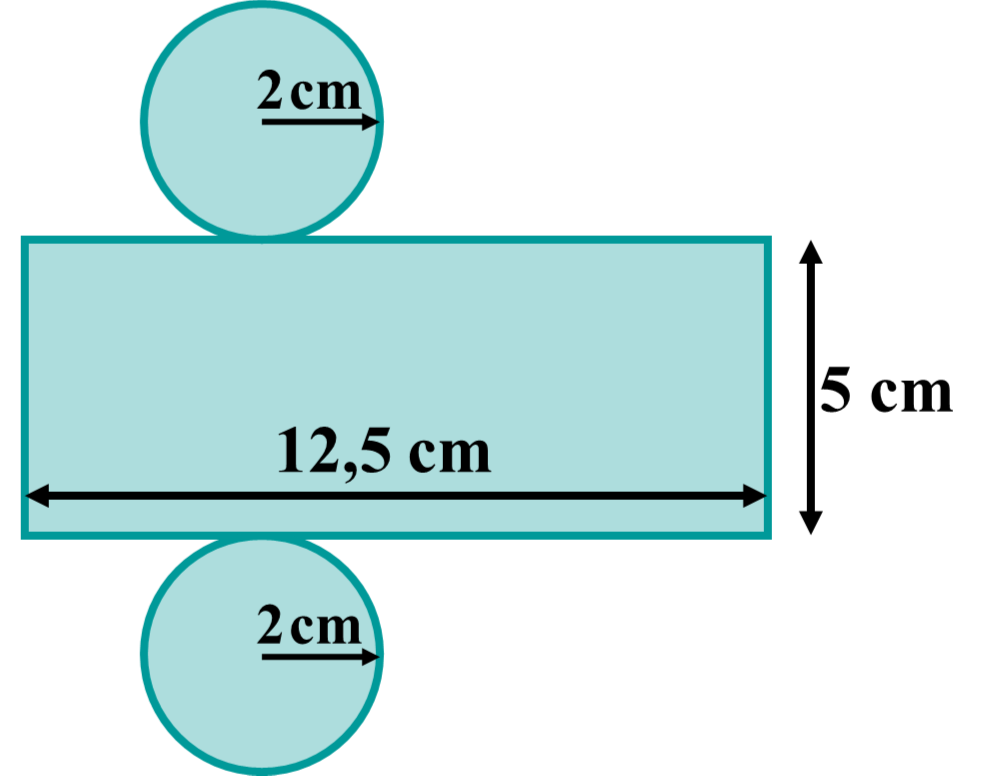
Zeichne das Körpernetz des Zylinders.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Körpernetze
Das Körpernetz des Zylinders besteht aus 3 Geometrischen Figuren. Darunter sind zwei gleich große Kreise und ein Rechteck.
Die Kreise bilden den Deckel und den Boden, das Rechteck den Mantel.
Der Radius der Kreise ergibt sich indem man den Durchmesser halbiert:
$r=\dfrac{4\textsf{ cm}}{2}=2\textsf{ cm}$
Die Mittelpunkte der Kreise haben also einen Abstand von $2\textsf{ cm}$ zum Rechteck.
Das Rechteck hat eine Breite von $5\textsf{ cm}$ . Das entspricht dem Abstand zwischen den Kreisen, also der Höhe des Zylinders.
Die Länge von $12{,}5\textsf{ cm}$ von dem Rechteck ergibt sich aus dem Umfang eines Kreises.
11
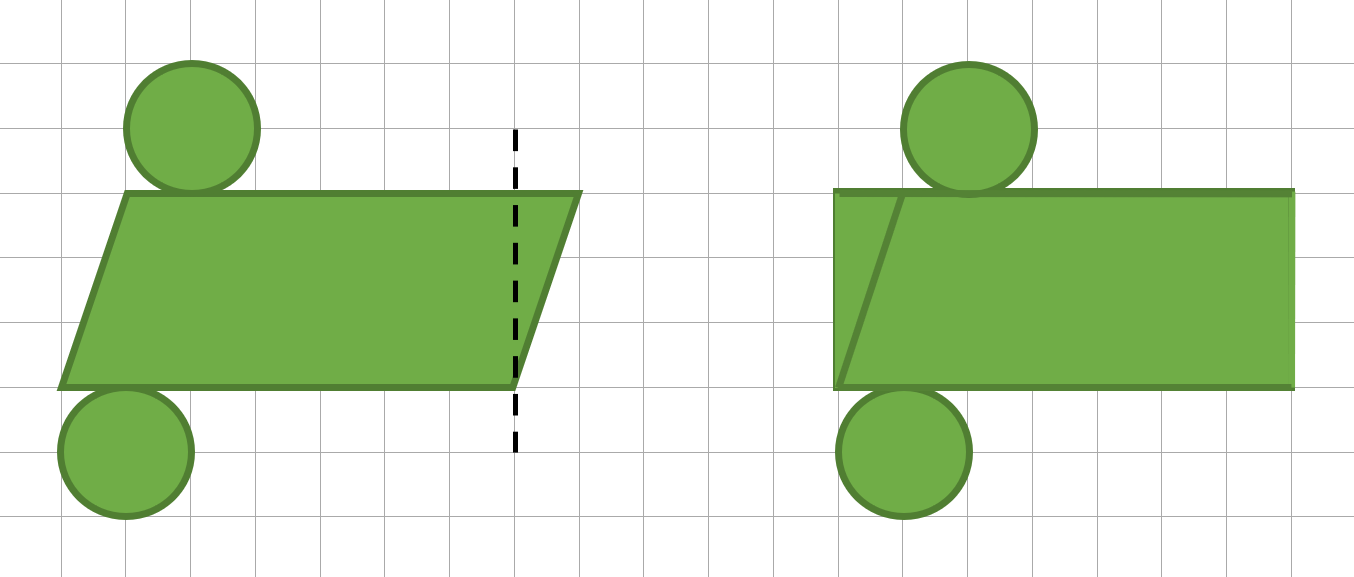
Entscheide und begründe, welche Netze einen Zylinder darstellen könnten:
Netz blau
Netz grün
Netz orange
Netz gelb
Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
Netz blau
Dies könnte ein Netz eines Zylinders sein. Man hat 2 deckungsgleiche Kreise als Deck- und Grundfläche. Außerdem scheint auf den ersten Blick, dass die Breite der Mantelfläche ungefähr der Länge des Umfangs entspricht.
Netz grün
Du hast gelernt, dass die ausgerollte Mantelfläche eines Zylinders ein Rechteck darstellt. Deswegen ist dies kein klassisches Netz eines Zylinders. Wenn du jetzt aber von rechts ein rechtwinkliges Dreieck "abschneidest" und links wieder dransetzt, dann erkennst du dass ein Rechteck entsteht.
Zusätzlich zu dem entstandenen Rechteck hast du 2 deckungsgleiche Kreise als Deck- und Grundfläche. Du kannst also davon ausgehen, dass wenn man das Netz zusammenbaut, ein Zylinder entsteht.
Netz orange
Dies könnte ein Netz eines Zylinders sein. Man hat 2 deckungsgleiche Kreise als Deck- und Grundfläche. Außerdem scheint auf den ersten Blick, dass die Breite der Mantelfläche ungefähr der Länge des Umfangs entspricht.
Netz gelb
Dies ist kein Netz von einem Zylinder, da die Deck- und die Grundfläche nicht deckungsgleich sind.
12
Ein Zylinder besitzt die folgende Maße: Radius $r = 10 \,\mathrm{cm}$ und Höhe $h = 30 \,\mathrm{cm}$ . Berechne die Oberfläche. Runde das Ergebnis auf ganze Zahlen.
cm²

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
Die Formel für die Oberfläche setzt sich zusammen aus dem Flächeninhalt zweier Kreise und des Mantels. Das heißt, dass du die Oberfläche mit folgender Formel berechnen kannst:
$\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} O_{\mathrm{Zylinder}} &=& 2 \cdot A_{\mathrm{Kreis}} &+& A_{\mathrm{Zylindermantel}} \\ O_{\mathrm{Zylinder}} &=& 2\pi r^2 &+& 2\pi rh \\ O_{\mathrm{Zylinder}} &=& 2\pi \cdot (10 \,\mathrm{cm})^2 &+& 2\pi \cdot 10 \,\mathrm{cm} \cdot 30 \,\mathrm{cm} \\ O_{\mathrm{Zylinder}} &=& \pi \cdot 200 \,\mathrm{cm^2} &+& \pi \cdot 600 \,\mathrm{cm^2} \\ O_{\mathrm{Zylinder}} &=& \pi \cdot 800 \,\mathrm{cm^2} \approx 2513 \,\mathrm{cm^2} \end{array}$
Der Zylinder besitzt eine Oberfläche von ca. $2513 \,\mathrm{cm^2}$ .
13
Ein Zylinder hat eine Oberfläche von $O_{\mathrm{Zylinder}} = 50 \,\mathrm{cm^2}$ . Der Radius beträgt $r = 2 \,\mathrm{cm}$ . Berechne die Höhe $h$ des Zylinders. Runde das Ergebnis auf ganze Zahlen.
cm

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
Die allgemeine Formel zur Berechnung der Oberfläche des Zylinders ist:
$\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} O_{\mathrm{Zylinder}} &=& 2 \cdot A_{\mathrm{Kreis}} &+& A_{\mathrm{Mantel}} \\ O_{\mathrm{Zylinder}} &=& 2\pi r^2 &+& 2\pi rh \end{array}$
Diese Formel musst du nach $h$ umstellen.
$\displaystyle \def\arraystretch{2} \begin{array}{rcl} O_{\mathrm{Zylinder}} &=& 2\pi r^2 &+& 2\pi rh \\\\ O_{\mathrm{Zylinder}} - 2 \pi r^2 &=& 2 \pi rh \\\\ \dfrac{O_{\mathrm{Zylinder}} - 2\pi r^2}{2\pi r} &=& h \\\\ \dfrac{50 \,\mathrm{cm^2} - 2\pi (2 \,\mathrm{cm})^2}{2\pi \cdot 2\,\mathrm{cm}} &=& h \\\\ \dfrac{50 \,\mathrm{cm^2} - \pi \cdot 8 \,\mathrm{cm}^2}{\pi \cdot 4\,\mathrm{cm}} &=& h \\\\ h &\approx& 2 \,\mathrm{cm} \end{array}$
Daraus folgt, dass der Zylinder eine Höhe von ca. 2 cm hat.

Berechne jeweils die gesuchten Größen für einen geraden Zylinder.

Berechne außerdem jeweils das Volumen des Zylinders.

Rechne immer mit $\pi\approx 3{,}14$ .

Gegeben sind der Oberflächeninhalt $O_{Zyl} = 351{,}68\;\text{cm}^2$ und die Mantelfläche $A_M = 251{,}2 \;\text{cm}^2$ .

Berechne die Fläche des Grundkreises $A_{K}$ , den Radius $r$ des Grundkreises und die Höhe $h$ des Zylinders.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder

Gegeben: Oberflächeninhalt $O_{Zyl}$ und Mantelfläche $A_{M}$

Gesucht: Fläche des Grundkreises $A_{K}$ , Radius $r$ des Grundkreises, Höhe $h$ des Zylinders und das Volumen $V_{Zyl}$

Benötigte Formeln:

Oberfläche des Zylinders : $O_{Zyl}=2\cdot A_K+A_M$
Mantelfläche des Zylinders: $A_M=2\cdot r \cdot \pi \cdot h $
Fläche des Grundkreises: $A_K=r^2\cdot\pi$
Volumen des Zylinders: $V_{Zyl}=A_K \cdot h$ oder $V_{Zyl}=r^2 \cdot \pi \cdot h$

Berechnung der Grundkreisfläche

Du kennst den Wert des Oberflächeninhalts $O_{Zyl}$ und den Wert der Mantelfläche $A_{M}$ des Zylinders. Somit kannst du die Formel für den Oberflächeninhalt (Nr. 1) nach $A_{K}$ auflösen.

$\displaystyle O_{Zyl}$	$=$	$\displaystyle 2\cdot A_K+A_M$	$\displaystyle -A_M$
	↓	Löse nach $A_{K}$ auf.
$\displaystyle O_{Zyl}-A_M$	$=$	$\displaystyle 2\cdot A_K$	$\displaystyle :2$
$\displaystyle \frac{O_{Zyl}-A_M}{2}$	$=$	$\displaystyle A_K$
	↓	Setze $O_{Zyl}=351{,}68\text{cm}^2$ und $A_M=251{,}2\text{cm}^2$ ein.
$\displaystyle A_K$	$=$	$\displaystyle \frac{351{,}68\text{cm}^2-251{,}2\text{cm}^2}{2}$
$\displaystyle A_K$	$=$	$\displaystyle \frac{100{,}48\ \text{cm}^2}{2}$
$\displaystyle A_K$	$=$	$\displaystyle 50{,}24\ \text{cm}^2$

Antwort: Der Grundkreis des Zylinders hat eine Fläche von etwa $50{,}24\;\text{cm}^2$ .

Berechnung des Radius der Grundkreisfläche

Du kennst die Formel für die Grundkreisfläche $A_{K}$ des Zylinders (Nr. 3).

Benutze den gerade berechneten Wert der Grundkreisfläche um den Radius $r$ zu berechnen.

$\displaystyle A_K$	$=$	$\displaystyle r^2\cdot \pi$	$\displaystyle :\pi$
	↓	Löse nach $r$ auf.
$\displaystyle \dfrac{A_K}{\pi}$	$=$	$\displaystyle r^2$	$\displaystyle \sqrt{}$
$\displaystyle r$	$=$	$\displaystyle \sqrt{\dfrac{A_K}{\pi}}$
	↓	Setze $A_K=50{,}24\text{cm}^2$ ein.
	$=$	$\displaystyle \sqrt{\dfrac{50{,}24\;\text{cm}^2}{\pi}}$
	↓	$\pi\approx 3{,}14$
	$\approx ≈$	$\displaystyle \sqrt{\dfrac{50{,}24\;\text{cm}^2}{3{,}14}}$
	$=$	$\displaystyle \sqrt{16\;\text{cm}^2}$
	$=$	$\displaystyle 4\;\text{cm}$

Antwort: Der Radius des Grundkreises beträgt etwa $r=4\;\text{cm}$ .

Berechnung der Höhe des Zylinders

Du kennst den Wert der Mantelfläche $A_{M}$ und du kennst die Formel für die Berechnung der Mantelfläche $A_{M}$ des Zylinders (Nr. 2). Sie enthält die gesuchte Höhe $h$ und den gerade berechneten Grundkreisradius $r$ .

$\displaystyle A_M$	$=$	$\displaystyle 2\cdot r \cdot \pi \cdot h$	$\displaystyle :(2\cdot r\cdot\pi)$
	↓	Löse nach $h$ auf.
$\displaystyle \dfrac{A_M}{2\cdot r\cdot\pi}$	$=$	$\displaystyle h$
	↓	Setze $A_M=251{,}2\text{cm}^2$ und $r=4\text{cm}$ ein.
$\displaystyle h$	$=$	$\displaystyle \dfrac{251{,}2 \;\text{cm}^2}{2\cdot 4\;\text{cm}\cdot\pi}$
	↓	$\pi\approx 3{,}14$
	$\approx ≈$	$\displaystyle \dfrac{251{,}2 \;\text{cm}^2}{2\cdot 4\;\text{cm}\cdot3{,}14}$
	$=$	$\displaystyle \dfrac{251{,}2 \;\text{cm}^2}{25{,}12\;\text{cm}}$
	$=$	$\displaystyle 10\;\text{cm}$

Antwort: Der Zylinder hat eine Höhe von etwa $h=10\;\text{cm}$ .

Berechnung des Zylindervolumens

Du kennst die Formel für das Zylindervolumen $V_{Zyl}$ (Nr. 4). Sie enthält den berechneten Grundkreisflächeninhalt $A_{K}$ und die gerade berechnete Höhe $h$ .

$\displaystyle V_{Zyl}$	$=$	$\displaystyle A_K\cdot h$
	↓	Setze $A_K=50{,}24\text{m}^2$ und $h=10\text{cm}$ ein.
	$=$	$\displaystyle 50{,}24\;\text{cm}^2\cdot 10 \;\text{cm}$
	$=$	$\displaystyle 502{,}4\;\text{cm}^3$

Antwort: Der Zylinder hat ein Volumen von etwa $502{,}4\; \text{cm}^3$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Gegeben sind die Mantelfläche $A_M = 571{,}48 \;\text{cm}^2$ und die Fläche des Grundkreises $A_K= 153{,}86\;\text{cm}^2$ .

Berechne den Radius $r$ des Grundkreises, die Höhe $h$ und den Oberflächeninhalt $O_{Zyl}$ des Zylinders.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder

Gegeben: Mantelfläche $A_{M}$ und Fläche des Grundkreises $A_{K}$

Gesucht: Radius $r$ des Grundkreises, Höhe $h$ des Zylinders, Oberflächeninhalt $O_{Zyl}$ und das Volumen $V_{Zyl}$

Benötigte Formeln:

Oberfläche des Zylinders : $O_{Zyl}=2\cdot A_K+A_M$
Mantelfläche des Zylinders: $A_M=2\cdot r \cdot \pi \cdot h $
Fläche des Grundkreises: $A_K=r^2\cdot\pi$
Volumen des Zylinders: $V_{Zyl}=A_K \cdot h$ oder $V_{Zyl}=r^2 \cdot \pi \cdot h$

Radius der Grundkreisfläche

Du kennst die Formel für die Grundkreisfläche $A_{K}$ des Zylinders (Nr. 3). Benutze sie, um den Radius $r$ zu berechnen.

$\displaystyle A_K$	$=$	$\displaystyle r^2\cdot \pi$	$\displaystyle :\pi$
	↓	Löse nach $r$ auf.
$\displaystyle \dfrac{A_K}{\pi}$	$=$	$\displaystyle r^2$	$\displaystyle \sqrt{}$
$\displaystyle r$	$=$	$\displaystyle \sqrt{\dfrac{A_K}{\pi}}$
	↓	Setze $A_K=153{,}86\text{cm}^2$ ein.
	$=$	$\displaystyle \sqrt{\dfrac{153{,}86\;\text{cm}^2}{\pi}}$
	↓	$\pi\approx 3{,}14$
	$\approx ≈$	$\displaystyle \sqrt{\dfrac{153{,}86\;\text{cm}^2}{3{,}14}}$
	$=$	$\displaystyle \sqrt{49\;\text{cm}^2}$
	$=$	$\displaystyle 7\;\text{cm}$

Antwort: Der Radius des Grundkreises beträgt etwa $r=7\;\text{cm}$ .

Berechnung der Höhe des Zylinders

$\displaystyle A_M$	$=$	$\displaystyle 2\cdot r \cdot \pi \cdot h$	$\displaystyle :(2\cdot r\cdot\pi)$
	↓	Löse nach $h$ auf.
$\displaystyle \dfrac{A_M}{2\cdot r\cdot\pi}$	$=$	$\displaystyle h$
	↓	Setze $A_M=571{,}48\text{cm}^2$ und $r=7\text{cm}$ ein
$\displaystyle h$	$=$	$\displaystyle \dfrac{571{,}48 \;\text{cm}^2}{2\cdot 7\;\text{cm}\cdot\pi}$
	↓	$\pi\approx 3{,}14$
	$\approx ≈$	$\displaystyle \dfrac{571{,}48 \;\text{cm}^2}{2\cdot 7\;\text{cm}\cdot3{,}14}$
	$=$	$\displaystyle \dfrac{571{,}48 \;\text{cm}^2}{43{,}96\;\text{cm}}$
	$=$	$\displaystyle 13\;\text{cm}$

Antwort: Der Zylinder hat eine Höhe von etwa $h=13\;\text{cm}$ .

Berechnung des Oberflächeninhalts des Zylinders

Du kennst den Wert der Grundkreisfläche $A_{K}$ und du kennst den Wert der Mantelfläche $A_{M}$ des Zylinders. Berechne mit Formel Nr. 1 den Oberflächeninhalt $O_{Zyl}$ des Zylinders.

$\displaystyle O_{Zyl}$	$=$	$\displaystyle 2\cdot A_K+A_M$
	↓	Setze $A_K=153{,}86\text{cm}^2$ und $A_M=571{,}48\text{cm}^2$ ein.
	$=$	$\displaystyle 2\cdot 153{,}86 \;\text{cm}^2+571{,}48\;\text{cm}^2$
	$=$	$\displaystyle 307{,}72\;\text{cm}^2+571{,}48\;\text{cm}^2$
	$=$	$\displaystyle 879{,}2\;\text{cm}^2$

Antwort: Der Zylinder hat einen Oberflächeninhalt von etwa $879{,}2\;\text{cm}^2$ .

Berechnung des Zylindervolumens

Du kennst die Formel für das Zylindervolumen $V_{Zyl}$ (Nr. 4). Sie enthält den gegebenen Wert für den Grundkreisflächeninhalt $A_{K}$ und die gerade berechnete Höhe $h$ .

$\displaystyle V_{Zyl}$	$=$	$\displaystyle A_K\cdot h$
	↓	Setze $A_K=153{,}86\text{cm}^2$ und $h=13\text{cm}$ ein.
	$=$	$\displaystyle 153{,}86\;\text{cm}^2\cdot 13 \;\text{cm}$
	$=$	$\displaystyle 2000{,}18\;\text{cm}^3$

Antwort: Der Zylinder hat ein Volumen von etwa $2000{,}18\; \text{cm}^3$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Gegeben sind der Oberflächeninhalt $O_{Zyl} = 2788{,}32\;\text{cm}^2$ und die Fläche des Grundkreises $A_K= 452{,}16\;\text{cm}^2$ . Berechne den Radius $r$ des Grundkreises, die Mantelfläche $A_{M}$ und die Höhe $h$ des Zylinders.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder

Gegeben: Oberflächeninhalt $O_{Zyl}$ und Fläche des Grundkreises $A_{K}$

Gesucht: Radius $r$ des Grundkreises, die Mantelfläche $A_{M}$ , die Höhe $h$ des Zylinders und das Volumen $V_{Zyl}$

Benötigte Formeln:

Oberfläche des Zylinders : $O_{Zyl}=2\cdot A_K+A_M$
Mantelfläche des Zylinders: $A_M=2\cdot r \cdot \pi \cdot h $
Fläche des Grundkreises: $A_K=r^2\cdot\pi$
Volumen des Zylinders: $V_{Zyl}=A_K \cdot h$ oder $V_{Zyl}=r^2 \cdot \pi \cdot h$

Radius der Grundkreisfläche

Du kennst die Formel für die Grundkreisfläche $A_{K}$ des Zylinders (Nr. 3). Benutze sie, um den Radius $r$ zu berechnen.

$\displaystyle A_K$	$=$	$\displaystyle r^2\cdot \pi$	$\displaystyle :\pi$
	↓	Löse nach $r$ auf.
$\displaystyle \dfrac{A_K}{\pi}$	$=$	$\displaystyle r^2$	$\displaystyle \sqrt{}$
$\displaystyle r$	$=$	$\displaystyle \sqrt{\dfrac{A_K}{\pi}}$
	↓	Setze $A_K=452{,}16\text{cm}^2$ ein.
	$=$	$\displaystyle \sqrt{\dfrac{452{,}16\;\text{cm}^2}{\pi}}$
	↓	$\pi\approx 3{,}14$
	$\approx ≈$	$\displaystyle \sqrt{\dfrac{452{,}16\;\text{cm}^2}{3{,}14}}$
	$=$	$\displaystyle \sqrt{144\;\text{cm}^2}$
	$=$	$\displaystyle 12\;\text{cm}$

Antwort: Der Radius des Grundkreises beträgt etwa $r=12\;\text{cm}$ .

Berechnung der Mantelfläche des Zylinders

Du kennst den Wert des Oberflächeninhalts $O_{Zyl}$ und du kennst den Wert der Grundkreisfläche $A_{K}$ des Zylinders. Berechne mit Formel Nr. 1 die Mantelfläche $A_{M}$ des Zylinders.

$\displaystyle O_{Zyl}$	$=$	$\displaystyle 2\cdot A_K+A_M$	$\displaystyle -2\cdot A_K$
	↓	Löse nach $A_{M}$ auf.
$\displaystyle O_{Zyl}-2\cdot A_K$	$=$	$\displaystyle A_M$
	↓	Setze $O_{Zyl}=2788{,}32\text{cm}^2$ und $A_K=452{,}16\text{cm}^2$ ein.
$\displaystyle A_M$	$=$	$\displaystyle 2788{,}32\;\text{cm}^2-2\cdot 452{,}16 \;\text{cm}^2$
	$=$	$\displaystyle 2788{,}32\;\text{cm}^2-904{,}32\;\text{cm}^2$
	$=$	$\displaystyle 1884\;\text{cm}^2$

Antwort: Der Zylinder hat eine Mantelfläche von etwa $1884\; \text{cm}^2$ .

Berechnung der Höhe des Zylinders

Du hast den Wert der Mantelfläche $A_{M}$ und den Grundkreisradius $r$ berechnet. Mit Formel Nr. 2 kannst du die gesuchte Höhe $h$ berechnen.

$\displaystyle A_M$	$=$	$\displaystyle 2\cdot r \cdot \pi \cdot h$	$\displaystyle :(2\cdot r\cdot\pi)$
	↓	Löse nach $h$ auf.
$\displaystyle \dfrac{A_M}{2\cdot r\cdot\pi}$	$=$	$\displaystyle h$
	↓	Setze $A_M=1884\text{cm}^2$ und $r=12\text{cm}$ ein.
$\displaystyle h$	$=$	$\displaystyle \dfrac{1884 \;\text{cm}^2}{2\cdot 12\;\text{cm}\cdot\pi}$
	↓	$\pi\approx 3{,}14$
	$\approx ≈$	$\displaystyle \dfrac{1884 \;\text{cm}^2}{2\cdot 12\;\text{cm}\cdot3{,}14}$
	$=$	$\displaystyle \dfrac{1884 \;\text{cm}^2}{75{,}36\;\text{cm}}$
	$=$	$\displaystyle 25\;\text{cm}$

Antwort: Der Zylinder hat eine Höhe von etwa $h=25\;\text{cm}$ .

Berechnung des Zylindervolumens

Du kennst die Formel für das Zylindervolumen $V_{Zyl}$ (Nr. 4). Sie enthält den gegebenen Wert für den Grundkreisflächeninhalt $A_{K}$ und die gerade berechnete Höhe $h$ .

$\displaystyle V_{Zyl}$	$=$	$\displaystyle A_K\cdot h$
	↓	Setze $A_K=452{,}16\text{cm}^2$ und $h=25\text{cm}$ ein.
	$=$	$\displaystyle 452{,}16\;\text{cm}^2\cdot 25 \;\text{cm}$
	$=$	$\displaystyle 11304\;\text{cm}^3$

Antwort: Der Zylinder hat ein Volumen von etwa $11304\; \text{cm}^3$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

15
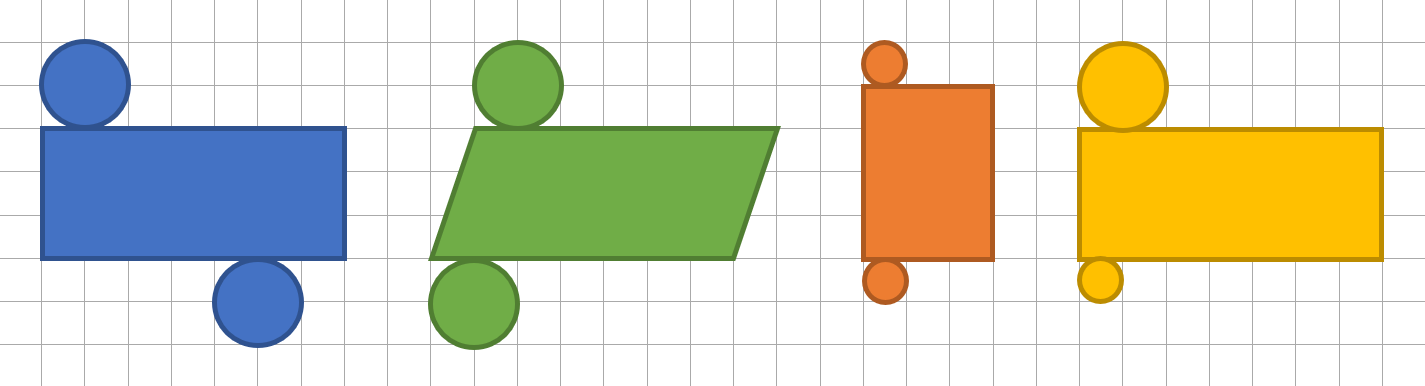
Wähle alle Bilder aus, die ein Zylindernetz darstellen?
Bild 1
Bild 2
Bild 3
Bild 4
Bild 5
Bild 6
Bild 7
Für diese Aufgabe benötigst Du folgendes Grundwissen: Körpernetze
Bild 1
Antwort: Kein Zylindernetz
In diesem Bild ist die das Rechteck länger als der Umfang der Kreise. Die Länge der einen Mantelseite (an der sich die Kreise befinden) ist etwa vier mal so groß wie der Durchmesser $d$ des Kreises. Der Kreis passt somit in ein Quadrat mit der Seitenläge $d$ . Anschaulich ist klar, dass der Umfang des Quadrates größer als der Kreisumfang ist. Deshalb kann es kein Zylindernetz sein.
Bild 2
Antwort: Kein Zylindernetz
Der Umfang des Grund-(Deck) Kreises ist viel größer als die Länge der Seite an der sich die Kreise befinden. Deshalb kann es kein Zylindernetz sein.
Bild 3
Antwort: Zylindernetz
Hier entspricht die Länge der Rechteckseite an der sich die Kreise befinden dem Kreisumfang. Die Kreise sind an zwei gegenüberliegenden Rechteckseiten angeordnet. Deshalb ist es ein Zylindernetz.
Bild 4
Antwort: Kein Zylindernetz
Die Kreise müssen an zwei gegenüberliegenden Rechteckseiten angeordnet sein. Hier sind sie auf einer Seite angeordnet. Deshalb kann es kein Zylindernetz sein.
Bild 5
Antwort: Zylindernetz
Hier entspricht die Länge der Rechteckseite an der sich die Kreise befinden dem Kreisumfang. Die beiden Kreise liegen zudem an zwei gegenübberliegenden Rechtecksseiten. Deshalb ist es ein Zylindernetz.
Bild 6
Antwort: Kein Zylindernetz
Die beiden Kreise haben verschiedene Radien (Grund-und Deckkreis müssen deckungsgleich sein).
Deshalb kann es kein Zylindernetz sein.
Bild 7
Antwort: Kein Zylindernetz
Die Kreise schneiden die Mantelfläche. Die Kreise dürfen nur einen gemeinsamen Berührpunkt mit der Mantelfläche haben. Deshalb kann es kein Zylindernetz sein.

Zeichne jeweils ein Schrägbild und ein Netz der gegebenen stehenden geraden Kreiszylinder.

Berechne außerdem jeweils die Oberfläche.

Der Kreiszylinder hat einen Durchmesser von $5\;\text{cm}$ und eine Höhe von $5\;\text{cm}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder zeichnen

Schrägbild

1. Zeichne den Durchmesser $\text{d}=2\cdot\text{r}= 5\;\text{cm}$ des Zylinders (gestrichelt).

2. Zeichne eine Mittelsenkrechte mit der Länge $\text{r}=\dfrac{d}{2}=2{,}5\;\text{cm}$ (gestrichelt), so wie in der nebenstehenden Abbildung.

3. Ein Kreis in perspektivischer Darstellung erscheint als Ellipse. Zeichne um die Enden der beiden Strecken eine Ellipse.

Der nicht sichtbare Teil der Grundfläche $G$ (der hintere Rand der Ellipse) wird gestrichelt gezeichnet.

4. Zeichne die seitlichen Begrenzungslinien des Zylinders senkrecht an die Enden des Durchmessers mit einer Länge von $\text{h}=5\;\text{cm}$ .

5. Zeichne die Deckfläche ebenfalls als Ellipse parallel zur Grundfläche.

Netz

Der abgewickelte Mantel des Zylinders ist ein Rechteck. Die Länge $a$ des Rechtecks entspricht dem Umfang $U$ des Grund-(Deck) Kreises. Die Breite $b$ des Rechtecks entspricht der Höhe $h$ des Zylinders.

$a=2\cdot r\cdot \pi\approx 2\cdot 2{,}5\;\text{cm}\cdot3{,}14=15{,}7\;\text{cm}$

$b=5\;\text{cm}$

Zeichne ein Rechteck mit den Seitenlängen $a=15{,}7\;\text{cm}$ und $b=5\;\text{cm}$ .

Auf den zwei gegenüberliegenden Rechteckseiten $a$ kannst du je einen Kreis mit dem Radius $r=2{,}5\;\text{cm}$ zeichnen. Die Kreise müssen direkt an der Rechteckfläche anliegen.

Oberfläche

Die Oberfläche des Zylinders besteht aus zwei flächengleichen Kreisen (Grundfläche und Deckfläche) und der Mantelfläche (Rechteck):

$\displaystyle O_{Zyl}$	$=$	$\displaystyle 2\cdot A_{Kreis}+A_{Mantel}$
	$=$	$\displaystyle 2\cdot r^2\cdot \pi+2\cdot r\cdot \pi\cdot h$
	$=$	$\displaystyle 2\cdot (2{,}5\;\text{cm})^2\cdot \pi+2\cdot (2{,}5\;\text{cm})\cdot \pi\cdot (5\;\text{cm})$
	$=$	$\displaystyle 12{,}5\;\text{cm}^2\cdot \pi+25\;\text{cm}^2\cdot \pi$
	$=$	$\displaystyle 37{,}5\;\text{cm}^2\cdot \pi$
	$\approx ≈$	$\displaystyle 117{,}8\;\text{cm}^2$

Antwort: Die Oberfläche des Zylinders beträgt etwa $117{,}8\;\text{cm}^2$ .

Anmerkung : Wird mit $\pi \approx 3{,}14$ gerechnet, erhältst du für die Oberfläche gerundet ebenfalls $117{,}8\;\text{cm}^2$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Der Kreiszylinder hat einen Durchmesser von $9\;\text{cm}$ und eine Höhe von $8\;\text{cm}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder zeichnen

Schrägbild

1. Zeichne den Durchmesser $\text{d}=2\cdot\text{r}= 9\;\text{cm}$ des Zylinders (gestrichelt).

2. Zeichne eine Mittelsenkrechte mit der Länge $\text{r}=\dfrac{d}{2}=4{,}5\;\text{cm}$ (gestrichelt), so wie in der nebenstehenden Abbildung.

3. Ein Kreis in perspektivischer Darstellung erscheint als Ellipse. Zeichne um die Enden der beiden Strecken eine Ellipse.

Der nicht sichtbare Teil der Grundfläche $G$ (der hintere Rand der Ellipse) wird gestrichelt gezeichnet.

4. Zeichne die seitlichen Begrenzungslinien des Zylinders senkrecht an die Enden des Durchmessers mit einer Länge von $\text{h}=8\;\text{cm}$ .

5. Zeichne die Deckfläche ebenfalls als Ellipse parallel zur Grundfläche.

Netz

$a=2\cdot r\cdot \pi\approx 2\cdot 4{,}5\;\text{cm}\cdot3{,}14\approx 28{,}3\;\text{cm}$

$b=8\;\text{cm}$

Zeichne ein Rechteck mit den Seitenlängen $a=28{,}3\;\text{cm}$ und $b=8\;\text{cm}$ .

Auf den zwei gegenüberliegenden Rechteckseiten $a$ kannst du je einen Kreis mit dem Radius $r=4{,}5\;\text{cm}$ zeichnen. Die Kreise müssen direkt an der Rechteckfläche anliegen.

Oberfläche

Die Oberfläche des Zylinders besteht aus zwei flächengleichen Kreisen (Grundfläche und Deckfläche) und der Mantelfläche (Rechteck):

$\displaystyle O_{Zyl}$	$=$	$\displaystyle 2\cdot A_{Kreis}+A_{Mantel}$
	$=$	$\displaystyle 2\cdot r^2\cdot \pi+2\cdot r\cdot \pi\cdot h$
	$=$	$\displaystyle 2\cdot (4{,}5\;\text{cm})^2\cdot \pi+2\cdot (4{,}5\;\text{cm})\cdot \pi\cdot (8\;\text{cm})$
	$=$	$\displaystyle 40{,}5\;\text{cm}^2\cdot \pi+72\;\text{cm}^2\cdot \pi$
	$=$	$\displaystyle 112{,}5\;\text{cm}^2\cdot \pi$
	$\approx ≈$	$\displaystyle 353{,}4\;\text{cm}^2$

Antwort: Die Oberfläche des Zylinders beträgt etwa $353{,}4\;\text{cm}^2$ .

Anmerkung : Wird mit $\pi \approx 3{,}14$ gerechnet, erhältst du für die Oberfläche etwa $353{,}3\;\text{cm}^2$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zum Zylinder

Netz blau

Netz grün

Netz orange

Netz gelb

Berechnung der Grundkreisfläche

Berechnung des Radius der Grundkreisfläche

Berechnung der Höhe des Zylinders

Berechnung des Zylindervolumens

Hast du eine Frage oder Feedback?

Radius der Grundkreisfläche

Berechnung der Höhe des Zylinders

Berechnung des Oberflächeninhalts des Zylinders

Berechnung des Zylindervolumens

Hast du eine Frage oder Feedback?

Radius der Grundkreisfläche

Berechnung der Mantelfläche des Zylinders

Berechnung der Höhe des Zylinders

Berechnung des Zylindervolumens

Hast du eine Frage oder Feedback?

Bild 1

Bild 2

Bild 3

Bild 4

Bild 5

Bild 6

Bild 7

Schrägbild

Netz

Oberfläche

Hast du eine Frage oder Feedback?

Schrägbild

Netz

Oberfläche

Hast du eine Frage oder Feedback?