Aufgaben zum Strahlensatz oder Vierstreckensatz

Betrachte die Figur rechts, in der die Geraden durch $D E$ und $B C$ zueinander parallel sind. $\;$ Es gilt: $|\overline{AB}| = 8 \;\text{cm}$ , $|\overline{BC}|= 5 \;\text{cm}$ und $|\overline{DE}| = 3\; \text{cm}$ .

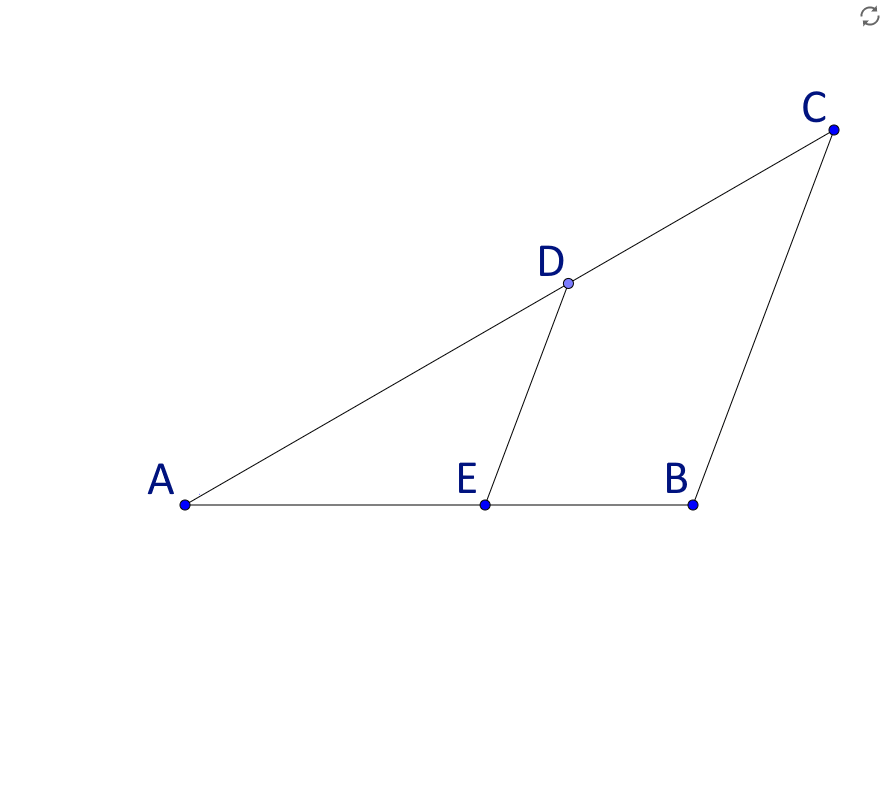
Wie lang ist die Strecke $\left|\overline{EB}\right|$ in $\text{cm}$ ?

Wenn gilt $|\overline{CD}| = 4 \;\text{cm}$ , wie lange ist dann $\left|\overline{AC}\right|$ in $\text{cm}$ ?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Strahlensatz

Es gibt zwei Möglichkeiten, $|\overline{AC}|$ aus den gegebenen Streckenlängen zu berechnen.

Möglichkeit A aus den ursprünglichen Angaben zu $|\overline{BC}|$ , $|\overline{DE}|$ und $|\overline{CD}|$ :

$\displaystyle \left\|\overline{AC}\right\|$	$=$	$\displaystyle \mathbf{\|\overline{AD}\|}+\|\overline{DC}\|\:(1)$
	↓	Die Strecke $\|\overline{AC}\|$ ist die Summe aus den Strecken $\|\overline{AD}\|$ (unbekannt) und $\|\overline{CD}\|$ (gegeben).
$\displaystyle \frac{\|\overline{AD}\|}{\|\overline{AC}\|}$	$=$	$\displaystyle \frac{\|\overline{DE}\|}{\|\overline{BC}\|}$	$\displaystyle \cdot\|\overline{AC}\|$
	↓	Aus dem Strahlensatz kannst du außerdem das Verhältnis zwischen $\|\overline{AC}\|$ und $\|\overline{AD}\|$ berechnen.
$\displaystyle \|\overline{AD}\|$	$=$	$\displaystyle \frac{\|\overline{DE}\|}{\|\overline{BC}\|}\cdot\|\overline{AC}\|$
	$=$	$\displaystyle \frac{3\:cm}{5\:cm}\cdot\|\overline{AC}\|$
	$=$	$\displaystyle 0.6\:\|\overline{AC}\|$

$\displaystyle \|\overline{AC}\|$	$=$	$\displaystyle 0.6\:\|\overline{AC}\|+\|\overline{DC}\|$	$\displaystyle -0.6\:\|\overline{AC}\|$
$\displaystyle 0.4\:\|\overline{AC}\|$	$=$	$\displaystyle \|\overline{DC}\|$	$\displaystyle :0.4 \:oder \cdot\:2.5$
$\displaystyle \|\overline{AC}\|$	$=$	$\displaystyle 2.5\cdot\|\overline{DC}\|$
	$=$	$\displaystyle 2.5\cdot4\:cm$
	$=$	$\displaystyle \mathbf{10\:cm}$

Die Strecke $\overline{AC}$ ist also 10 cm lang.

Alternativ kannst du $|\overline{AC}|$ auch aus $|\overline{AB}|$ , $|\overline{CD}|$ und $|\overline{EB}|$ aus der vorigen Aufgabe berechnen:

$\displaystyle \frac{\|\overline{CD}\|}{\mathbf{\|\overline{AC}\|}}$	$=$	$\displaystyle \frac{\|\overline{EB}\|}{\|\overline{AB}\|}$
	↓	Aus dem Strahlensatz ergibt sich das Verhältnis von $\|\overline{CD}\|$ und $\|\overline{AC}\|$ aus $\|\overline{EB}\|$ und $\|\overline{AB}\|$ . Drehe den Bruch auf beiden Seiten um.
$\displaystyle \frac{\|\overline{AC}\|}{\|\overline{CD}\|}$	$=$	$\displaystyle \frac{\|\overline{AB}\|}{\|\overline{EB}\|}$	$\displaystyle \cdot\|\overline{CD}\|$
$\displaystyle \|\overline{AC}\|$	$=$	$\displaystyle \frac{\|\overline{AB}\|}{\|\overline{EB}\|}\cdot\|\overline{CD}\|$
	$=$	$\displaystyle \frac{8\:cm}{3.2\:cm}\cdot4\:cm$
	$=$	$\displaystyle \mathbf{10\:cm}$
	↓	Die Strecke $\overline{AC}$ ist also 10 cm lang.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \frac{\overline{AE}}{\overline{AB}}$	$=$	$\displaystyle \frac{\overline{DE}}{\overline{BC}}$	$\displaystyle \cdot\overline{AB}$
$\displaystyle \overline{AE}$	$=$	$\displaystyle \frac{\overline{DE}}{\overline{BC}}\cdot\overline{AB}$
	$=$	$\displaystyle \frac{3\:cm}{5\:cm}\cdot8\:cm$
	$=$	$\displaystyle \mathbf{4{,}8\:cm}$
	↓	$4.8 c m$ einsetzen in $(1)$ .

$\displaystyle \left\|\overline{AC}\right\|$	$=$	$\displaystyle \mathbf{\|\overline{AD}\|}+\|\overline{DC}\|\:(1)$
	↓	Die Strecke $\|\overline{AC}\|$ ist die Summe aus den Strecken $\|\overline{AD}\|$ (unbekannt) und $\|\overline{CD}\|$ (gegeben).
$\displaystyle \frac{\|\overline{AD}\|}{\|\overline{AC}\|}$	$=$	$\displaystyle \frac{\|\overline{DE}\|}{\|\overline{BC}\|}$	$\displaystyle \cdot\|\overline{AC}\|$
	↓	Aus dem Strahlensatz kannst du außerdem das Verhältnis zwischen $\|\overline{AC}\|$ und $\|\overline{AD}\|$ berechnen.
$\displaystyle \|\overline{AD}\|$	$=$	$\displaystyle \frac{\|\overline{DE}\|}{\|\overline{BC}\|}\cdot\|\overline{AC}\|$
	$=$	$\displaystyle \frac{3\:cm}{5\:cm}\cdot\|\overline{AC}\|$
	$=$	$\displaystyle 0.6\:\|\overline{AC}\|$