1 Kursübersicht
Inhalt
In diesem Kurs lernst du, was eine Lösungsmenge ist, wie viele Lösungen es bei einem Linearen Gleichungssystem (LGS) geben kann und welche weiteren Lösungsverfahren es neben dem Gleichsetzungsverfahren noch gibt.
Vorkenntnisse
Du solltest schon wissen, was ein Schnittpunkt ist und wie man ihn sowohl graphisch als auch rechnerisch bestimmt. Außerdem musst du für diesen Kurs wissen, was ein LGS ist.
Falls du etwas davon noch nicht weißt, schau dir doch zuerst den ersten Teil des Einführungskurses zu linearen Gleichungssystemen an.
Kursdauer
Dieser Kurs dauert ca. 2 Stunden.
2 Die Geburtstagsfeier von Tinas Eltern
Tinas Eltern feiern dieses Jahr gemeinsam ihren Geburtstag.
Tina hat ein schlechtes Gewissen, denn sie hat vergessen, wie alt die beiden sind!

Ihr Vater sagt:
"Wenn du mein Alter verdoppelst und zu dem Alter deiner Mutter die Hälfte ihres Alters dazu addierst, ergibt das zusammen 150 Jahre."
Das hat Tina nicht sonderlich geholfen.
Ihre Mutter sagt:
"Wenn du zu meinem Alter drei Jahre dazu rechnest und von dem deines Vaters zwei Jahre abziehst, sind wir gleich alt!"
Tina nimmt zur Zeit in der Schule Gleichungssysteme durch und will nun versuchen, damit das Alter der Eltern zu ermitteln. Sie rennt los und holt Stift und Block. Jetzt kann sie ausrechnen, wie alt ihre Eltern sind. Probier's doch mal selbst!
3 Wiederholung: LGS, Gleichsetzungsverfahren
Um das Alter von Tinas Eltern zu erfahren, ist es nützlich, dass du dir das LGS und das Gleichsetzungsverfahren ins Gedächtnis rufst.
Was ist ein LGS?
Ein lineares Gleichungssystem hatte bisher oft zwei Gleichungen der Form , mit den Unbekannten und .
Die Lösung des LGS hast du als Schnittpunkt dieser Geraden kennengelernt.
Lösung mithilfe des Gleichsetzungsverfahrens
Die Anwendung des Gleichsetzungsverfahrens ist bereits in seinem Namen versteckt. Das Stichwort ist das Gleichsetzen von Gleichungen. Dafür musst du wie folgt vorgehen:
Löse die Gleichungen des Gleichungssystems jeweils nach derselben Unbekannten auf.
Setze die Gleichungen gleich.
Löse die entstandene Gleichung nach der verbliebenen Unbekannten auf.
Setze diese Variable in eine der ursprünglichen Gleichungen ein.
4 Das Alter der Eltern als Gleichungen
Tinas Eltern haben ihr gute Hinweise gegeben, um zwei Gleichungen aufzustellen.
Vater: "Wenn du mein Alter verdoppelst und zu dem Alter deiner Mutter die Hälfte ihres Alters dazu addierst, ergibt das zusammen 150 Jahre."
Zunächst legt Tina die Variablen fest.
Alter der Mutter
Alter des Vaters
Aus der Aussage des Vaters bekommt Tina die erste Gleichung:
Verdopple das Alter des Vaters:
Zähle zu dem Alter der Mutter die Hälfte dazu:
Mutter:"Wenn du zu meinem Alter drei Jahre dazu rechnest und von dem deines Vaters zwei Jahre abziehst, sind wir gleich alt!"
Zu dem Alter der Mutter addieren:
Vom Alter des Vaters abziehen:
5 Lösungsmenge
Mit Geraden haben die beiden Gleichungen von Tinas Eltern nicht mehr viel zu tun!
Auch wenn du sie so umformen kannst, dass man sie zeichnen kann, ist das im Sachzusammenhang nicht sehr anschaulich.
Deshalb gibt man die Lösung bei vielen Aufgaben nicht als Schnittpunkt, sondern mit einem Antwortsatz und/oder als Lösungsmenge an:
Hat man zum Beispiel ein System, das für die Werte und gelöst wird, so schreibst du:
Wenn du die Variablen nach dem Alphabet sortierst, kannst du auch die letzte Schreibweise, die Kurzschreibweise, verwenden.
6 Wie viele Lösungen gibt es? (1/2)
Wenn du ein lineares Gleichungssystem löst, können Fälle auftreten:
Du stößt bei der Berechnung der Lösung auf eine falsche Aussage (z. B. ).
Du stellst beim Umformen fest, dass die Gleichungen identisch sind. Es ergibt sich eine Aussage, die wahr ist, egal welche Zahl du einsetzt (z. B. ).
Beim Berechnen der Lösung erhältst du für die Gleichungen des Systems eine eindeutige Variablenbelegung (z. B. und ). Dies ist der bereits bekannte Normalfall!
Panik! Was tun bei 1. und 2.?
Keine Sorge! Auch lineare Gleichungssysteme können nicht immer perfekt sein. :-) Es gibt Arten von Systemen: Welche mit , oder Lösungen.
7 Wie viele Lösungen gibt es? (2/2)
Wie findet man heraus, welche Art von Gleichungssystem es ist?
Die drei verschiedenen Arten von Gleichungssystemen werden anhand von Beispielen erklärt.
Fall 1: keine Lösung
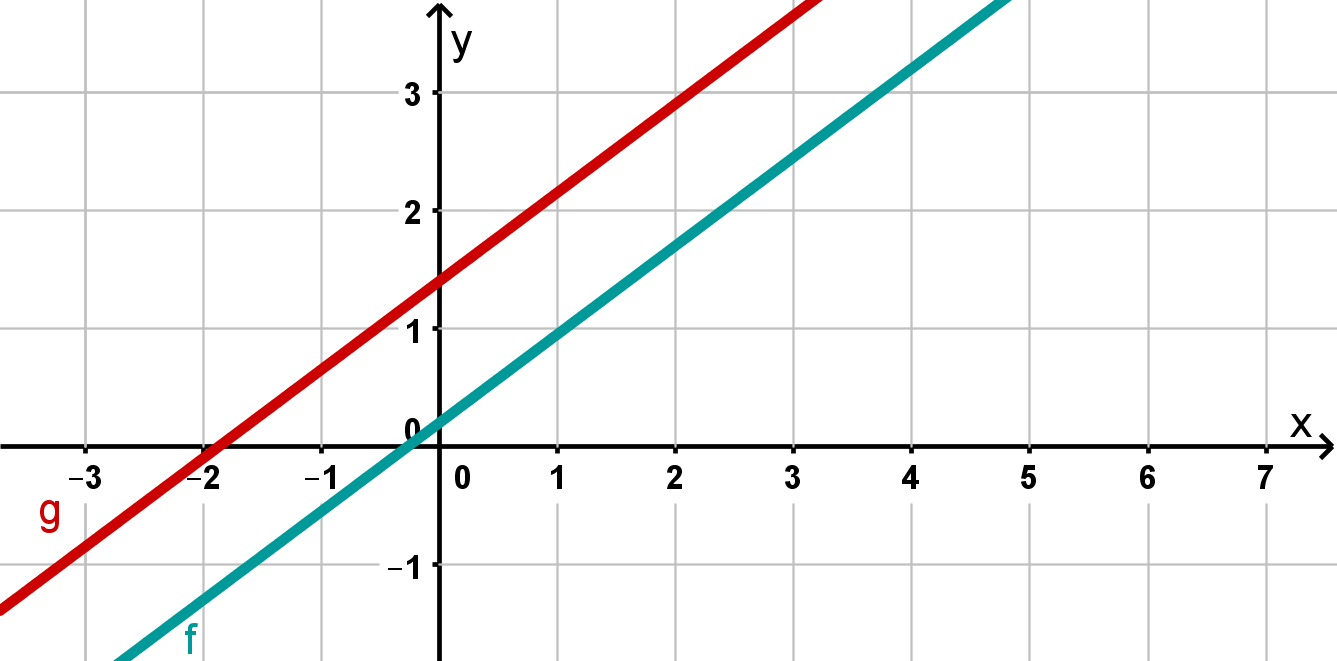
In der Grafik siehst du zwei parallele Geraden. Dies kannst du auch daran erkennen, dass sie dieselbe Steigung, nämlich , aber unterschiedliche -Achsenabschnitte haben. Die Geraden schneiden sich nie, es gibt also keine Lösung. In diesem Fall ist die Lösungsmenge die leere Menge: oder .
Fall 2: eine Lösung
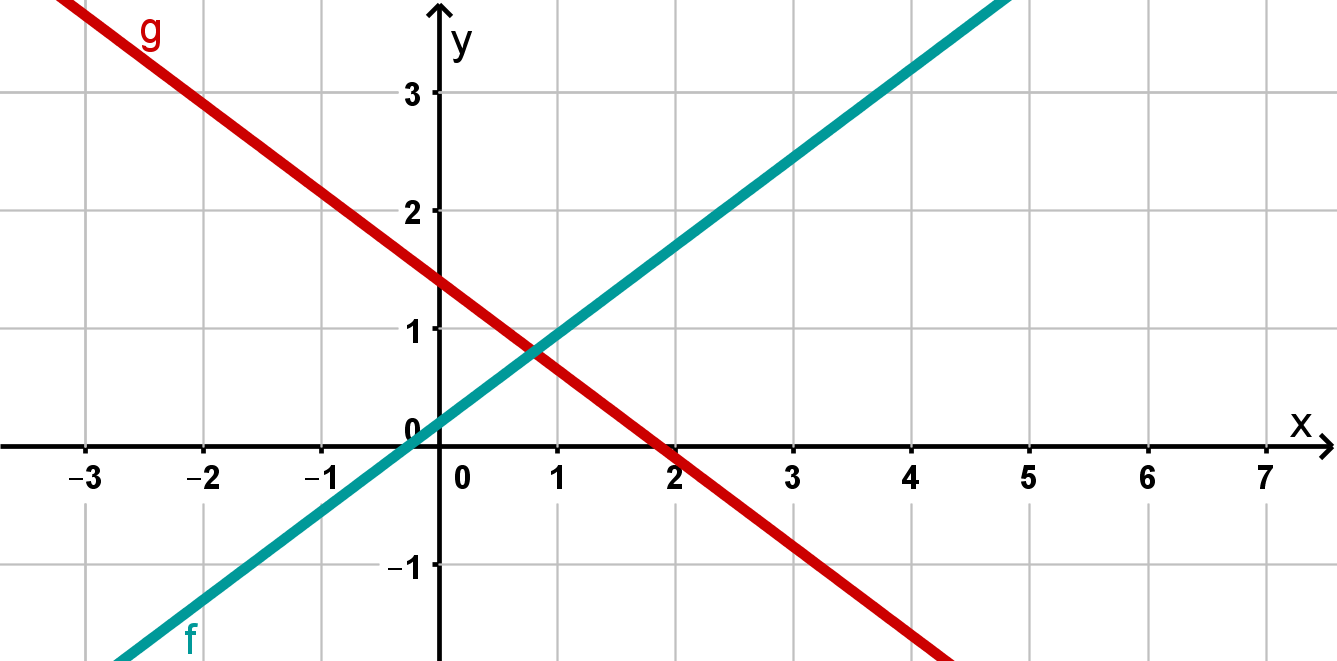
Anhand der Grafik kannst du erkennen, dass die Geraden sich in einem Schnittpunkt kreuzen. Dies ist immer der Fall, wenn beide Geraden unterschiedliche Steigungen haben. Es gibt also genau eine Lösung. Die Lösungsmenge hier ist einfach wieder dein Zahlenpaar .
Fall 3: unendlich viele Lösungen
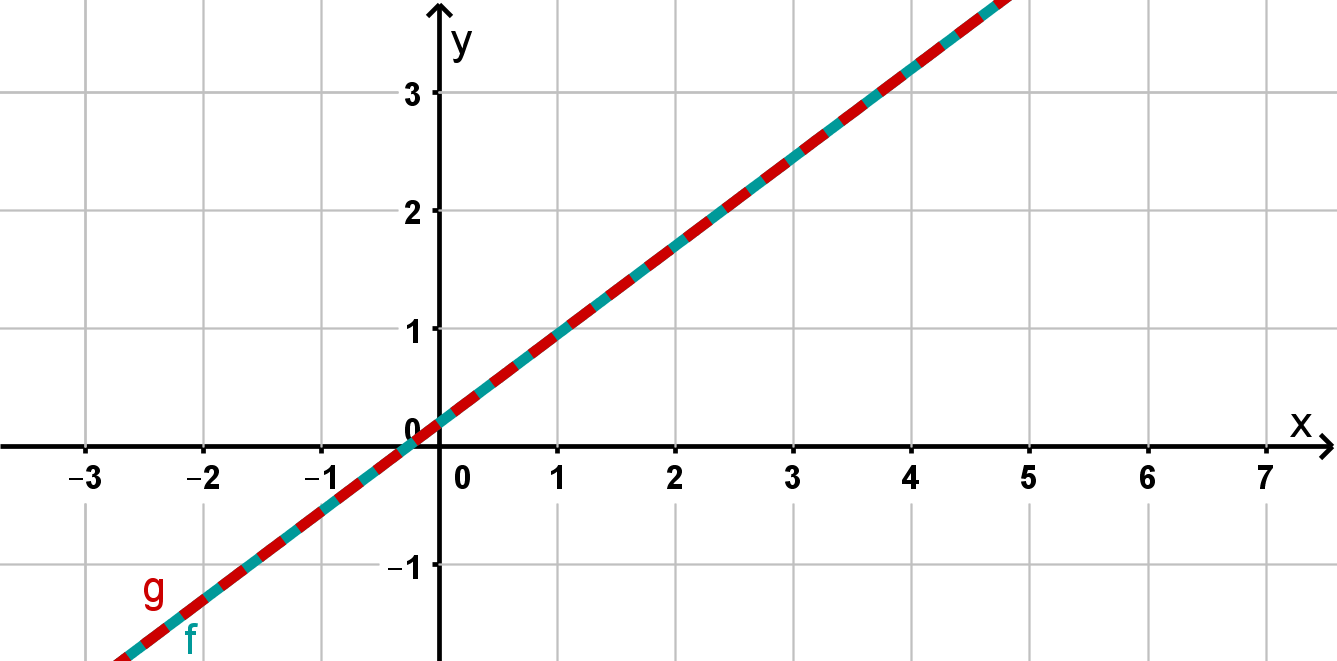
Formst du beide Gleichungen um, erkennst du, dass beide Geraden dieselbe Steigung und denselben -Achsenabschnitt haben. Sie sind also identisch. Jeder Punkt auf den Geraden ist ein Schnittpunkt. Es gibt also unendlich viele Lösungen. Die Lösungsmenge hier ist der Sonderfall, nämlich: , also alle Zahlenpaare mit der Eigenschaft, dass sie die Gleichung erfüllen.
8 Einsetzungsverfahren
Im ersten Teil des Einführungskurses hast du bereits gelernt, wie man ein lineares Gleichungssystem (LGS) aufstellt und es mit dem Gleichsetzungsverfahren löst. Es gibt allerdings auch andere Verfahren zur Lösung eines LGS!
Das Einsetzungsverfahren ist sehr ähnlich zum Gleichsetzungsverfahren.
Warum benutzt man das?
Ganz einfach, es ist weniger Arbeit als das Gleichsetzungsverfahren!
Wie geht das?
Beim Einsetzungsverfahren geht man so vor:
Nur eine der beiden Gleichungen nach einer der beiden Variablen auflösen.
Die Variable, nach der du aufgelöst hast, in die andere der beiden Gleichungen einsetzen.
Du erhältst einen Wert, den du wiederum in eine der Gleichungen einsetzt. Schon hast du die Lösung.
Klingt kompliziert? Ist es aber nicht! So sieht das aus:
9 Beispielaufgabe Einsetzungsverfahren
Schaue dir nun die Gleichungen an, die das Alter von Tinas Vater und Mutter liefern.
Löse die Aufgabe mit dem Einsetzungsverfahren:
1. Schritt: Gleichung auflösen
Welche Gleichung du nach welcher Unbekannten auflöst, ist teils "scharfer Blick", teils Geschmackssache! Hier wird die Gleichung nach aufgelöst.
2. Schritt: Setze in ein
3. Schritt: Setze m in ein
Tina weiß nun dank dir, wie alt ihre Eltern sind. Ihre Mutter ist Jahre alt und ihr Vater . Dies kannst du auch formal als Lösungsmenge aufschreiben:
.
10 Aufgaben Einsetzungsverfahren
Laden
Laden
11 Addition/Subtraktion von Gleichungen
Du kannst eine Gleichung mit einer anderen addieren. Aus diesen beiden entsteht eine neue Gleichung.
Warum ist das möglich?
Anschaulich kannst du dir jede Gleichung als eine Waage vorstellen. Jede ihrer Waagschalen repräsentiert eine Seite der Gleichung.
Die Gleichungen der Waagen lauten:
Waage 1:
Waage 2:
Anschließend legst du jeweils den Inhalt der linken Schalen und den Inhalt der rechten Schalen zusammen auf eine Waage. Die Waage bleibt im Gleichgewicht!
Mathematisch ausgedrückt sieht es so aus:
Waage 3:
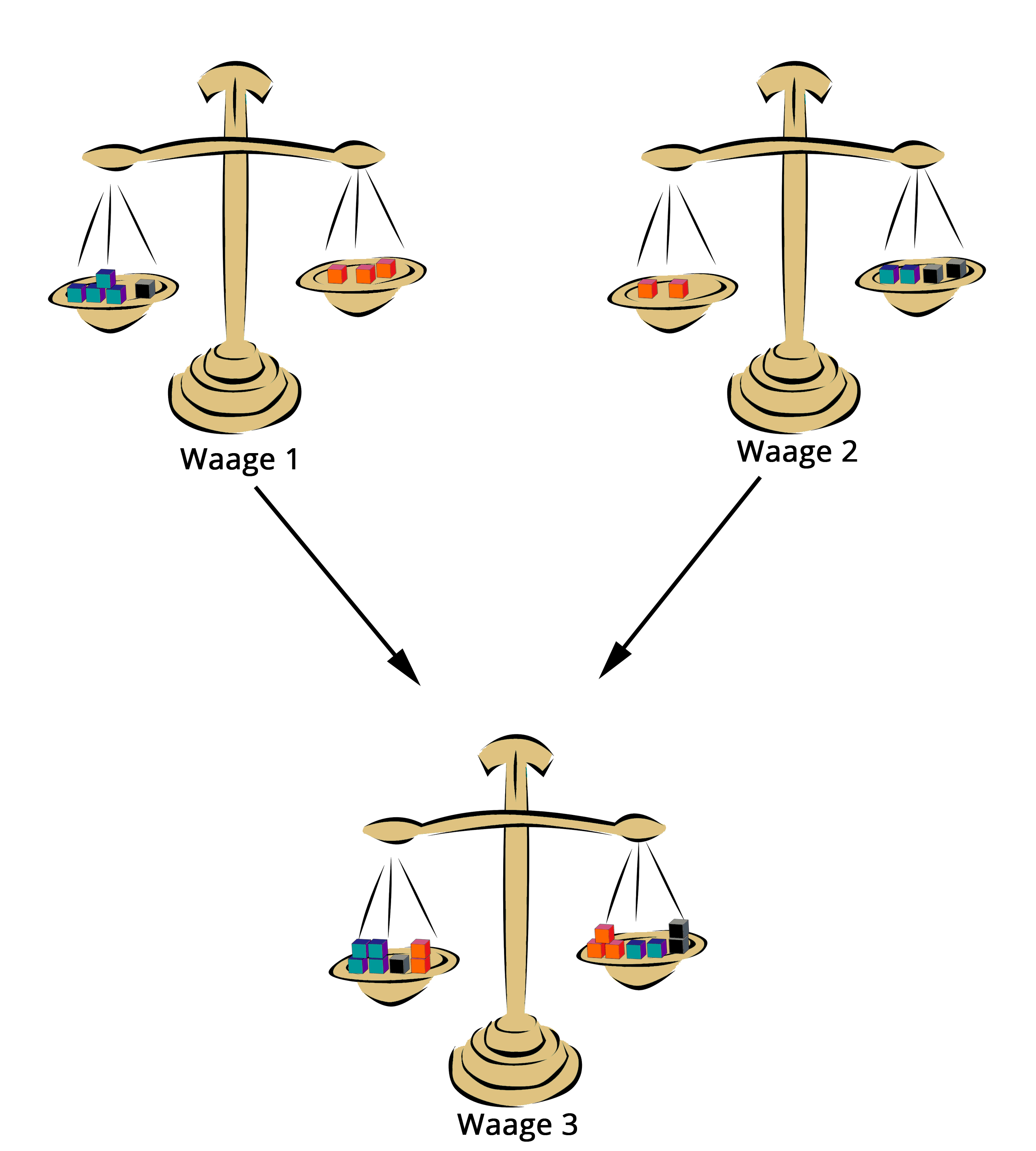
Du kannst auf die gleiche Art und Weise auch zwei Gleichungen voneinander subtrahieren.
Was passiert bei der Addition/Subtraktion von Gleichungen?
Bei der Addition/Subtraktion von Gleichungen addierst/ subtrahierst du zwei Gleichungen, aus denen eine neue Gleichung wird.
Wie bleibt allerdings die Gleichheit erhalten?
Lass dich davon nicht irritieren, dass du statt wie gewohnt Zahlen, zwei Gleichungen addieren/subtrahieren musst! Betrachte hierfür die linke und rechte Seite jeder Gleichung als einen zusammenhängenden Teil. Du gehst wie folgt vor:
Addiere/Subtrahiere die jeweiligen linken Seiten der zwei Gleichungen und fasse das Ergebnis anschließend zusammen.
Addiere/Subtrahiere die jeweiligen rechten Seiten der zwei Gleichungen und fasse das Ergebnis anschließend zusammen.
Setze zwischen der neuen linken und rechten Seite der neu entstandenen Gleichung. Die Gleichheit ist erhalten.
Es empfiehlt sich, die Gleichungen zuvor "aufzuräumen". Das heißt zum Beispiel alle Variablen (mit ihren Koeffizienten) auf die linken Seiten der Gleichungen und alle Zahlen ohne Variablen auf die rechten Seiten zu bringen.
Schwuppdiwupp hast du ganz leicht zwei Gleichungen addiert/subtrahiert, sodass daraus eine neue Gleichung entstanden ist!
Wie du diese neue Erkenntnis zur Lösung von LGS anwenden kannst, siehst du auf der nächsten Seite.
12 Additions-/Subtraktionsverfahren (1/2)
Die dritte Methode zur Lösung von LGS ist das Additions-/Subtraktionsverfahren.
Ziel dieses Verfahrens ist, eine Variable zu entfernen, indem man die Gleichungen des LGS geschickt addiert/subtrahiert.
0. Schritt: Aufräumen der Gleichungen und Auswahl der Variablen
Bringe zunächst bei deinen Gleichungen alle Unbekannten (mit ihren Koeffizienten) auf die gleiche Seite. Betrachte die Gleichungen und mit einem scharfen Blick. Ist zum Beispiel eine der Variablen in der ersten Gleichung ein ganzzahliges Vielfaches von sich selbst in der zweiten Gleichung? Wähle dann diese Variable aus.
1. Schritt: Vervielfachen der Gleichungen
In jedem Fall musst du die Gleichungen und/oder so multiplizieren/dividieren, dass die Koeffizienten der ausgewählten Variablen gleich sind (am besten dem kleinsten gemeinsamen Vielfachen entsprechend). Hierbei musst du nicht auf das Vorzeichen achten, sondern nur auf die Zahl.
13 Additions-/Subtraktionsverfahren (2/2)
2. Schritt: Entfernung einer Variablen durch Addition/Subtraktion
Fall 1: Addition der Gleichungen
Die ausgewählte Variable ist einmal mit positivem Vorzeichen und einmal mit negativem Vorzeichen in den Gleichungen und enthalten.
Addiere nun die beiden Gleichungen und wie bereits gelernt.
Fall 2: Subtraktion der Gleichungen
Die ausgewählte Variable ist zweimal mit demselben Vorzeichen in den Gleichungen und enthalten.
Subtrahiere nun die beiden Gleichungen und wie bereits gelernt.
3. Schritt: Werte der beiden Variablen bestimmen
Die neu entstandene Gleichung enthält nur noch eine Variable. Löse danach auf und finde ihren Wert heraus. Indem du nun diesen Wert in eine der beiden Gleichungen oder einsetzt, bestimmst du den Zahlenwert der anderen Variablen.
14 Beispielaufgabe Additions-/Subtraktionsverfahren (1/2)
Das Geburtstagsbeispiel wird nun auch mit dem Additions-/Subtraktionsverfahren gelöst. Das lineare Gleichungssystem dieses Problems hast du im Kurs schon gesehen:
0. Schritt: Aufräumen der Gleichung und Auswahl einer Variablen
Jetzt sind die Gleichungen aufgeräumt und du musst eine der Variablen auswählen. Dafür gibt es keine Regel.Es ist wichtig, die Variable so auszuwählen, dass die nächsten Schritte möglichst einfach sind. Du weißt: Übung macht den Meister!
Multiplizieren ist meistens einfacher als dividieren, deswegen wurde sich hier für die Variable entschieden.
In der Gleichung steht In der Gleichung steht
Man muss also rechnen.
1. Schritt: Vervielfachen der Gleichung
15 Beispielaufgabe Additions-/Subtraktionsverfahren (2/2)
2. Schritt: Entfernung einer Variablen
Jetzt stehen bei beiden Gleichungen sowohl die Unbekannten als auch die Zahlen untereinander.
Die Vorzeichen von sind unterschiedlich, also addierst du die Gleichungen.
Jetzt ist nur noch eine Variable übrig!
3. Schritt: Werte der beiden Variablen bestimmen
Löse zunächst die Gleichung aus Schritt 2 auf
Setze in eine der beiden Gleichungen ein
Zum Beispiel eingesetzt in :
Erneut gilt also: Die Mutter ist 40 Jahre alt, der Vater 45 Jahre!
.
16 Aufgaben Additions-/Subtraktionsverfahren
Laden
Laden
17 Wann benutzt man welches Verfahren?
Gleichsetzungsverfahren
Das Gleichsetzungsverfahren ist sinnvoll, wenn bereits beide Gleichungen nach der gleichen Variablen aufgelöst sind oder du beide Gleichungen leicht nach der gleichen Variablen auflösen kannst.
Einsetzungsverfahren
Das Einsetzungsverfahren ist sinnvoll, wenn bereits eine Gleichung nach einer Variablen aufgelöst ist oder leicht nach einer Variablen aufgelöst werden kann. Du kannst sie somit leicht in die andere Gleichung einsetzen.
Additions-/Subtraktionsverfahren
Das Additions-/Subtraktionsverfahren solltest du benutzen, wenn in beiden Gleichungen die gleiche Variable mit dem gleichen Koeffizienten vorliegt (z. B. in beiden Gleichungen ). Anhand des Vorzeichens entscheidest du, ob du addieren oder subtrahieren musst.
18 Zusammenfassung
Lösungsmenge
Anzahl der Lösungen
Ein lineares Gleichungssystem kann keine, eine oder unendlich viele Lösungen haben.
Wdh: Gleichsetzungsverfahren
0. Schritt: Auflösen beider Gleichungen nach einer Variablen. 1. Schritt: Gleichsetzen der beiden anderen Seiten. 2. Schritt: Auflösen nach der verbliebenen Unbekannten. 3. Schritt: Erhaltenen Wert in eine der Gleichungen einsetzen.
Einsetzungsverfahren
1. Schritt: Auflösen einer Gleichung nach einer Variablen. 2. Schritt: Einsetzen in die andere Gleichung. 3. Schritt: Erhaltenen Wert in eine der Gleichungen einsetzen.
Additions-/Subtraktionsverfahren
0. Schritt: Aufräumen der Gleichung und Auswahl einer Variablen. 1. Schritt: Vervielfachung der Gleichungen. 2. Schritt: Entfernung der Variablen. 3. Schritt: Bestimmung der Werte.
19 Zeig, was du kannst!
Laden
Laden
Laden
Laden
Laden
