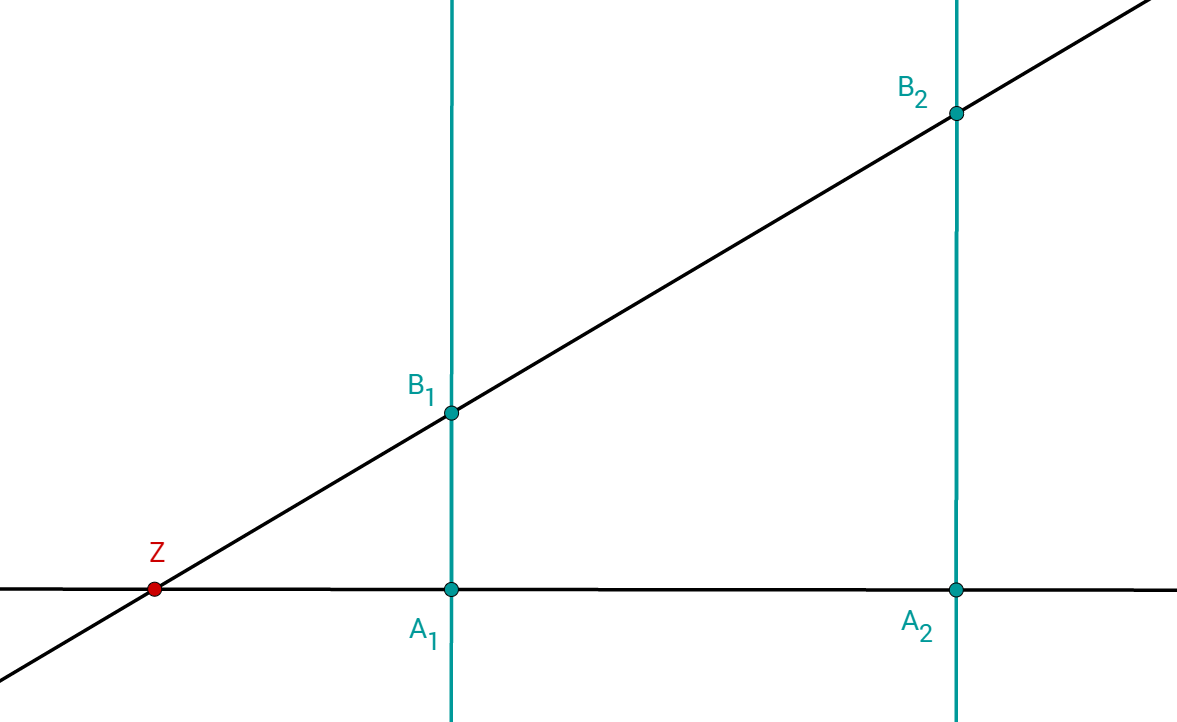
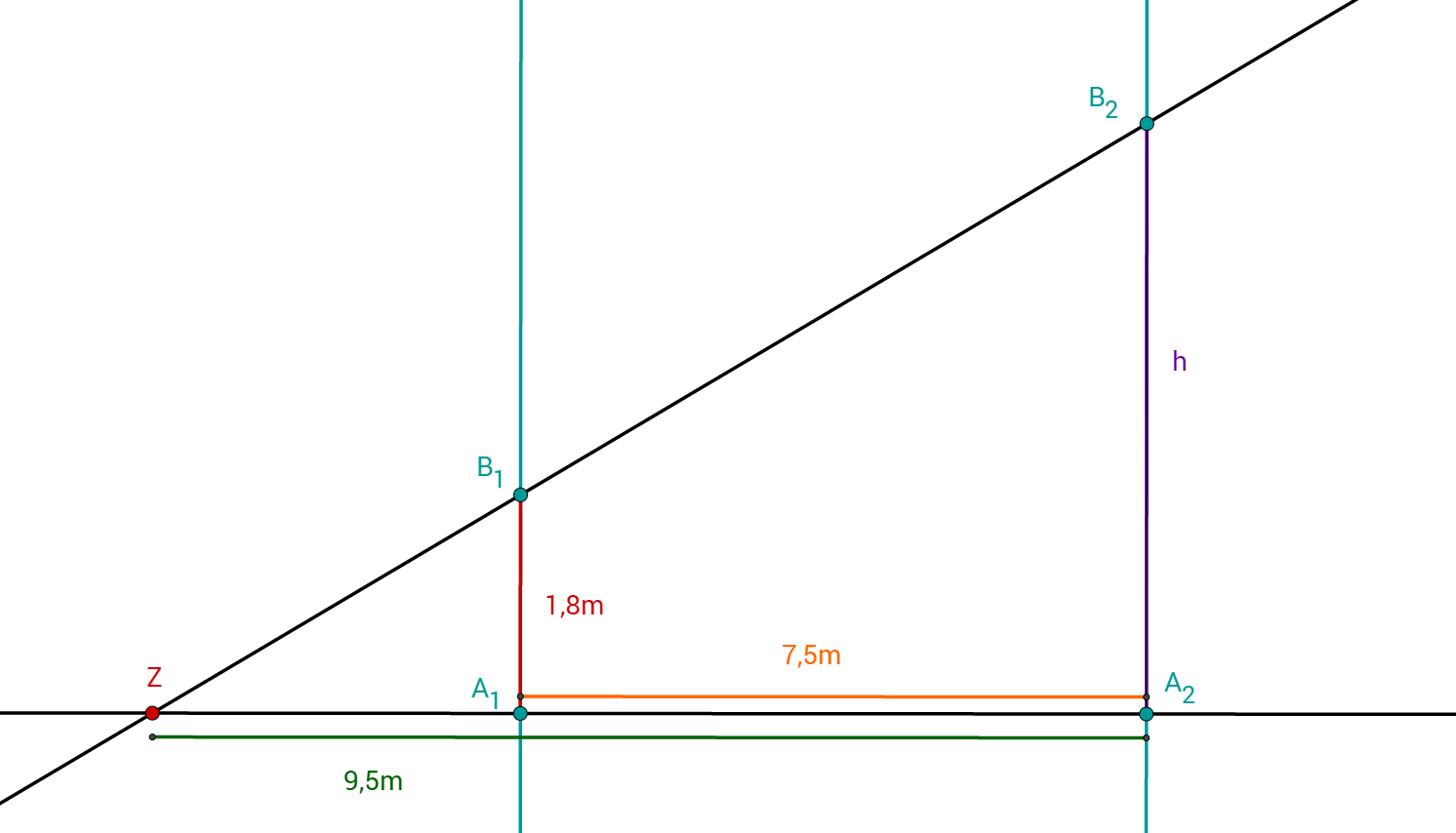
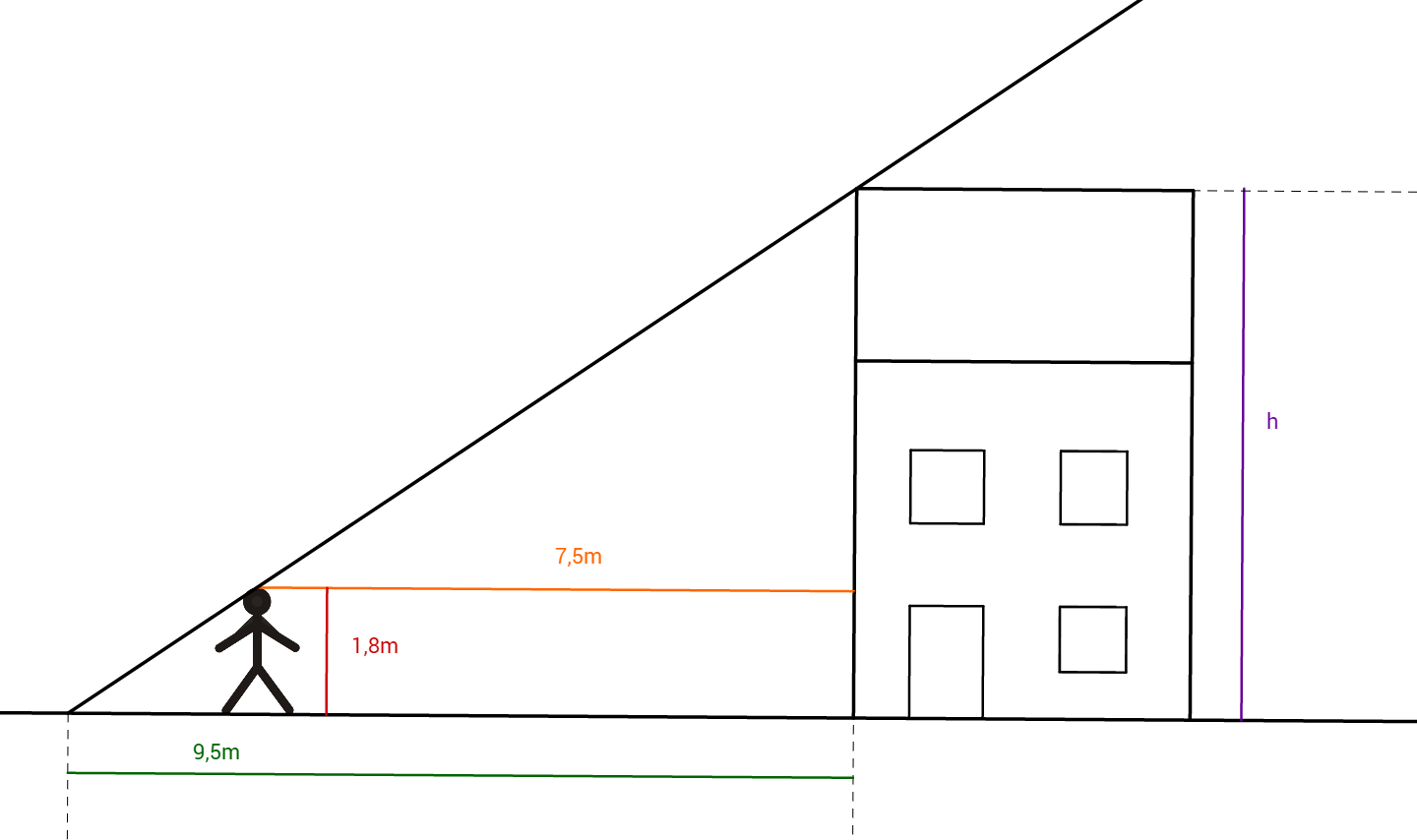
Klaus will ein Haus mithilfe des Hausschattens ausmessen. Dazu misst Klaus zuerst den Abstand vom Haus bis zum Endpunkt des Schattens. Dieser Abstand beträgt genau .
Anschließend stellt sich Klaus, der groß ist, genau an den Punkt, ab dem er im Schatten ist. Diesen Ort markiert er und misst wieder den Abstand von dieser Markierung zum Haus. Dieser beträgt .
Benutze den Strahlensatz, um die Höhe des Hauses zu berechnen!
m
